纽约金秋,海水澄澈,天空湛蓝。
午后的阳光遍洒金辉,秋风袭掠之后,始见落叶飘零。
虽然秋高气爽,心情振奋,但是寒意渐起,莫名的忧伤总是挥之不去。
学期伊始,很多新生入学,朝气蓬勃,青春洋溢。
看着他们,令老顾不禁怀念起当年入学的情形。
当时的清华园文艺气息非常浓厚,经常有各种音乐会、个人演唱会。每天夜晚东大操场上都有人在演练吉他弹唱。每天下午团委和文艺社团排练室都传来阵阵琴声,单簧管、双簧管、长笛等乐器混杂成厚重的织体,间或被长号、小号的高音所撕裂。一天傍晚,金得哲、李雪松在主楼后厅举行演唱会,他们演唱了Simon和Garfunkel的 《斯卡布罗集市》(Scarborough Fair)感人至深。歌曲旋律优美动听,歌词伤感婉约,吉他配器飘逸悠远,Simon和Garfunkel的和声浑然一体,动人心弦,堪称民谣中的经典。后来,老顾和乐队朋友郝佳良、陈皓无数次演奏过这首乐曲。郝佳良用激越嘹亮的小号吹出了醇厚柔美的感觉,陈皓单簧管的音色更是纯净无暇,令人感伤。到了博士阶段,老顾和清华乐队的朋友经常在麻省理工排练,曾经用高音萨克斯来演奏“Scarborough Fair”,但总觉得Soprano Saxophone华丽绚烂的音色,无法表达这首乐曲所蕴藏的怅惘和忧伤。再后来,老顾到纽约工作,经常到中央公园游览。Simon和Garfunkel曾经分道扬镳,后于1981年复合,在中央公园举行了一场免费音乐会。在夕阳西下、皓月初升之际,这对搭档再次演唱了这首老歌,成为永恒。
“Scarborough Fair”一唱三叹,每句歌词之后,都要加上一句叹惋“Parsley,Sage,Rosemary and Thyme”,翻译过来就是“荷兰芹、鼠尾草、迷迭香和百里香”,四种香料的名称,这令老顾大惑不解。后来,老顾游览Scarborough fair的所在地,英格兰的约克郡。和纽约(New York)相比,具有两千年历史的约克郡(old York)古老阴郁,历史文化极其厚重。这里的惠特比修道院(Whitby Abbey)是吸血鬼的诞生地;约克大教堂(York Minister)是北欧最大的哥特式教堂,具有多层地基。历史上罗马人、诺曼人、维京人、盎格鲁-萨克逊人曾经多次征服过这片土地,他们摧毁被征服者的教堂,在原址上重建自己的教堂。斯卡布罗集市曾经是北欧海盗维京人敛财销赃的据点,游吟诗人在集市上即兴创作,脍炙人口的民谣流传下来,从而启迪了保罗西蒙和葛芬柯。老顾询问当地的一位教授朋友,“荷兰芹、鼠尾草、迷迭香和百里香”的含义。教授朋友给老顾解释了一段惨痛的历史掌故。1347年,穆斯林和热那亚的基督徒殖民者之间爆发了战争。战争中,穆斯林军队爆发了黑死病。穆斯林军将病者装上了弹射器,投射到热那亚城中。恐惧的热那亚人逃回了意大利,引发了全欧洲的瘟疫。黑死病夺去了欧洲几乎一半的人口,使得人们对教会和信仰大失所望。瘟疫中却有一群盗徒穿行于死亡遍布的街市,大肆偷盗。当他们被逮捕后交待了抵御瘟疫侵袭的秘方,其中主要的成分就是荷兰芹、鼠尾草、迷迭香和百里香。由此,历史上留下了“四贼醋”的大名:Parsley,Sage,Rosemary and Thyme。由于瘟疫的恐怖,人们用将这一秘方广泛传播,演化成民谣中起兴的咒语。“Scarborough Fair”的歌词居然有如此惨烈的文化背景,民族战争,宗教战争,瘟疫黑死病,宗教改革,难怪有一种难以名状的哀伤和凄美。数百年之后,这些历史的伤痕被岁月抚平,惨痛的记忆被转化成优美的旋律和典雅的歌词。虽然人类文明提升到了古人难以想象的高度,医疗日益发达,科学日益昌明,但是宗教战争、全球性瘟疫的阴影依然挥之不去。
老欧洲的文化传统中,最为纯粹和厚重的当属数学。人类几乎出于先天的本能就会欣赏音乐。对于数学的品鉴却需要长期的专业训练。但是从带给人们的美学价值和精神震撼程度而言,数学更为崇高、激烈和持久。自从法国数学家蒙日在十八世纪初叶开启了最优传输理论的研究,数百年来无数的纯粹数学家、应用数学家、计算机科学家、工程师都为这一理论而心醉神迷,从各个角度为这一理论的发展做出了贡献。纯粹数学家证明了解的存在性、唯一性和正则性;应用数学家设计迭代格式,证明收敛阶,误差估计,数值稳定性;计算机科学家设计数据结构,并行算法,提高算法鲁棒性和效率;工程师用来进行图像增强,病理分析,统计推断,生成模型,设计光学器件等等。由于社会分工和职业训练,很少有人能够透彻理解这一理论上下游的全景,只能专注于相对局限的一部分理论或算法。例如纯粹数学家呕心沥血发展出来的各种先验估计的技巧,对于绝大多数的计算机科学家而言无法直接应用,因而缺乏动力去钻研,由此也错过了领略深层次美感的机会。近期,由于最优传输理论日益成为
深度学习的理论基础
之一,整个社会对于最优传输理论的学习热情日益高涨,相信
最优传输理论
和蒙日-安培方程理论会逐渐深入人心,在工程医疗领域发扬光大。
最优传输映射在度量空间,特别是黎曼流形上依然存在,但是其正则性分析相对困难。球面上的最优传输理论比较成熟,但是目前在工程领域应用不多。相信依随三维打印技术的成熟,球面最优传输理论终将大放异彩。这里,我们讨论球面最优传输理论的一个经典应用:由曲率来构造曲面,即凸几何中的Weyl problem,Minkowski problem和Alexandroff problem。
由微分几何的经典理论,三维空间中的曲面由第一基本形式(黎曼度量)和第二基本形式共同决定。黎曼度量决定了曲面的内蕴几何,可以测量曲面上曲线的长度,曲线间的夹角,区域的面积,同时也决定了曲面的高斯曲率。第二基本形式决定了曲面的主曲率,平均曲率。但是对于凸曲面而言,仅仅黎曼度量就决定了曲面在三维空间中的嵌入。
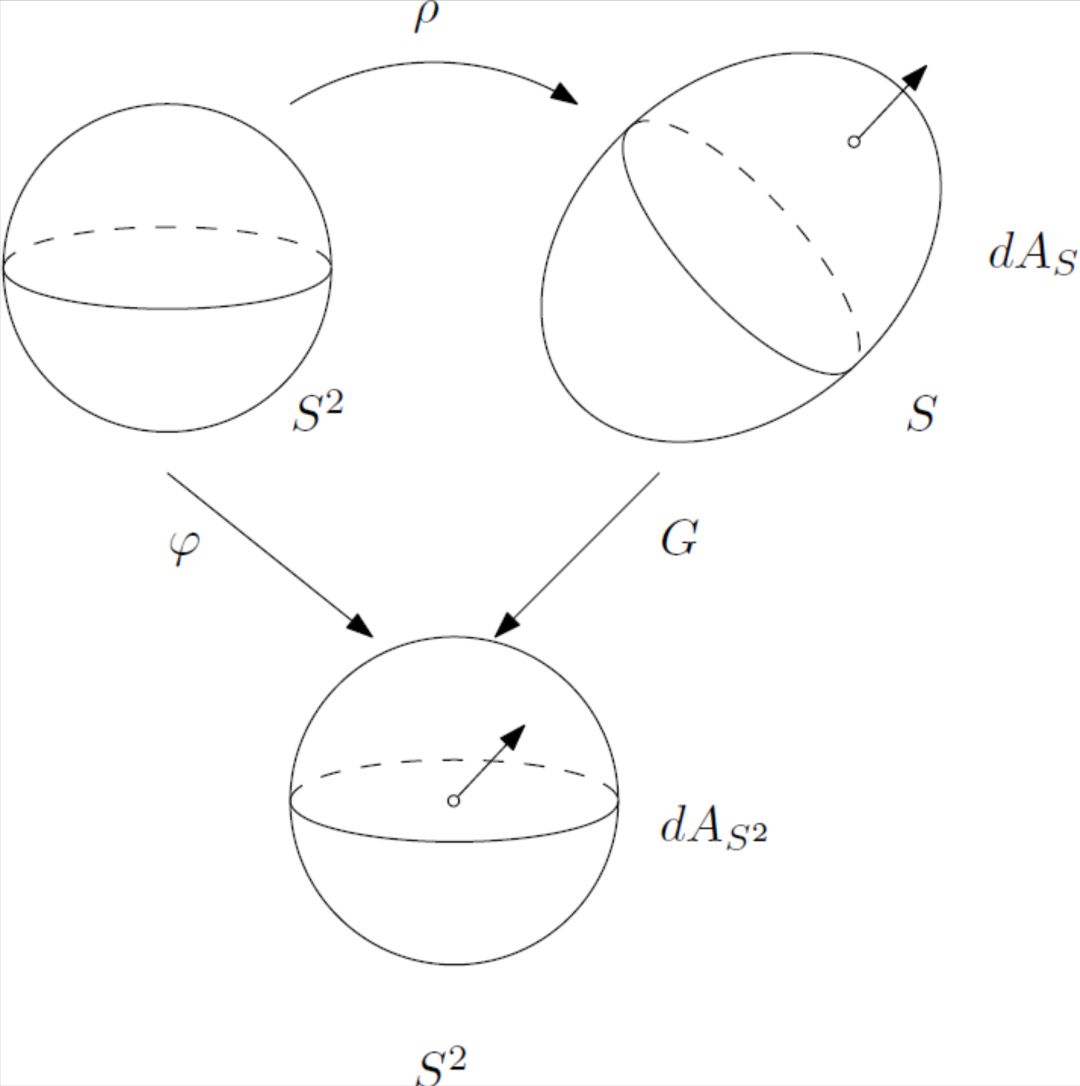
图1:源球面,高斯球面,凸曲面。
我们记凸曲面为
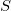 ,并且用极坐标来表示凸曲面,
,并且用极坐标来表示凸曲面,
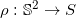 , 即用定义在单位球面上的正值函数来表达径向长度
, 即用定义在单位球面上的正值函数来表达径向长度
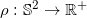 。令
。令
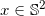 是单位球面上的一点,沿着
是单位球面上的一点,沿着
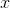 方向的射线和凸曲面
方向的射线和凸曲面
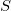 交于点
交于点
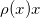 。假设曲面在点
。假设曲面在点
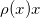 处的单位法向量为
处的单位法向量为
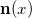 ,高斯映射将曲面映射到单位球面上:
,高斯映射将曲面映射到单位球面上:
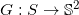 ,
,
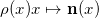 。我们将曲面的黎曼度量记为
。我们将曲面的黎曼度量记为
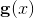 ,将曲面的高斯曲率记为
,将曲面的高斯曲率记为
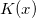 ,单位球面上的面元记为
,单位球面上的面元记为
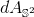 ,曲面上的面元记为
,曲面上的面元记为
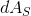 。从参数单位球面(源域)到高斯单位球(目标域)的映射为复合映射:
。从参数单位球面(源域)到高斯单位球(目标域)的映射为复合映射:
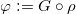 ,
,
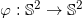 。我们下面解释下面的几个经典问题。
。我们下面解释下面的几个经典问题。
Ricci 流
:给定带有黎曼度量的曲面
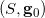 ,
给定目标高斯曲率
,
给定目标高斯曲率
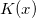 ,满足高斯-博纳条件,
则存在共形因子函数
,满足高斯-博纳条件,
则存在共形因子函数
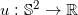 ,满足
,满足
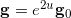 ,这里
,这里
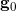 是曲面的初始度量,黎曼度量
是曲面的初始度量,黎曼度量
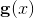 诱导曲率等于
诱导曲率等于
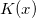 。
这里未知的共形因子函数可以由经典的Ricci流方法得到。
离散曲面Ricci流的理论和算法也非常成熟。
因此,从曲率求度量的计算问题应该已经是被完全解决了。
但是,我们只得到黎曼度量,有时需要进一步得到曲面在欧式空间中的等距嵌入或者浸入。
。
这里未知的共形因子函数可以由经典的Ricci流方法得到。
离散曲面Ricci流的理论和算法也非常成熟。
因此,从曲率求度量的计算问题应该已经是被完全解决了。
但是,我们只得到黎曼度量,有时需要进一步得到曲面在欧式空间中的等距嵌入或者浸入。
Minkowski问题
:我们在目标域高斯球上给出高斯曲率,即给定高斯球上的任意一点
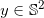 ,相应的正值高斯曲率为
,相应的正值高斯曲率为
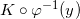 ,满足条件
,满足条件
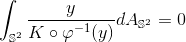 ,
,
求取曲面的极坐标表示
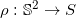 。等价的,高斯映射将曲面的面元推前到高斯球面上,在高斯球面上得到一个测度
。等价的,高斯映射将曲面的面元推前到高斯球面上,在高斯球面上得到一个测度
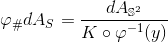 ,
,
从这一推前测度来求取凸曲面。
从计算角度而言,这一问题可以如下求解。首先我们将Minkowski问题离散化。我们将高斯球进行胞腔分解,
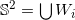 ,计算积分
,计算积分
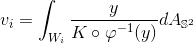 ,
,
令法向量为
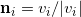 ,面积为
,面积为
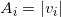 ,满足限制
,满足限制
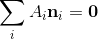 ,
,
我们欲求一个凸多面体,相应面的法向量为
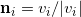 ,面积为
,面积为
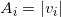 。
。
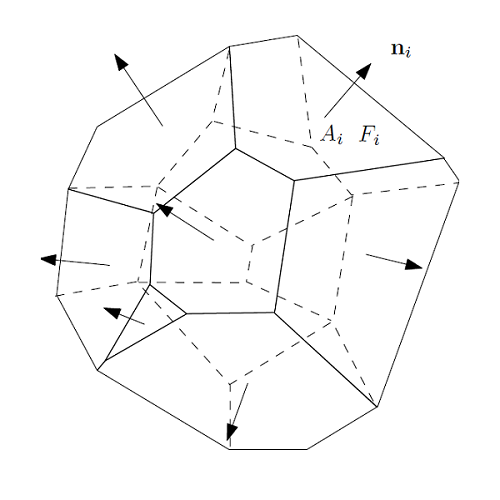
图2:离散Minkowski问题。
这里凸多面体的支撑平面方程为
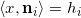 ,这里平面的高度
,这里平面的高度
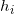 未知。这些支撑平面构成的凸多面体记为
未知。这些支撑平面构成的凸多面体记为
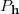 ,这里
,这里
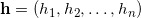 。我们构造能量函数为凸多面体的体积
:
。我们构造能量函数为凸多面体的体积
:
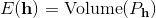 ,极大化凸多面体的体积,满足限制
,极大化凸多面体的体积,满足限制
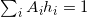 。多面体体积关于支撑平面高度的偏导数等于相应面的面积:
。多面体体积关于支撑平面高度的偏导数等于相应面的面积:
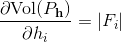 ,
,
由此可以证明离散Minkowski问题解的存在性。再由Brunn-Minkowski不等式证明解的唯一性。
我们再将高斯球的剖分逐步加细,得到一系列的凸多面体,从中选择子列收敛到光滑解。















