撰文:David Tong(剑桥大学)
翻译:素春(哈佛大学)
众所周知,几何与物理之间的关系非常密切,最出名的例子当属爱因斯坦的广义相对论:用几何上的时间和空间来描述物理上的引力。本文将试图描述大自然是如何汇入几何的。让我们用物理学中的概念从一个新的视角去看一下数学的样貌。
首先,我们需要两个简单的概念:一个来自数学,另一个来自物理。数学方面的主要概念就是流形(manifold)。如果你之前没有听说过流形,那么你可以想象一个弯曲且闭合的表面,比如一个球⚽️或甜甜圈🍩的表面,而流形就是这种形状在多维空间的推广。几何的目的就是要理解不同流形的属性,它们之间的关系,以及我们用以描述它们的语言。 而在物理方面,我们唯一需要的就是谦逊的粒子。我们的计划如下:把粒子放在要研究的流形上让它漫游。通过理解粒子的行为,我们可以推测粒子背后的空间(即流形)的各种属性。

○ 卡拉比-丘流形。 | 图片来源: Andrew J Hanson, Indiana University
让我们从最简单的情况开始,想象一个满足经典力学理论的粒子。这种经典粒子平淡无奇,它会像我们预测的一样:按照空间的轨迹滚动。经典粒子走过的轨道会满足一些特殊的数学性质,此轨道叫做测地线(geodesic)。但是这种让经典粒子运动的概念非常受限,无法用来探测流形深处的东西。而且这种经典粒子的视野非常狭隘,它只能看到它自身周围的一小块区域,却对流行的整体性质无从而知。
如果我们转向量子力学,事情会变得更加有趣。在量子世界里,粒子不再拥有一个确定的位置,事情会变得更加不确定,我们需要用概率的语言来描述。在量子力学中,粒子是用数学上的波函数 ψ(x) 来描述的。波函数是一个复数函数,而x是一系列坐标,用以标记流形上的各个点。粒子在x点的概率正比于 |ψ(x)|²。量子粒子以概率波的形式散开其实给了它更强大的能力。这让量子粒子能感受到它在整个流形上的轨迹(相比之下,经典粒子只能看到它自身周围的一小块区域)。它由此可以得知空间的整体结构。量子粒子的态是由薛定谔方程来描述的:

这个符号 叫做拉普拉斯算子。粗略的说,它表示你需要把 ψ 相对于所有的相关自变量做二阶微分。一般情况下,大家第一次见到拉普拉斯算子应该是相对于平直的三维空间
叫做拉普拉斯算子。粗略的说,它表示你需要把 ψ 相对于所有的相关自变量做二阶微分。一般情况下,大家第一次见到拉普拉斯算子应该是相对于平直的三维空间  (即 x ≡ (x,y,z) )做的二阶微分,
(即 x ≡ (x,y,z) )做的二阶微分,

拉普拉斯由此平直三维空间中的形式向不同维度的扩展显而易见。但更重要的是,拉普拉斯算子也可以向弯曲的流形扩展。这种情况下,拉普拉斯算子取决于流形的度规(metric),也就是说此拉普拉斯算子符号之内已经包含了流形中不同的点之间的距离的相关信息。
在上文的薛定谔方程中,E 只是一个实数。物理学家们会把它理解为粒子的能量。这里的核心思想是薛定谔方程并不是对于任意E 值都会有 ψ(x) 解,而是只对某些特定的不连续的E值有解。而且,因为拉普拉斯算子 取决于我们在哪个空间讨论,有解的E值也一样由空间决定。这给我们提供了一个非常不同的方式去看待几何。你给我一个流形,告诉我它的形状及曲率(更确切的说,是拓扑和度规)。用这些信息,我来解薛定谔方程并给回你一列E 值。这一系列 E 值叫做拉普拉斯算子谱,其内包含流形的绝大部分信息。这种思维方式叫做谱几何(spectral geometry)。
取决于我们在哪个空间讨论,有解的E值也一样由空间决定。这给我们提供了一个非常不同的方式去看待几何。你给我一个流形,告诉我它的形状及曲率(更确切的说,是拓扑和度规)。用这些信息,我来解薛定谔方程并给回你一列E 值。这一系列 E 值叫做拉普拉斯算子谱,其内包含流形的绝大部分信息。这种思维方式叫做谱几何(spectral geometry)。
谱几何还有一个更接地气的版本。数学家 Mark Kac 曾在《我们能否听到鼓的形状?》一文中提到此版本而让它闻名于世。鼓震动的频率也是遵循薛定谔方程的,只不过此时要满足一个特殊的边界条件:由鼓的边缘形状而定。现在的问题是:如果你已知所有的频率,你能反推出鼓的形状吗?答案是不能,但是你可以由此得到很多鼓的形状的相关信息。相似的,在几何学中大家都知道谱的信息未必足以推测出背后的流形的所有信息。然而,谱几何仍是一个内容丰富的学科,谱中以非常有趣的形式嵌含了流形的各种不同属性。
为了帮助我们更好的理解谱几何,我们一起来看一个非常简单的流形的例子:圆。让我们用维度x标记沿圆周的位置。假设圆的半径为R,我们可知 x ≡ x + 2πR 在此例中,薛定谔方程非常简单,即

薛定谔方程的解也非常简单,即 ψ = exp(inx/R)。此时,“我们所研究的空间是一个圆”的信息体现于这一要求:ψ 在圆周上的任一点都只有单一的值,所以ψ(x) = ψ(x+2πR)。由此可知我们必须有 ,而此圆(一个简单的流形)的谱则是一个数字塔
,而此圆(一个简单的流形)的谱则是一个数字塔

我们很快还会回头再看这个圆的例子。
虽然我是从量子物理的角度来介绍谱几何,但谱几何学科并非由物理学家发现。不过,值得开心的是谱几何可以如此自然的融于量子物理的框架中,而且这二者之间还有更多的关联。比如,一个更加复杂的拥有超对称性质的量子力学哈密顿量可以很自然的捕捉到流形的德拉姆或者多尔贝上同调。这样,很多微分几何的伟大结果就可以用量子物理的语言重述了。这个方向非常有趣,但不在本文讨论范围之内。本文的重点是要告诉你一些用物理的语言思考几何时会得到的一些新奇东西。
弦论是我们目前所知的能统一引力和量子力学的一个最好的假说理论。弦论的基本概念表面上看起来有些愚蠢:它说在最基础的层面,如果你深深的看入每一个粒子,你将会看到一个小小的振动的弦圈。目前,弦论尚无实验证据支持。然而,弦论是一个很强大的数学框架。现在我们就拿这个框架来解释一些几何上的问题。我们依旧用之前用过的同样策略,问这样一个问题:一个在流形上运动的弦的能量谱是什么样的?
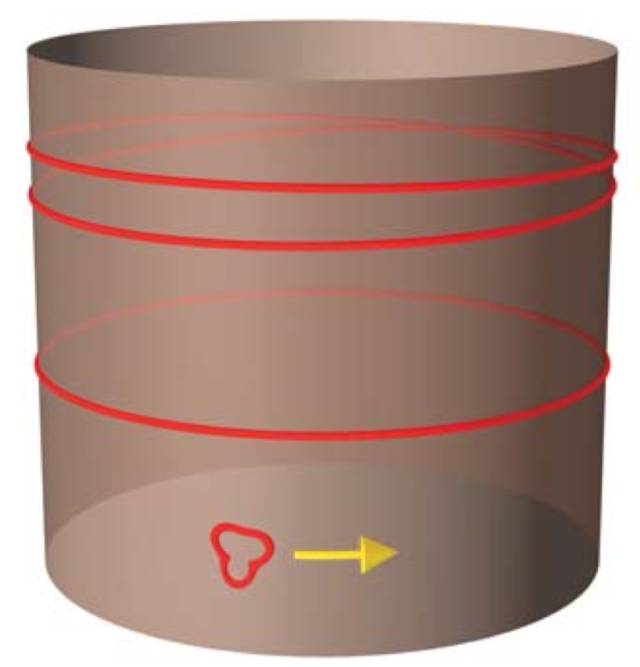
○ 弦的行为。 | 图片来源: Steuard Jensen, Alma College
让我们回到圆的例子中。现在弦可以做两件不同的事情。第一,弦可以形成一个小圈然后绕着圆运动。因为,从远处看来,这个弦圈就是一个粒子,显然此弦圈的能量谱应该跟粒子的能量谱一样,即: 。但是弦还可以做一些粒子做不到的事情:它可以拉伸自己。你可把弦想象成一条橡皮筋;拉伸需要能量,而如果一条弦绕着圆绕了 m 圈,它将会拥有的能量
。但是弦还可以做一些粒子做不到的事情:它可以拉伸自己。你可把弦想象成一条橡皮筋;拉伸需要能量,而如果一条弦绕着圆绕了 m 圈,它将会拥有的能量  。这说明绕圆运动的弦的能量谱包含了两个数字塔:
。这说明绕圆运动的弦的能量谱包含了两个数字塔:

这儿有一件非常有意思的事。如果我们把 R 和 1/2πR 互相代换(如下面式子所示),这一系列能量谱将会保持不变。

这说明,如果你得到的只是一个能量谱,你根本无法判断这个流形圆是一个半径为 R 的大圆还是一个半径为 1/2πR 的小圆。从弦的视角来看,这两个圆看起来一模一样!当然,我们此处只是讨论了弦的能量谱,但其实弦的所有属性都是可以遵循上面式子中的交换而保持不变的。弦真的是不能区分大圆和小圆的。这是一个美丽的事实,它的名字却非常朴实无华:T 对偶(T-duality)。
弦的迷惑不仅存在于圆这个简单的例子中,也延伸到了其他的流形中。粗略的说,流形总是成对存在的。虽然从粒子的角度来看,这样一对中的两个流形是非常不同的,从弦的角度看来,这一对中的俩流形可是一模一样的。(此结论对于一类特殊的叫做卡拉比-丘的流形是绝对正确的,而对于其他的流形还有一个稍微扩展的版本)。但是这两个流形之间的关系并不是如大圆小圆那种简单关系。相反的,这两个流形第一眼看上去并不相关。大部分时候,它们甚至连拓扑性(即流形上的洞的数量,如甜甜圈有一个洞)都不同。
这种流形之间的成对性叫做镜面对称(mirror symmetry)。弦不能区分这两个流形其实反而是弦的一大优点。首先,我们知道流形之间存在非常奇怪且难以预测的关系。而且,数学家们通常可以对其中一个流形有很多话说,却对另外一个无话可说。然而,依照弦论,这两个流形是一样的;你只是需要用一个正确的方式去看它们。关于第一个流形的任一(可以回答的)问题都可以告诉你关于另一个流形的一些有趣的事。(严格来说,所有关于第一个流形的复几何学领域的问题都可以转化为关于另一个流形的辛几何学领域的问题)。由此,镜面对称可以变成一个强大的工具让我们通过研究配偶流形的方法来探索我们以前不理解的一些流形。
镜面对称是25年前发现的。那时候,镜面对称成为几何中最火热的研究领域之一,吸引了大批数学家和物理学家。我们需要承认,数学和物理的研究方式有所不同。物理学家倾向于不死磕严密性上,而是更依赖于一些直观景象来理解大自然该怎样在一个推测的基础之上建立另一个推测。当然,数学家们在一个推测得到严格证明前是不会满足的。镜面对称是少有的但是数量正在增长的数学家和物理学家手拉手探索同一个问题的领域之一。这种友好合作关系给数学界和物理界都带来了繁荣。
本文经理论物理学家David Tong教授授权翻译转载,
原文链接:http://www.damtp.cam.ac.uk/user/tong/talks/geomphysics.pdf














