Here’s a popular s
tory about momentum
[1, 2, 3]
: gradient descent is a man walking down a hill. He follows the steepest path downwards; his progress is slow, but steady. Momentum is a heavy ball rolling down the same hill. The added inertia acts both as a smoother and an accelerator, dampening oscillations and causing us to barrel through narrow valleys, small humps and local minima.
This standard story isn’t wrong, but it fails to explain many important behaviors of momentum. In fact, momentum can be understood far more precisely if we study it on the right model.
One nice model is the convex quadratic. This model is rich enough to reproduce momentum’s local dynamics in real problems, and yet simple enough to be understood in closed form. This balance gives us powerful traction for understanding this algorithm.
We begin with gradient descent. The algorithm has many virtues, but speed is not one of them. It is simple -- when optimizing a smooth
function
f
, we
make a small step in t
he gradient
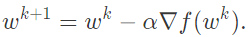
For a step-size small enough, gradient descent makes a monotonic improvement at every iteration. It always converges, albeit to a local minimum. And under a few weak curvature conditions it can even get there at an exponential rate.
But the exponential decrease, though appealing in theory, can often be infuriatingly small. Things often begin quite well -- with an impressive, almost immediate decrease in the loss. But as the iterations progress, things start to slow down. You start to get a nagging feeling you're not making as much progress as you should be. What has gone wrong?
链接:















