基础准备
前面草堂君给大家详细介绍适用于不同场景和数据类型的相关系数类型,以及如何使用统计软件对它们进行计算,大家可以点击下方文章链接进行回顾:
今天草堂君给大家介绍的相关系数类型是在问卷分析中经常会用到的一种可靠性指标,特别是在跨层的问卷分析研究中会用到,它就是组内相关系数ICC(Intraclass Correlation Coefficients)。在跨层研究中,ICC决定了个体层面的数据是否能够转换成团体层面的数据,以及是否需要在跨层次研究中区分组间效应和组内效应。跨层研究的内容将会在后面介绍Mplus软件时再详细介绍。
ICC系数
在很多需要通过实验测量来获取实验数据的分析中,都会包括实验误差,这些实验误差会导致很多不可靠的分析结论。正因为如此,经常需要对实验数据的变动进行分解,搞清楚引起数据变动的因素有哪些,以及每个因素引起的变动占总变动的比例。如果随机误差在数据总变动中所占的比例很高,说明数据结果是不可靠的。
ICC是组内相关系数(IntraclassCorrelation Coefficients)的缩写,用来描述同一个组内的数据的相似性,这里的组可以是一组题目,也可以是一组打分者,或者其它分析者感兴趣的对象。通常情况下,组内相关系数表示为组内方差除以总方差,因此,组内相关系数越高,说明随机误差占比越小,代表同一组数据之间的相关性越强。
组内相关系数有六种类型,如下所示:
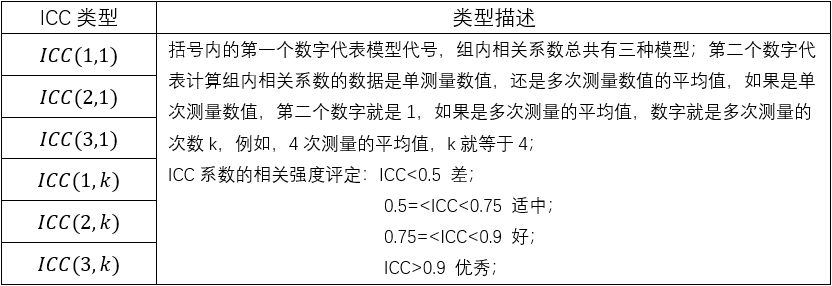
ICC的三个模型六种系数
组内相关系数经常用于评分者信度研究和测量工具可靠性研究。下面以评分者信度研究为例,说明ICC系数的三种分析模型。现在我们假设,在评分者信度研究中,让k个评分者对n个目标物(打分对象或量表题项)打分(例如,k个裁判对n个歌手的表现进行打分;k个评卷老师,对n个学生的试卷进行判定),那么会有以下三种情况,对应六种组内相关系数的模型。
另外,组内相关系数,需要明确分析的是谁的组内相关系数。上面的例子中,可以分析n个题目的组内相关系数,也可以分析k个评分者的组内相关系数。分析谁的组内相关系数,在后面的系数计算公式中,分子就放谁的方差。
模型一
假设有n个目标物,每个目标物(量表题项)都由从总体中随机抽取的k个评分者打分,例如,总共n道题,每道题都随机从一群人中抽取k个进行打分,如下表所示:

在这种情况下,每道题的每个分数可以用下面的线性模型表示:

上方线性模型对应的分析方法是随机效应的单因素方差分析。方差分析的成分构成如下表所示,分为题项主效应和误差项:

对模型一,如果分析n个题项间的组内相关系数,ICC的计算公式为:
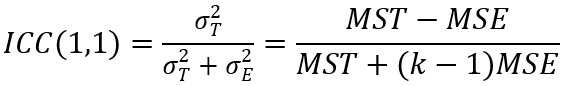
如果计算ICC系数的数据是多次测量的平均值,如下表所示,每个单元格内的数值是k次测量的平均值:

那么组内相关系数的计算公式如下所示,推导过程会在后面的文章中介绍:
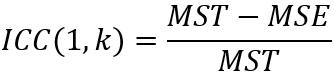
情况二
同样有n个目标物,但是只从一群打分者总体中随机抽取k人,这k个打分者需要给每个目标物打分。举个例子,总共5道题,从打分者总体中,随机抽取5个打分者,每个打分者在每道题上都进行打分。

这种情况,因为打分者是从打分者总体中随机抽取的k个人,这k个人对每个目标物都进行打分,因此需要考虑打分者主效应了,可以列出线性模型:

上方有交互作用的两因素随机效应方差模型的成分构成如下:


情况三
第三种情况与第二种情况类似,不同之处在于k个打分者不是随机抽取的,而是特定的k个打分者。例如学校里的小型考试,批改试卷的老师就那么几个人,而无法随机选择老师进行批改。线性模型与第二种情况一样,如下所示,区别在于后面讲述的效应方差不同。

上方有交互作用的两因素混合效应方差模型在形式上虽然与第二种情况的模型一样,但是它们的方差成分构成却不同:


从以上介绍内容可知,上面三种情况的方差分解结果是不一样的。第一种情况的模型称为单因素随机效应方差模型;第二和第三种情况的模型称为有交互的两因素方差分析模型,区别在于第二种情况的有交互两因素方差分析模型中,题项和打分者的主效应都是随机效应,而第三种情况中,题项主效应是随机效应,而打分者主效应是固定效应。前面草堂君介绍过固定效应的方差分析模型(回顾:数据分析理论:方差分析模型),随机效应和混合效应的方差分析模型后面草堂君会再详细介绍。
案例分析
现在有一份4个打分者对6个题项的打分数据,数据结构如下表所示:

将上方数据整理成spss软件格式,结果如下图所示:
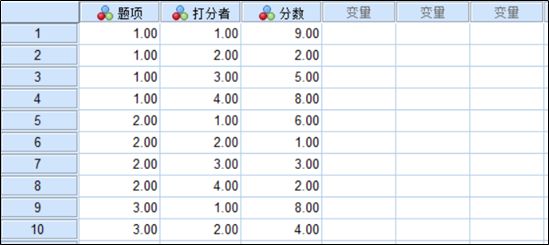
(可前往qq群:577312904和134373751下载案例数据)
分析思路
今天草堂君首先介绍用方差分析的结算结果来计算ICC系数。因为SPSS软件中有特定的计算ICC系数的菜单,下篇文章,草堂君将介绍用固定菜单计算ICC系数,大家可以将两次计算过程和结果进行对比,充分了解ICC系数。
情况一ICC系数分析过程
1、点击SPSS软件菜单【分析】-【一般线性模型】-【单变量】,跳出下方菜单。因为只有题项是随机因子,所以将题项变量选为随机因子,分数选为因变量。
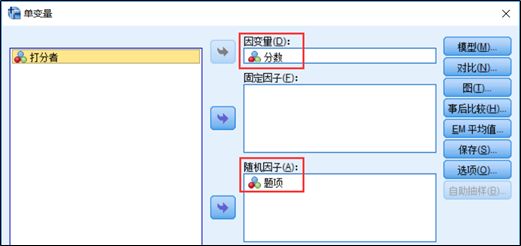
2、结果解释。经过上述操作,输出下方分析结果。从结果可知,题项主效应对应的均方MST为11.242,而误差项的均方MSE为6.264。
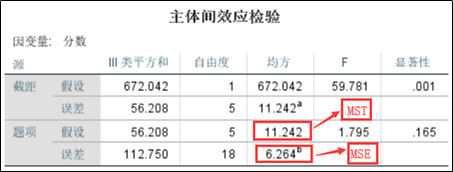

情况二ICC系数分析过程
1、点击SPSS软件菜单【分析】-【一般线性模型】-【单变量】,跳出下方菜单。因为题项和打分者都是随机变量,所以,操作方式按下图进行,将题项和打分者变量选为随机因子,点击模型按钮,选择构建项,然后在类型中选择主效应,将题项和打分者选入模型。
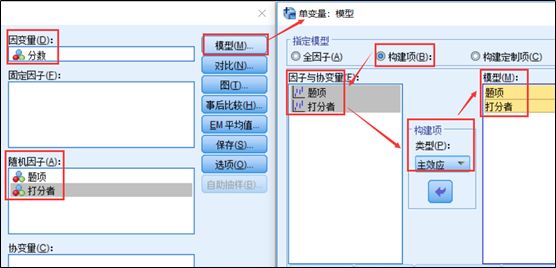
2、分析结果。从分析结果可知,题项主效应的均方MST等于11.242,打分者主效应的均方MSD为32.486,误差项均方MSE等于1.019。
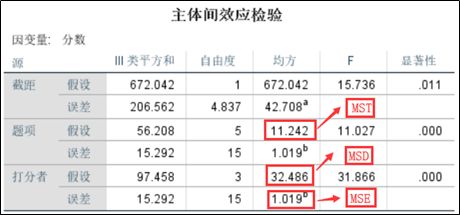

情况三ICC系数分析过程
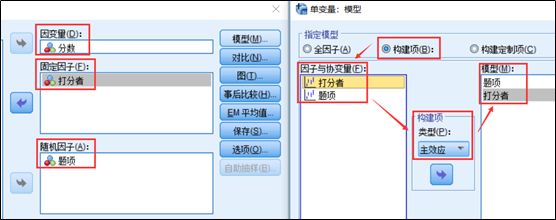
1、点击SPSS软件菜单【分析】-【一般线性模型】-【单变量】,跳出下方菜单。因为题项是随机变量,而打分者是固定变量,所以,操作方式按下图进行,将题项选为随机因子,打分者选为固定因子,点击模型按钮,选择构建项,然后在类型中选择主效应,将题项和打分者选入模型。
2、分析结果。从分析结果可知,题项主效应的均方MST等于11.242,打分者主效应的均方MSD为32.486,误差项均方MSE等于1.019。可以发现,结果和上面情况二是一样的。区别在于每个项的含义变化了。



















