烧脑！CMU、北大等合著论文真的找到了神经网络的全局最优解

点击上方蓝色字体，关注我们

来源：机器之心

一直以来，我们都不知道为什么 深度 神经网络 的损失能降到零，降到零不代表着全局最优了么？这不是和一般 SGD 找到的都是局部极小点相矛盾么？最近 CMU、北大和 MIT 的研究者分析了深层全连接网络和残差网络，并表示使用 梯度下降 训练过 参数 化的 深度 神经网络 真的能找到全局最优解。

用一阶方法训练的 神经网络 已经对很多应用产生了显著影响，但其理论特性却依然是个谜。一个经验观察是，即使优化 目标函数 是非凸和非平滑的，随机初始化的一阶方法（如随机 梯度下降 ）仍然可以找到全局最小值（训练损失接近为零），这是训练中的第一个神秘现象。令人惊讶的是，这个特性与标签无关。在 Zhang 等人的论文 [2016] 中，作者用随机生成的标签取代了真正的标签，但仍发现随机初始化的一阶方法总能达到零训练损失。

人们普遍认为过 参数 化是导致该现象的主要原因，因为 神经网络 只有具备足够大的容量时才能拟合所有训练数据。实际上，很多 神经网络 架构都高度过 参数 化。例如，宽残差网络（Wide Residual Network）的 参数 量是训练数据的 100 倍。

训练 深度 神经网络 的第二个神秘现象是「更深的网络更难训练。」为了解决这个问题， 何恺明 等人在 2016 年提出了 深度残差网络 （ResNet）架构，用随机 梯度下降 方法来训练显著具有更多层数的 神经网络 。理论上来说，Hardt 和 Ma [2016] 表明，线性网络中的残差连接可以阻止梯度消失为零，但使用非线性 激活函数 的 神经网络 还无法利用残差连接的优势。

在本文中，作者将揭开这两个神秘现象的面纱。具体而言，作者们从理论上分析了 损失函数 在 梯度下降 上的 收敛 情况，即采用全连接网络和残差网络架构下的 损失函数 收敛 情况。作者关注根据欧式距离定义的 损失函数 ，并假设 激活函数 是 Lipschitz 和平滑的。这种假设适用于很多 激活函数 ，包括 soft-plus。本文贡献如下：

首先考虑全连接前馈网络。作者表明，如果层级的 神经元 数量 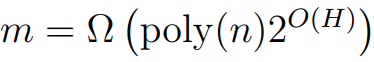，则随机初始化的 梯度下降 会以线性速率 收敛 到零训练损失。

接下来考虑 ResNet 架构。作者表明，只要中间层的宽度 m = Ω (poly(n, H))，则随机初始化的 梯度下降 会以线性速率 收敛 到零训练损失。与第一个结果相比，ResNet 对网络层数的依赖呈指数级上升。该理论阐明了利用残差连接的优势。

最后，作者利用同样的技术来分析卷积 ResNet。作者表明，如果 m = poly(n, p, H)，其中 p 是图像块数量，则随机初始化的 梯度下降 会达到零训练损失。

本文的证明是基于以前关于双层 神经网络 梯度下降 研究中的两个重要概念。第一个是 Du 等人 [2018b] 提出的概念，本文作者分析了 神经网络 预测的动力学特征，即其 收敛 性由格拉姆矩阵（Gram matrix）的最小特征值决定。为了降低最小特征值的下界，从初始化开始限制每个 权重 矩阵的距离就足够了。其次，作者利用了 Li 和 Liang [2018] 的观察结果，即如果 神经网络 过 参数 化，则每个 权重 矩阵接近其初始化。与前两个研究不同，本文在分析 深度 神经网络 时，需要构建更多 深度 神经网络 的架构属性和新技术。在本文中，我们主要介绍了 ResNet 的分析结果，更详细的证明展示在原论文中的 29 页附录中。

论文：

Gradient Descent Finds Global Minima of Deep Neural Network s

论文地址：

https://arxiv.org/pdf/1811.03804.pdf

摘要： 在训练 深度 神经网络 时，即使 目标函数 是非凸的， 梯度下降 法也能找到全局最小值。本文证明了对于具有残差连接的深度超 参数 神经网络 （ResNet）， 梯度下降 可以在多项式时间内实现零训练损失。我们的分析依赖于 神经网络 架构引入的格拉姆矩阵的多项式结构。这种结构帮助我们证明格拉姆矩阵在训练过程中的稳定性，而且这种稳定性意味着 梯度下降 算法的全局最优性。我们的边界也揭示了使用 ResNet 优于全连接前馈架构的优点；对于前馈网络，我们的边界要求每层 神经元 的数量随深度进行指数缩放，而对于 ResNet，边界只要求每层 神经元 的数量随深度进行多项式缩放。我们还进一步将自己的分析扩展到深度残差卷积 神经网络 并得到了类似的 收敛 结果。

本文结构：第二节正式介绍了问题背景；第三节给出了在深度全连接 神经网络 上得到的主要结果；第四节给出了在 ResNet 上得到的主要结果；第五节给出了在卷积 ResNet 上得到的主要结果；第六节为以上三种架构提供了一个统一的证明策略。第 7 节为总结，证明见附录。

在论文的后面的章节中，大部分都在描述假设与推理。尤其在后面 29 页的附录中，作者给出了各推理的完整的证明。如果读者自信数学底子比较硬朗的话，可以查阅原论文了解详细推导过程，本文后面只简要介绍了 ResNet 的分析结果。

ResNet 的主要分析结果

在这一章节中，作者主要会考虑使用 梯度下降 训练 ResNet 的 收敛 性，并关注到底需要多大程度的过 参数 化才能确保 梯度下降 收敛 到全局最优解。当然在这之前需要明确 ResNet 的形式化定义是什么样的。在这篇论文中，作者们主要分析了不同 神经网络 的经验风险最小化问题，其中 损失函数 由一般的欧式距离定义：

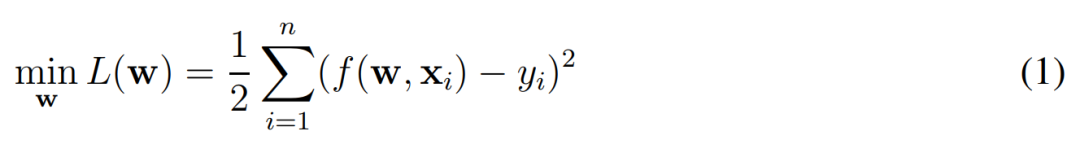
这个式子很容易理解，w 是 神经网络 所有的 权重 ，x 为输入样本（如图像）、y 为样本的对应标注。在实践中，f(w, x_i) 表示的就是一个完整的残差网络（ResNet），我们希望利用 梯度下降 一步步调整 ResNet 中的 权重 w，进而获得经过训练的 ResNet。从形式化上来说，ResNet 或 f(w, x_i) 函数可以表示为如下方程式：

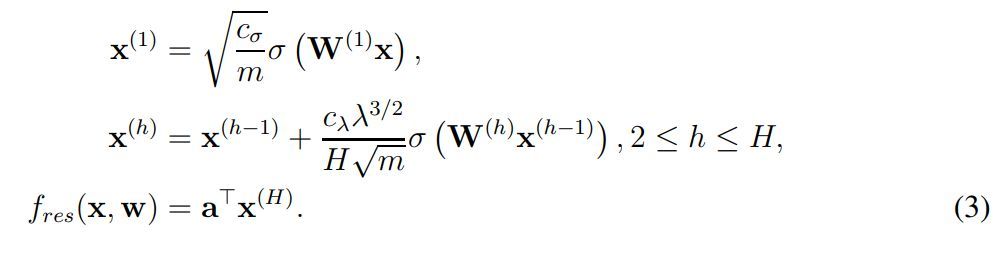
其中 x^(1) 表示输入图像 x 经第一个卷积层得出的特征图（feature map），c_σ为初始化阶段中归一化输入的缩放因子，这里并没有详细展示 c_σ的表达式，详情可查看原论文。此外，σ表示一般的 激活函数 ，且作者假设算出来的中间层（x）都是方阵。在 x^(h) 中，作者形式化定义了残差第 h 个残差模块的输出，它会通过残差连接将 h-1 层的输出加上当前层的输出。x^(h) 后面σ左边比较复杂的表达式展示了这一层级的缩放因子，它们具体是什么可以查阅原论文。

最后的 f_res(x, w) 则表示了残差网络的最终表达式，即最后一个残差模块的输出做一个简单的反射变换。因此为了分析 ResNet 的 收敛 情况，作者定义了总体格莱姆矩阵，即对于所有 (i, j) ∈ [n] × [n]，我们有：

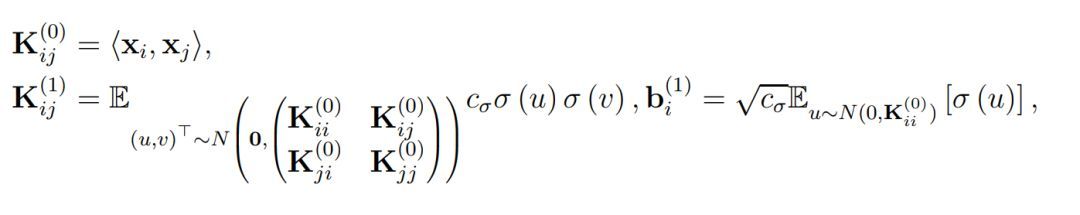
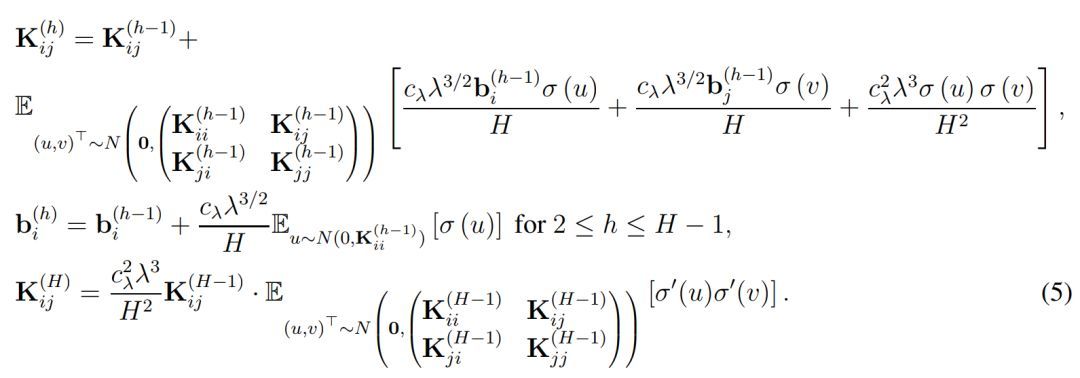
直观上而言，K^(h) 表示了在经过复合 h 次 核函数 后所得到的格莱姆矩阵（Gram matrix），其中 核函数 都是由 激活函数 σ所定义。此外，当 权重 矩阵的长和宽 m 趋向于无穷大时，它们会渐进格莱姆矩阵。因此作者做了以下假设以决定 收敛 率和过 参数 化总量：

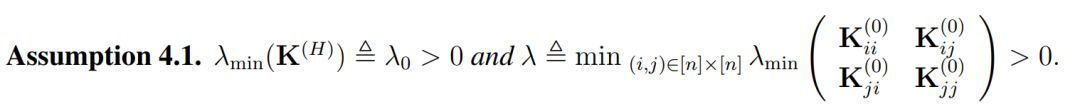
注意 λ 在这里仅依赖于 K^(0)，因此它的定义与全连接网络中的不太一样。一般而言，除非两个数据点是平行的，否则λ通常都是正数。在有了这个假设以后，作者给出了他们对 ResNet 的主要定理：