(点击上方蓝字，快速关注我们)
编译：伯乐在线专栏作者 - Ree Ray
如有好文章投稿，请点击 → 这里了解详情
我们将对同一群体内两种文化特征（cultural traits）的相互竞争进行建模。这是典型的文化动力学（cultural dynamics）场景：个体必须在两个或多个的互斥（mutually exclusive）项（诸如宗教信仰，选举，足球比赛）中选择一个。在本例中，我们对个体必须抉择（例如你不能信仰两个宗教）的情况十分感兴趣，当然，更复杂的情况：个体可以有多个选择，也不难实现。
随着时间的推移，个体会改变原有的选择。最终的决定取决于每种文化特征的输出（payoff）。输出是对特征相关影响（relative interest）的衡量，根据：
a）有多少人呈现出这种特征，以及
b）特征的吸引力（attractiveness）。
类似这种动力学的例子可以是两个不同宗教间的竞争。某些信仰因为有人信仰而变得更有吸引力。但是另一些信仰本质上对群体中的部分个体更有吸引力，即使他们只是小众。最后，因为社会准则不是静止不变的，所以特定信仰的吸引力也会随时间发生改变。
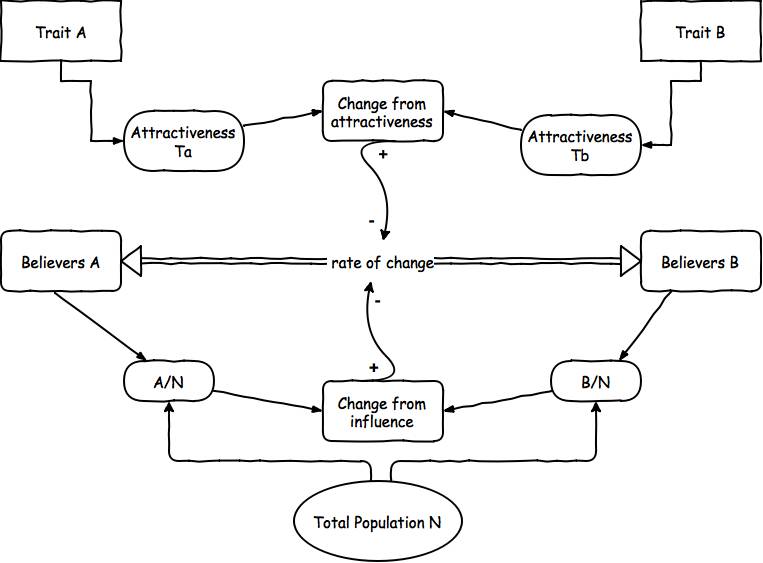
假定时间是离散的，从 t = 0 开始。
在每个时刻 t，两个群体 At 和 Bt 按照个体从 A 到 B 以及 B 到 A 的流动进行更新。这里值可以为负数，那就代表从 B 流动到 A 的人更多。
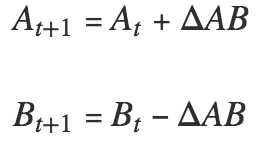
让我们想想这些怎么用代码实现。
首先，我们需要定义群体中个体的数量。假定开始有 100 人。“井”号后面的文字是你可以忽略的注释，不过这通常是为代码留下说明的好办法。
N = 100 # 群体人数
接着，我们需要决定每种文化（假定是宗教信仰）一开始有多少的信众（believers）。
A = 65 # A 类信众的初始数量
B = N - A # B 类信众的初始数量
最后，我们想在每个时刻根据差值（variation）来更新这些量：
t = 0
MAX_TIME = 100
while t < MAX_TIME:
A = A + variation
B = B - variation
# 进入到下一个迭代
t = t + 1
输入这些代码。记得留意缩进，这很重要。
按下 F5（或者点击绿色的三角）运行代码。会发生什么？
好吧，没什么发现，反而报错了。
NameError: name variation is not defined
事实上，我们还没有定义“variation”。让我们通过群体特征转换的数量和输出的差值来计算它。例如，如果 B 的输出更高，那么 A 就会像这样：
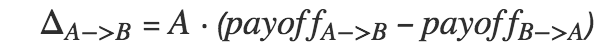
所以群体 A 流动到 B 的差值（proportion）与输出的差是成正比的（proportional）。正如我们前面所提到，文化特征的输出是由群体呈现的竞争特征和其自身的吸引力共同决定的。
为了定义输出，我们需要实现以下的竞争关系式：
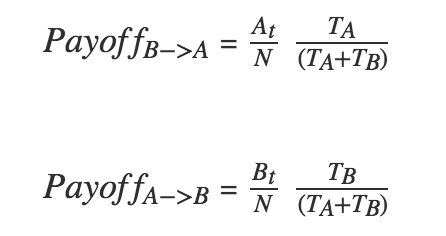
我们认真观察一下这个等式。第一项是整个群体 N 包含特定文化特征的比例（AA 占比为 At/N， BB 占比为 Bt/N）。而等式中的第二项是给定文化特征吸引力（TA 和 TB）对于总的“已有（available）”吸引力（TA + TB）的比值。
你也许很快就注意到这两个等式结构相同，唯一不同的是输入项。因此，为了避免不必要的麻烦（hassle），我们会创建一个“通用（universal）”函数。将以下代码放在脚本的开头：
def payoff(believers, Tx,Ty):
proportionBelievers = believers/N
attraction = Tx/(Ty + Tx)
return proportionBelievers * attraction
让我们稍微分析一下。首先我们定义函数并给定输入——信众的数量以及每种文化的吸引力。
def payoff(believers, Tx, Ty):
接着我们计算这两个值：
1.群体中信众的比例
proportionBelievers = believers/N
2.当前文化的吸引力
attraction = Tx/(Ty + Tx)
观察以上的等式，第一项是 At/N 和 Bt/N 部分，第二项是 TA/(TA+TB)。最终我们将得到计算结果。
return proportionBelievers * attraction
瞧！我们已经用 Python 代码实现了这个等式。现在，让我们修改主函数的循环来调用函数——我们需要调用两次来获取 A 、B 间相互流动的输出。每次循环迭代的时候都会重复，所以每次都会传入不同的值。为了得到 A、B 间互相流动的输出，我们在循环的开头也调用了“payoff”函数。
while t < MAX_TIME:
variationBA = payoff(A, Ta, Tb)
variationAB = payoff(B, Tb, Ta)
A = A + variation
B = B - variation
# 进入到下一个迭代
t = t + 1
这样，我们就传入了信众数量和文化吸引力的值。传入的顺序至关重要。B 流向 A 时，“believers’”的值等于 B，“Tx”的值等于 Ta，“Ty”的值等于 Tb。第二行表示的是 A 流向 B 的转化，“believers’”的值等于 A，“Tx”的值等于 Tb，“Ty”的值等于 Ta。
这次赋值过后没有定义每个文化特征的“attractiveness”值是个硬伤。因此需要在脚本的开头，即其它定义（N，A，B，MAX_TIME 等）附近加入定义。
Ta = 1.0 # 文化特征 A 初始吸引力
Tb = 2.0 # 文化特征 B 初始吸引力
alpha = 0.1 # 流动过程的强度
现在我们可以计算每次的输出差值了。这么一来我们应该观察哪种文化更有吸引力（A 还是 B）。
difference = variationBA - variationAB
如果差值是负数，我们知道此时 B 要比 A 有吸引力。反之，如果是正数，则 A 比 B 更有吸引力。接下来为了观察在这样的输出差值下有多少个体流动，我们可以在主程序的 While 循环中加入：
# B -> A
if difference > 0:
variation = difference*B
# A -> B
else:
variation = difference*A
# 更新群体
A = A + variation
B = B - variation
我们引入一个新的参数——α（alpha），用来控制 A、B 间流动的强度。在我们调节群体 A 和 B 前，这个参数会反复变化。
variation = alpha*variation
我们需要将它加入到模型剩下的参数中：
# 时间维度
MAX_TIME = 100
t = 0 # 初始时刻
# 初始种群
N = 100 # 群体数量
A = 65 # 群体中信众 A 的初始值
B = N-A # 群体中信众 B 的初始值
# 附加参数
Ta = 1.0 # 文化特征 A 初始吸引力
Tb = 2.0 # 文化特征 A 初始吸引力
alpha = 0.1 # 流动过程的强度
你应该注意到了主循环代码应该在流动（transmission）函数和初始变量的后面（因为它们在这需要用到）。编辑完成后应该是这样的：
while t < MAX_TIME:
# 计算当前时刻信众 A 与 B 改变后的输出差异
variationBA = payoff(A, Ta, Tb)
variationAB = payoff(B, Tb, Ta)
difference = variationBA - variationAB
# B -> A
if difference > 0:
variation = difference*B
# A -> B
else:
variation = difference*A
# 利用 α 参数控制改变速度
variation = alpha*variation
# 更新群体
A = A + variation
B = B - variation
# 进入到下一个迭代
t = t + 1
好，我们已经把所有需要的都准备妥了，如果运行代码，计算机在后台会重新计算所有的值。然而，因为没有输出，所以我们根本不知道发生了什么。让我们利用可视化来观察信众间的流动。首先，我们应该创建两个空的列表。其次，我们应该将初始群体添加到列表中。接下来，我们应该把每个时刻信众的数量添加到对应列表中。最后，我们该在仿真的结尾通过绘图来观察它们如何变化。先创建两个空列表。把下列代码块加入到代码开头，也就是变量定义和 while 循环中间：
# 初始化列表用以绘图
believersA = []
believersB = []
# 添加初始群体
believersA.append(A)
believersB.append(B)
代码开头的初始化/定义代码块应该像下面这样：
# 初始化
MAX_TIME = 100
t = 0 # 初始时刻
N = 100 # 群体数量
A = 65 # 种群中信众 A 的初始值
B = N-A # 种群中信众 B 的初始值
Ta = 1.0 # 文化特征 A 的初始吸引力
Tb = 2.0 # 文化特征 B 的初始吸引力
alpha = 0.1 # 流动过程的强度
# 初始化列表用以绘图
believersA = []
believersB = []
# 添加初始群体
believersA.append(A)
believersB.append(B)
我们只添加了信众的初始数量到对应的列表。然而，我们也需要在每个时刻结束时这样做。在 While 循环最后加入如下代码——记住和前面一行的缩进对齐！
believersA.append(A)
believersB.append(B)
整个 While 循环代码块应该像下面这样：
while t < MAX_TIME:
# 计算当前时刻信众 A 与 B 改变后的输出差异
variationBA = payoff(A, Ta, Tb)
variationAB = payoff(B, Tb, Ta)
difference = variationBA - variationAB
# B -> A
if difference > 0:
variation = difference*B
# A -> B
else:
variation = difference*A
# 利用 α 参数控制改变速度
variation = alpha*variation
# 更新群体
A = A + variation
B = B - variation
# 将值存入列表中用以绘图
believersA.append(A)
believersB.append(B)
# 进入到下一个迭代
t = t + 1
最后，让我们把结果绘制出来。第一步，我们要导入 Python 的绘图库，Matplotlib 并预定义绘图风格。把下面两行代码加入你的脚本的开头：
import matplotlib.pyplot as plt # 导入绘图库
plt.style.use('ggplot') # 让图片看起来更美观
下面，开始绘制吧！在 Python 中绘图就像说“帮我绘制这些数据”那么简单。在代码结尾加入这两行代码。我们只想在仿真结束时绘制一次结果，所以确认这两行代码不在 While 循环中——还应该保证没有缩进。运行代码！
# 绘制结果
plt.plot(believersA)
plt.plot(believersB)
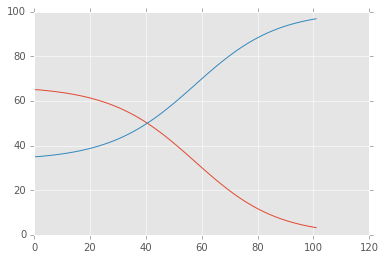
你可以看到随着时间变化两类信众的增减。吸引力 Tb 高于 Ta 并不十分意外。然而，你是否能想象出怎样的参数配置不会对群体产生影响？试着设置不一样的初始值来观察什么样的组合能打破（counteract）这种模式。
把 A 的初始值分别设置为 5，10，25，50，75，
把 MAX_TIME 设置为 1000，
把 Ta 和 Tb 设置为 1.0，10.0，0.1，0.01 等等，
把 α 分别设置为 0.01 和 1.0
你可以尝试所有可能的参数配置来观察群体间的流动有多快，也可以看看每个变量妨碍流动的最小值是多少。
然而，如果我们让每次流动时的吸引力随时间改变，那这个模型就更有趣了。让我们定义一些函数来实现这个想法。把下面的函数添加到 While 循环的开始处（记得缩进！）。
Ta, Tb = attractiveness(Ta, Tb)
Ta 和 Tb 将按照我们所期望的模型动力进行改变。让我们定义“attractiveness”函数。我们已经在写过“payoff”函数了，所以这应该只是小菜一碟。在每个时刻，我们都会用我们定义的内核（kernel） K 来细微改每个文化特性的吸引力。如下表达：
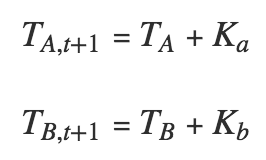
K 的几种情况如下：
让我们在一些简单的场景中开始，例如 a）Ta 在每一时刻都将随固定的 Ka 增加， b）Kb 等于 0（所以 Tb 在整个模拟中都是固定的）。
def attractiveness(Ta, Tb):
Ka = 0.1
Kb = 0
Ta = Ta + Ka
Tb = Tb + Kb
return Ta, Tb
首先，我们定义函数并给出输入：
def attractiveness(Ta, Tb):
接着，我们确定每个文化特性的吸引力改变了多少（也就是定义 Ka 和 Kb）
Ka = 0.1
Kb = 0
加入等式中：
Ta = Ta + Ka
Tb = Tb + Kb
最后，返回新的值：
return Ta, Tb
这就是该函数的功能。主循环现在像下面这样：
while t < MAX_TIME:
# 更新吸引力
Ta, Tb = attractiveness(Ta, Tb)
# 计算当前时刻信众 A 与 B 改变后的输出差异
variationBA = payoff(A, Ta, Tb)
variationAB = payoff(B, Tb, Ta)
difference = variationBA - variationAB
# B -> A
if difference > 0:
variation = difference*B
# A -> B
else:
variation = difference*A
# 利用 α 参数控制改变速度
variation = alpha*variation
# 更新群体
A = A + variation
B = B - variation
# 将值存入列表中用以绘图
believersA.append(A)
believersB.append(B)
# 进入到下一个迭代
t = t + 1
如果进行绘图，你会得到和之前不一样的结果：
plt.plot(believersA)
plt.plot(believersB)
试着改变 Ka 和 Kb 的值，看看会发生什么。你能发现使两个文化特性共存（coexist）的均衡（equilibrium）吗？
这有些函数可以用来动态改变每个文化特性的“吸引力”，试着用一下：
import numpy as np # 这行紧跟在脚本开始处其它的“import”
def attractiveness2(Ta, Tb):
# 随机时序自相关（temporal autocorrelation with stochasticity）（正态分布）
# 我们将得到正态分布 N(0,1)的两个采样
Ka, Kb = np.random.normal(0, 1, 2)
# 计算 Ks 的差
diff = Ka-Kb
# 将 Ks 的差与吸引力进行运算
Ta += diff
Tb -= diff
return Ta, Tb
def attractiveness3(Ta, Tb):
# 反盲从（anti-conformism）动力学（群体越多吸引力反而越小）
# 初始化都为 0
Ka = 0
Kb = 0
# 首先我们用 mean=last popSize（相关时刻下的群体 A）对 gamma 进行采样
diffPop = np.random.gamma(believersA[t])
# 我们用这个值减去经过相同计算的群体 B
diffPop = diffPop - np.random.gamma(believersB[t])
# 如果 B 更大，我们需要提高 A 的吸引力
if diffPop < 0:
Ka = -diffPop
# 否则如果 A 更大，我们需要提高 B 的吸引力
else:
Kb = diffPop
# 改变当前值
Ta = Ta + Ka
Tb = Tb + Kb
return Ta, Tb
利用上述函数（只修改“attractiveness”函数，例如改为“attractiveness2”），加入些微的动态变化时，观察将会发生什么改变。如果初始条件改变，会发生什么变化？如果迭代时间更长又会怎样呢？
看完本文有收获？请转发分享给更多人
关注「Python开发者」，提升Python技能
