初听到0.99999…=1都会吓一跳,不符“常识”,解释之后又感觉数学的魅力所在。
还有那些这样的例子?
再比如:
给地球和小皮球做一个紧箍的钢环,同时给钢环扩大1米,哪个球的平均空隙大?(答案是一样大)
又如皮筋与蚂蚁问题:
一只蚂蚁在理性弹性绳的一端,向另一端以每秒1cm的速度爬行。弹性绳同时以每秒1m的速度均匀地拉长,蚂蚁能否爬到终点?
看起来不行吧?没错,答案是“能”。
简单的解释就是假设弹性绳的速度是每秒0.9cm,那么直觉上蚂蚁就能爬到终点。而弹性绳均匀拉长意味着其上总有一点的速度是每秒0.9cm,也就是说蚂蚁可以爬到这个点。接下来把整个弹性绳分段就好了。
另外没必要说高深的理论,一些简洁平凡的结论就挺有趣了。看起来难以理解,想一想就恍然大悟。
无穷是个很无赖的概念……什么构造出一个全体分数集(有理数)对应正整数集的……
级数里面全体自然数之和为-1/12
微积分当中最妙又最简洁的当属“摆线长度等于圆直径四倍”,这条与圆息息相关,怎么看怎么“无理”的一条线,长度不仅和π没有关系,还是个漂亮的整数倍!:
当时知道“半球体积等于等底等高的圆柱切去一个圆锥的体积”的直观解释的时候真的是拍案称奇。
不知道算不算几何学,但是莱洛三角形 是挺神奇的。平稳地搬运东西不一定要用圆木。

而且,不说复杂的,三角形的四心(重心、垂心、内心、外心)也很神奇啊,三种重要的线都汇聚到某个点上。
迷宫的万能解法也挺流氓的……不过这个算图论或者拓扑学了……说到图论,四色猜想也很经典,然而这个不是“想一想就恍然大悟”的部分了……
对了,拓扑学里还有个“同胚”的神奇概念,例如下面这两个就是拓扑等价的:
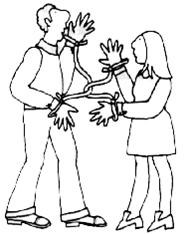
类似的,我们还可以得到“8字环和圆环同胚”的结论。在实际生活中也有应用:不打开绳结、不割断绳子,是可以把下图的两个人解开的。
代数算是比较按部就班的领域了……五次方程没有公式解是个挺令人沮丧的事实……
另外尺规作图无法三等分角也是挺令人沮丧的,更有趣的是这个几何问题要用比较深的代数方法解决。
不过有很多经典的问题可以归入代数:
上下山问题:上山速度3m/s,下山速度5m/s,平均速度不是4m/s。
芝诺悖论:
阿基里斯的速度是乌龟的百倍,乌龟在阿基里斯前一百米。当阿基里斯跑到乌龟现在的位置时,乌龟多跑出去了一米;阿基里斯追上这一米时,乌龟又多跑了一厘米;以此类推,阿基里斯永远追不上乌龟。(0.999…=1与芝诺悖论是异曲同工)
数论里有个很妙的结论,N之前素数的分布频率与ln(N)/N几乎相合,更准确的版本是:
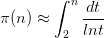
对了,调和级数是发散的!
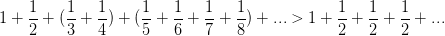
另外……既然提到了0.999...我觉得有很多日经问题都可以说呀:
三门问题:
三扇门背后只有一扇门有奖金,另外两扇是空门。参与者选择一扇门后,主持人打开余下两扇门中一扇空门。这时参与者换门获奖率是2/3,不换门的获奖率是1/3。
(说实话我到现在还是不明白为什么有人会觉得两扇门获奖率一样……)
男女孩问题:
一家人有两个孩子,其中有一个女孩。另一个孩子是男孩的概率是2/3。
“魔术师地毯”类问题:
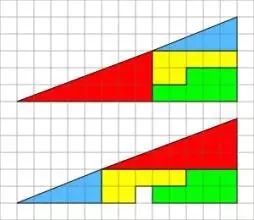
生日悖论:
23人中有两人生日相同的概率大于50%,50人时就可以升高到97%。
下面这个来自M67的Blog,告诉你为什么大家不把“找规律填数”当数学:
圆上有 n 个点,两两之间连线后,最多可以把整个圆分成多少块?上图显示的就是 n 分别为 2 、 3 、 4 的情况。可以看到,圆分别被划分成了 2 块、 4 块、 8 块。规律似乎非常明显:圆周上每多一个点,划分出来的区域数就会翻一倍。
事实上真的是这样吗?让我们看看当 n = 5 时的情况:
果然不出所料,整个圆被分成了 16 块,区域数依旧满足 2n-1 的规律。此时,大家都会觉得证据已经充分,不必继续往下验证了吧。偏偏就在 n = 6 时,意外出现了:
此时区域数只有 31 个。
下次还有人问你找规律填数,没啥兴趣的话可以这么回答:答案是oo,因为这是一个以xx为周期的循环数列。














