基础准备
前段时间我们介绍的都是逻辑回归方面的内容,根据分类型因变量的类别数不同,逻辑回归模型可以分为二元逻辑回归模型、有序多元逻辑回归模型和无序多元逻辑回归模型:
逻辑回归模型只是分析分类型因变量的其中一种最常用的分析方法。今天我们要介绍另一种分类型因变量的回归模型:Probit回归模型。
Probit回归模型与Logistic回归模型的功能类似,根据因变量的不同,可以分为二分类、有序多分类和无序多分类三种情况。因为Probit回归模型与Logistic回归模型的功能类似且分析结果不易解读,所以Probit回归模型的应用不如逻辑回归模型广泛。下面将以二分类因变量为例介绍Probit回归模型。
Probit回归模型
Probit回归模型的“Probit”是英文单词Probability的意思,它的回归模型可以用下面的式子来表示:

由回归模型的公式可知,Probit回归模型是建立在正态分布的理论基础之上的,对比逻辑回归模型,Logistic回归模型是建立在二项分布的基础之上。虽然两种回归模型的原理和分析结论类似,但是根据它们的模型原理,连续性的自变量较多且服从正态分布时,可以考虑Probit回归模型;分类型的自变量较多时,就使用Logisitc回归模型。
Probit回归模型的回归系数(ai)含义与其它回归模型的类似,表示其它自变量取值保持不变时,该回归系数对应的自变量每改变一个单位,出现阳性结果的概率密度函数值的改变量。下面我们来介绍如何用SPSS软件做Probit回归分析。
案例分析
古人云:“是药三分毒”,药物本身就是有毒物质,它既可以治病,但是超过一定的摄入量,也会对肌体造成伤害甚至引发死亡。《黄帝内经》中写道:大毒治病,十去其六,常毒治病,十去其七,小毒治病,十去其八,无毒治病,十去其九;谷肉果菜,食养尽之,无使过之,伤其正也。例如很多电视剧里演绎的自杀情节,主人公服用大量的安眠药自杀,少量的安眠药有助睡眠,大量的安眠药就让人一觉不醒。
大家如果注意观察,会发现在很多的药物说明书上都会标注一项药物毒理学指标:半数致死剂量(简称LD50),它表示动物一次摄入有毒物质后,在一定时间和条件下,半数死亡所使用的有毒物质剂量,这项指标常用来表示药物的毒理特性。例如,生活中常用的消炎药阿司匹林的LD50大概为1500mg/kg(不同厂家的产品略有不同)。计算LD50的方法多达20多种,下面我们介绍如何用Probit回归模型来计算药物的LD50。
前几年经常有喝散装白酒或假白酒致死的新闻,这是因为这些酒中的甲醇含量超标造成的。下面介绍如何测定甲醇的半致死剂量及其95%置信限。实验设计方案:选取60只实验小白鼠,体重在19~21g之间,随机分成6组,每组10只雌雄各半,按照甲醇的实验剂量分别命名为12000、9600、7680、6144、4915.2和3932.16mg/kg组。配置6种甲醇的实验液,分别为600、480、384、307.2、245.8、196.6mg/mL。每组小鼠按照0.2ml/10g的剂量灌胃给予上述实验液,给药后即刻观察动物反应情况并继续观察72小时,记录各组小白鼠的死亡情况,实验结果如下:
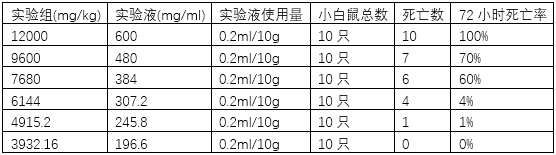
数据输入到SPSS中,是以下形式:
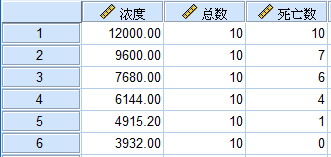
(例题数据文件已经上传到QQ群,群号请见文章底部温馨提示)
分析步骤
1、选择菜单【分析】-【回归】-【概率】,在跳出的对话框中,将死亡小白鼠数量选为响应频率,将每组小鼠选为实测值总数;将每个实验组的实验液浓度选为协变量;然后选择以10位底的对数作为协变量的转换方式。
这主要是从药理、毒理等学科的专业出发,选择对自变量进行对数或自然对数变换。通常进行对数变换后的剂量与死亡率之间呈对称的S型曲线,而未进行对数变换的剂量与死亡率之间为长尾S型曲线。因此这里选择以10为底的自然对数。
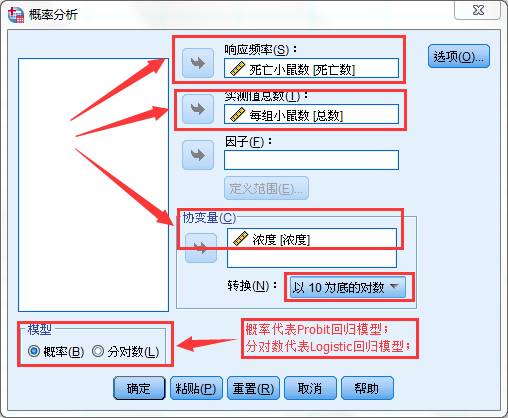
2、点击确定,输出结果。
结果解释
1、参数估算值表;从表格中的显著性可以知道,不同浓度的甲醇溶液对小白鼠的致死率的确存在不同的影响。
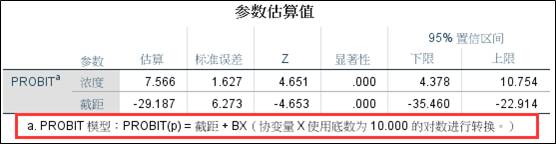
表格中输出了Probit回归模型的参数估计值机器显著性。在表格的底部,同时注明了本案例的Probit回归模型公式。
2、模型的拟合优度检验;从检验结果来看,模型的卡方检验显著性达到0.672,远大于0.05,所以模型的拟合效果是非常好的。下方的表格显示了实测响应与模型计算得到的期望响应的结果,同样可以看出两者的差距非常小。
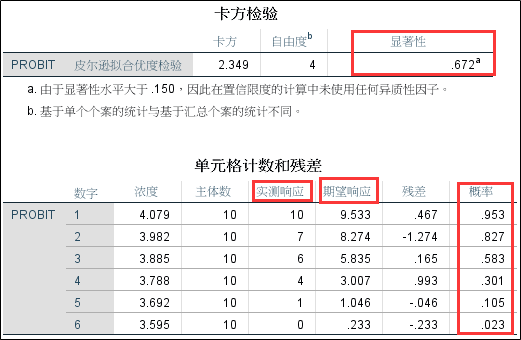
3、概率估计值表;从表格可知,当死亡率为50%时,对应的甲醇剂量为7202.773mg/kg。
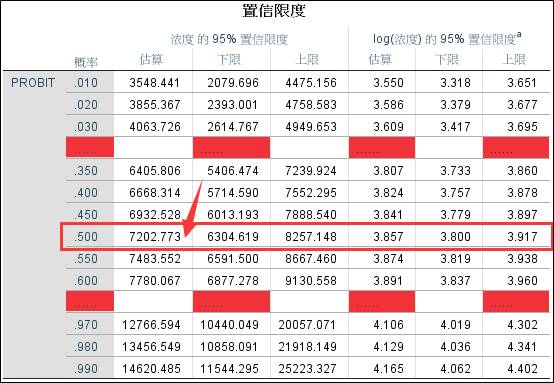
从以上实验的分析结果可以知道,生活中不能胡乱服药,也不能过量服药,一定要遵照医生及药品说明书使用药物。大毒治病,十去其六,常毒治病,十去其七,小毒治病,十去其八,无毒治病,十去其九。
生活统计学,这里不仅有各种数据分析方法,更有容易被大家忽视的生活常识。
所有例题的数据文件都会上传到QQ群中,需要对照练习的朋友可以前往下载,QQ群号见下方温馨提示。
温馨提示:






