利率精算法（1）

写这篇文章之前，是因为我遇到一个麻烦。徘徊犹豫在二个抉择之间；1）我可以用父母名义贷款，第一套房，利率6.655%，贷8年；2）我可以用本人名义贷款，第二套房，利率8.613%，贷30年。

很多人可能会问，这有什么好选的。当然是选1），利率差太多了。

这个说法并不对。事实上，真正的精算结果。应该是方案2）更优惠一点。

利率最低的贷款，并不一定是最佳的贷款。

真正的好贷款，有二项因素，一是利率，二是还款速度。

为了展开一下，让我们先看一下下表，假设1000000元贷款。

当100万元贷款，6.655%利率贷8年，每个月还款额13462元。累计支出129万元。当100万元贷款，8.613%利率贷30年，每个月还款额7769元。累计支出279万元。

乍一看，似乎方案2远远不利。因为他累计支出足足要279万元。几乎是方案一的翻倍。这也是6.655%优惠利率的直观感觉。很多人想也不想，就选择了方案一。

但实际情况，并不是这样。奥妙，就藏在第三栏的+5693元中。

我们观察一下第三栏，歧视利率贷款30年，虽然总支付较多。但一开始，每个月还款却很少，仅七千余元。
在最初的“八年”之中，选择方案2的人，每月都可以多+5693元的现金流。然后在余下的22年中，每月支出-7769元。

5693*8年 – 7769*22年，这笔帐打不打得平呢。仔细计算一下，其实还是可以打平的。这就是复利的奥妙。

假设我每月可以获得0.8%的回报，也就是每年10%左右。则“定期定供”的结果，到第96年个月的结尾，这笔钱已经滚存成近81万元的巨款。

在此后的22年之中，每月从帐户里抽取-7769元。帐户虽然缩小，但因为有复利的支撑，这笔钱缩减很慢，一直到第328个月，才刚刚为零。到第360个月，也不过多付二三年月供罢了。

如果我们再进取一点，假设我们回报能做到12%，代入公式算一算。结果不得了。居然是正数！大概到期末，还能剩下200多万的巨款。

所以说，“8.613%贷30年”未必不好，只要我们把现金持有手中，获取10~12%回报。卅年以后，回报甚至比“6.655贷8年”更佳。

这其中盈亏平衡点是多少呢？这个问题不太好算，需要用Excel展开，不过结果已经算好了。大致是10.42%。

利率精算法（2）

在此处，我们再探讨一下公积金的问题。公积金的利率非常低，五年期以上只有5.22%。而商业贷款是6.655%。

公积金的劣势，是他的贷款年限非常短，只有15年。

这在利率精算法的仔细分析下，某些情况下，长周期商贷，仍然能跑赢公积金。只不过回报要求比较高。

同样算法，假设1000000元贷款，15年公积金和30年普通商业贷款：

把这±现金流，代入复利的计算器，最终结果大约在9.71%。
也就是说，只要我能保证自己投资，能达到9.71%的回报率。即使是如此诱人的公积金，还是商贷划算。

如果我们换个想法，10年公积金呢。“30年商贷vs10年公积金”，这也可以算，结果大约是8.12%
如果12年呢，大约是8.60%
如果11年呢，大约是8.34%
。。。。。。

这个问题，还可以一直问下去。包括8年，7年，6年。。。。。。
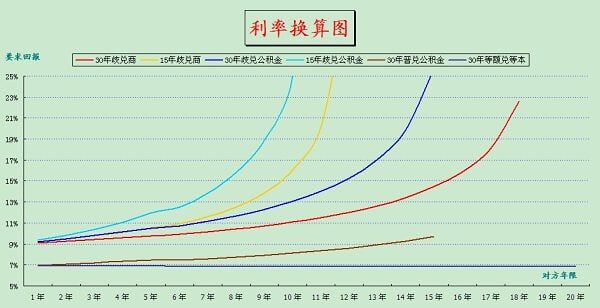
为了便于读者计算，我们画了下图《利率换算图》

下图表示了，当我是30年第二套房利率，我父母是8~12年普通商业贷款，我需要达到多少回报率，才可以持本。

分别画了六根线：

• 我是30年第二套房，父母普通商业贷款（1~30年）

• 我是15年第二套房，父母普通商业贷款（1~30年）

• 我是30年第二套房，父母可贷公积金贷款（1~15年）

• 我是15年第二套房，父母可贷公积金贷款（1~15年）

• 我是30年第一套房，父母可贷公积金贷款（1~15年）

• 我是30年第一套房，父母却选了等额本息（1~30年）

利率精算法 （3）

闲来无事，我们又算了第二张图《盈利换算图》。

还是回到我们最原始的问题，我有二个选择；1）以父母的名义贷款，利率6.655%，贷8年。2）以我的名义贷，利率8.613%，贷30年。我们已知这种做法的盈亏平衡点，是自有资金回报10.42%。

但如果我心中惴惴，假设我能力不到，只能够做到9%。那我会亏多少钱，会不会造成大灾难？

在本贴的后面，我们留了一个Excel，其中第二行，就是“利率求返点”。

把9.00%输进去，得出的答案是-66244。也就是说，不恰当地贷款拖长，使我相当于买了一套106.6万元的房子。

嗯，这虽然不令人愉快，但仍然是可以承受的。不算得是灾难。Go!

在《盈利换算图》中，我们设计了九种贷款方案。

以“30年等额本息”为基准，画了其他八种方案，与他的比例。曲线越低越好，相当于房款打折。

当各位预估了自己的收益后，可以选择最优的贷款方案。
当各位估错了自己的收益后，可以知道自己损失的金额。

这九种贷款方案分别为：

1）20年第二套房（红）
2）10年第二套房（黄）
3）20年第一套房（靛）
4）10年第一套房（蓝）
5）15年公积金  （黑）
6）10年公积金  （褐）
7）30年等额本金（绿）
8）15年等额本金（青）
9）30年第一套房，此线与X轴重合，恒为0

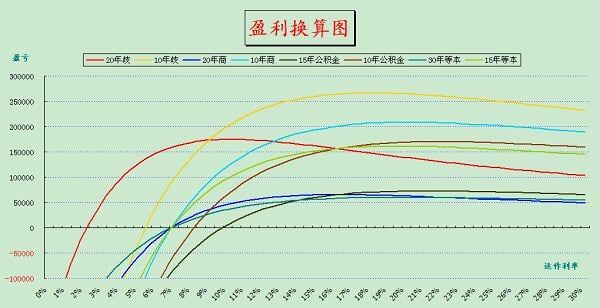
（注：值得注意的是，当利率超过9.71%，方案9“三十年等额本息”，就跑赢了其他所有选择。恒胜利）

（[email protected]，2007年11月9日晚）