终端之间信息传递安全性的保证始终是业务的刚性需求。不同的加密算法针对不同的业务需求,
因为公司是金融公司性质,又不是传统的金融公司(PS:牵扯到数字货币、常听说的比如:
比特币
),加密算法这块也算是有一部分的了解。
这里要讲的内容如
标题
😄
数字签名
-
数字签名就是类似纸质文件上的手写签名的电子版。任何人都可以轻松地核对签名,不能伪造它是其存在的根本目的。
-
数字签名可以为签名者身份和其签署的信息内容提供证明。
-
对于电子签署的商业性合同,电子支票,电子购货单和其他一些各方希望进行认证的电子信息来说是一种理想的解决方案。
素数
在密码学中需要找到最大的随机素数是必须的。大素数很多,通常测试适当的随机整数,知道找到素数的过程是可行的。
素数的分布函数 π(n): 描述了小于或等于n的素数的数目
素数定理给了 π(n) 一个有用近似:
$$ \lim_{n \to +\infty} \frac{π(n)}{n/(\ln n)} \quad = 1 $$
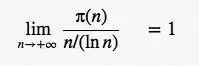
e.g:
当 n = 10^9 时其误差不超过 6% 其:π(n)=508,475,34,且 n/ln * n≈ 482,549,42
伯努利实验
RSA基于素数原理:寻求大素数是很容易的,把一个数分解成两个最大素数的积却相当的困难
公钥加密
公钥加密,顾名思义有一把
公钥
与
私钥
在 RSA 加密算法中,每一个秘钥由一对整数组成。在密码学中常以
Alice
与
Bob
作为例子,这也是每当有人普及比特币相关的技术的时候频率出现较多的名词。
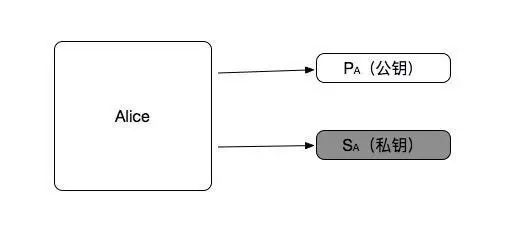
如图:用 $P_A$ 表示
Alice 公钥
,$S_A$ 表示
Alice 私钥
同理:
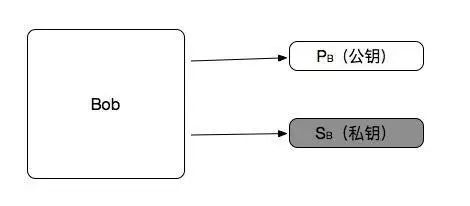
如图:用 $P_B$ 表示
Bob 公钥
,$S_B$ 表示
Bob 私钥
秘钥需要保密,公钥可以对任何人透露,这个跟比特币地址是一样的。
公钥和秘钥指定了可用于任何信息的函数。设 $\mathfrak{D}$ 表示允许的信息集合。其可能是所以有限长度的位序列的集合。
在最原始的公钥加密设想中,要求公钥与秘钥指定一种从
$\mathfrak{D}$ 到其自身的一一对应的函数。对应 Alice 的公钥 $P_A$ 的函数用 $P_A()$ 表示,他的秘钥
$S_A$ 的函数表示成 $S_A()$, 因此 $P_A()$ 与 $S_A()$ 函数都是 $\mathfrak{D}$
的排列。架设已知秘钥 $P_A$ 或 $S_A$,可以有效的计算出函数 $P_A()$ 和 $S_A()$
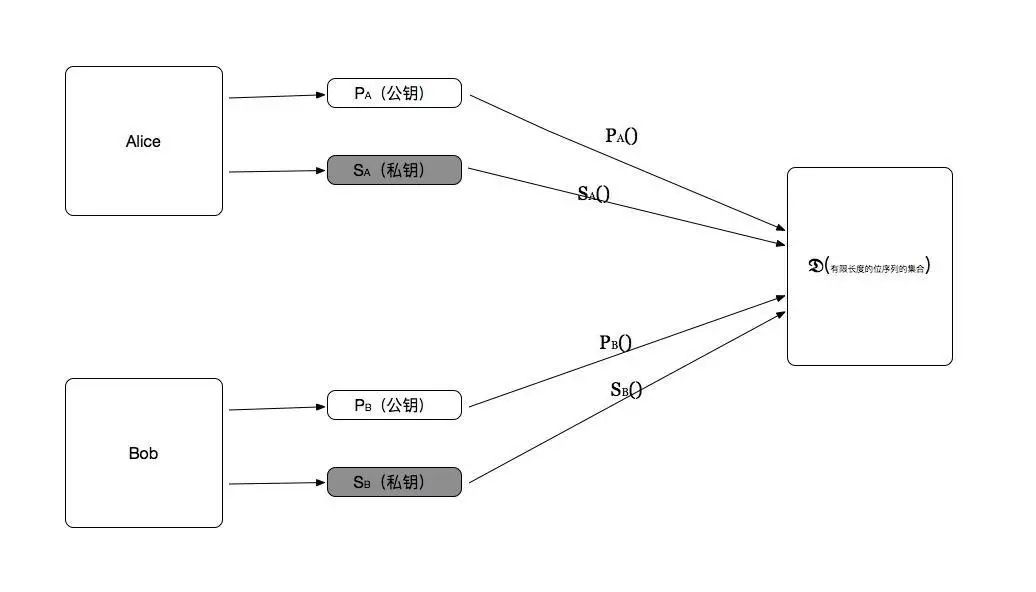
系统中任何参与者的公钥和秘钥都是一个“匹配对”,它们指定的函数互为反函数,也就是说,对于任何消息 $M\in\mathfrak{D} $ 有:
$$ M = S_A(P_A(M)) \ M = P_A(S_A(M)) $$
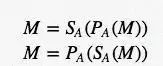
由此可以看出,运用两把秘钥 $P_A$ 和 $S_A$ 对 $M$ 相继进行变换后,最后任然得到消息 $M$
故在应用程序中:要求除了Alice外,没人能在较实用的时间内计算出函数 $S_A()$。 对于送给 Alice 加密邮件的保密性与 Alice 的数字签名的有效性。
因为$P_A$是公开的,就比如 数字货币的地址,这样就可以计算出 $P_A()$ 它也是 $S_A()$ 的反函数,这个时候就要保证只有 Alice 能够计算出 $S_A()$ 。
模拟一个发送环境:
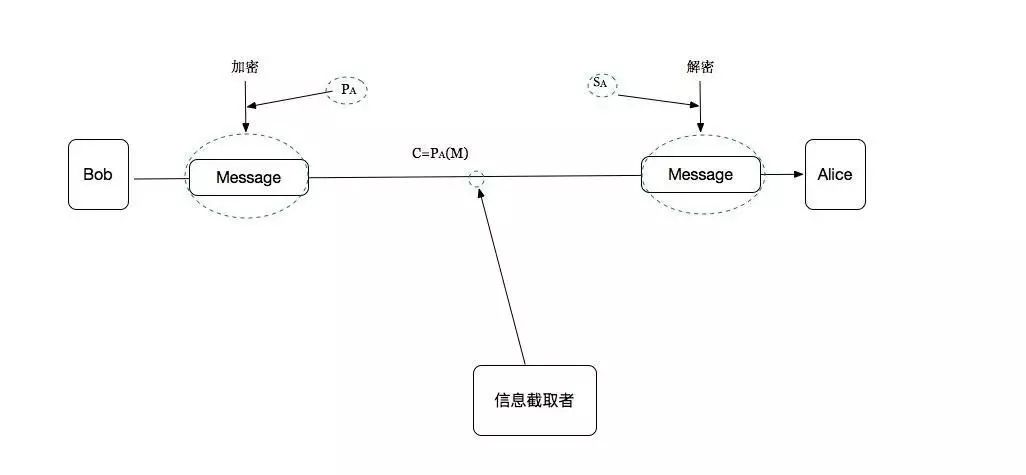
如上图:
Bob
给
Alice
发送一条加密的消息 Message,窃取着得到的是一串乱码。
-
Bob
得到
Alice
的公钥 $P_A$
-
Bob
计算出对应的
M
的密文 $C=P_A(M)$,并把 C发送给
Alice
-
当
Alice
得到密文C之后,运用自己的秘钥$S_A$恢复原始信息: $S_A(C)=S_A(P_A(M))=M$.
由于 $S_A()$ 和 $P_A()$ 互为反函数,所以
Alice
能够根据 C 计算出 M。因为只有
Alice
能够计算出 $S_A()$, 所以也只有
Alice
能根据 C计算出 M。因为
Bob
运用 $P_A$ 对M进行加密,所以只有 Alice 可以理解接收的消息。
用类似的公钥系统的设想可以很容易的实现数字签名,现在 Alice 希望把一个数字签署的答复 M^' 发送给 Bob
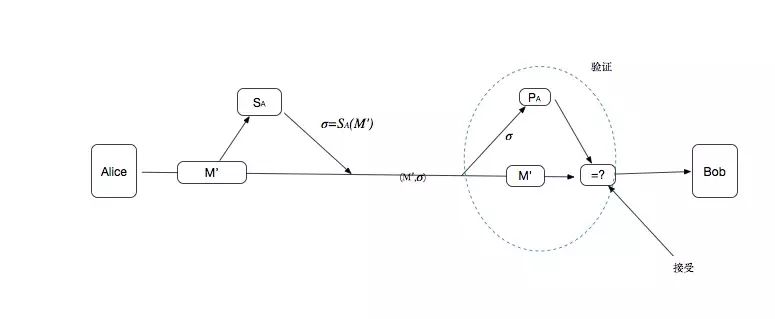
在公钥的数字签名中,
Alice 将她的数字签名 $\sigma = S_A(M')$ 附加到消息 M‘上,来对消息 M’ 签名。她将消息/签名对 $(M',
\sigma)$ 发送给 Bob,Bob 通过检查等式 $M’ = P_A(\sigma)$ 来验证它。如果等式成立,则他接受
$(M',\sigma)$ 作为 Alice 已
经签名的一个消息
-
Alice 运用她的秘钥 $S_A$ 和等式 $\sigma = S_A(M')$ 计算出信息 M’ 的数字签名 $\sigma$.
-
Alice 把消息/签名对 $(M', \sigma)$ 发送给 Bob.
-
当 Bob 收到 $(M', \sigma)$ 时,他可以利用 Alice 的公钥,通过验证等式 $M’ = P_A(\sigma)$ 来证实该消息的确是来自 Alice.
如果 M’ 包含 Alice 的名字,这样 Bob 就知道应该使用谁的公钥。
由上图中的验证可以看到,如果符合
Bob 可以得出消息 M‘ 确实是 Alice 签名的结论。如果不成立,那么 Bob 就可以得出一个结果: 要么就是信息 M‘或数字签名
$\sigma$ 因传输错误而损坏,要么信息对 $(M',\sigma)$ 是一个故意的伪造。
因为一个数字签名既证明了签署者身份,也证明了签署的信息内容,所以它是对文件末尾的手写签名的一种模拟
。
数字签名必须可以被能取得签署者公钥的人去验证,一条所签署过的信息可以被确认方确后再传送到其
他可以验证签名的各方。
比如我给你的一个比特币其实就是一个签名的过程,只是比特币采用的是多次签名加密技术,比这个要复杂许多(做区块链开发的人可能见笑了),其原理是怎样的呢?密码学中一个通俗的例子:
Alice 给 Bob 的一张电子支票,Bob 确认了支票上 Alice 的签名后,就可以把这张支票交送给银行,而银行也可以对签名进行一个验证,然后就可以调拨相应的资金。
上面讲到的是签署的信息是没有加密的,该信息是公开透明的,比如比特币交易的过程中是公开透明,该行为会向全网进行一个广播,同而使各个节点都能同步到该交易事件。
而我们这里要说的反而恰恰相反,我们要把信息进行一个加密,怎样去加密呢?就是把有关加密和签名的两种方案结合起来使用,就可以创建出同时被签署和加密的消息,签署者首先把其数字签名附加在消息的后面,然后再用他预定的接受者的公钥对最终的消息/签名对进行加密。接收者用其密钥对收到的消息进行解密,以同时获得
原始消息和数字签名。然后接收者可以用签署者的公钥对签名进行验证。很有意思!
RSA加密系统
公钥私钥创建过程
1.随机选出最大素数 $\mathcal{P}$ 和 $\mathcal{q}$, 使得 $\mathcal{P}\not=\mathcal{q}$ e.g:素数 $\mathcal{P}$ 和$\mathcal{q}$ 可能各有 1024 位。
2.计算 $n=\mathcal{P} \mathcal{q}$
3.选取一个与 $\phi(n)$互质的最小奇数 e,其中由等式 $\phi(n)$ 等于 ($\mathcal{P}-1$)($\mathcal{q}-1$)
4.对模 $\phi(n)$, 计算出 e 的乘法逆元 d 值。
5.将对 $P=(e,n)$ 公开,并作为参与者的
RSA 公钥
6.使对 $S=(d,n)$ 保密,并作为参与者的
RSA秘钥
设 $D$ 为集合 $Z_n$.为了变换与公钥 $P=(e,n)$ 相关的消息 $M$, 计算 $$P(M) = M^e\mod n$$
这个时候变换与秘钥 $S =(d,n)$ 相关的密文 C,计算 $$S(C)=C^d \mod n$$
上面所看到的等式对加密与签名是通用的。为了创建一个签名,签署人把其秘钥应用于待签署的消息,而不是密文中。为了确认签名,将签署人的公钥应用在签名中,而并非在加密的消息中。
用模的求幂过程,来对公钥与秘钥的一些操作。
我们设公钥(e,n)和秘钥(d,n)满足 $\lg e = O(1)$, $\lg d \leq \beta$, 且 $\lg n \leq \beta$.
然后,应用公钥需要执行 $O(1)$ 次模乘法运算和 $O(\beta^2)$ 次位操作。 应用秘钥需要执行 $O(\beta)$ 次模乘法运算 $O(\beta^3)$ 次位操作。
RSA安全性保证
RSA加密的安全性主要来源于对最大整数进行因式分解的困难性。如果对方对公钥中的模
n 进行分解,就可以根据公钥推导出秘钥,主要是因为对方和公钥创建者以同样的方法使用因子 $\mathcal{P}$ 和
$\mathcal{q}$ .故如果能够分解大整数,就可以轻易破解 RSA 加密算法。
这样来讲:对RSA加密系统的破解难易程度取决于分解最大整数的困难度。
在计算机发展的历史中至今还没有发行比分解模 n 更容易的方法来打破 RSA加密。





