武士如厕为何惊声惨叫
数学大师为何卧床不起
这一切的背后， 是人性的扭曲还是道德的沦丧？
↓ 看视频吧 ↓
——————————————
扩展猫粮
此时，你也许会大叫：“啊哟喂~视频最后出现的那些鬼畜至极的长的跟钱串子似的刀谱到底是什么鬼？？！！”
好了，先不说这些到底是什么鬼，先问你，前面的剧情全都看懂了吗？
嗯，你认真的想了想：“好像也并没有看
很
懂呀嘻嘻嘻。”
好的，那我们快速的回顾一下视频里提到的几套刀法。
凡夫俗子都能想到的方法
为了让挥刀面积最小，我们不妨先把武士刀换成线段，考虑让一条线段在平面上转过180°。多数人的第一反应是让线段绕着一端旋转 180° ，即半圈的情形。很显然，此时线段扫过的面积是π/2 。
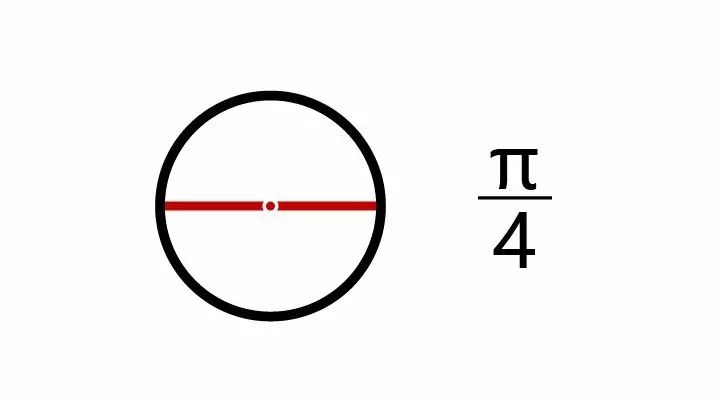
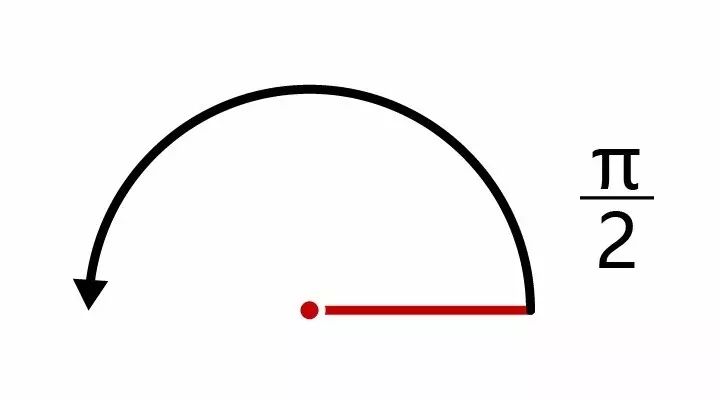当然，这是很差的一种设计。如果把旋转中心放到线段中点的位置，让线段绕中点旋转180°，情况就会好很多，这是线段扫过的面积为π/4。
挂谷宗一的见地
数学家们肯定不会考虑上述这些几乎没有技术含量的东西。在挂谷宗一提出这个问题后，有数学家发现，若这个线段在正三角形（高为 1，边长为 2/√3 ）中每一顶点处都旋转 60°，那么线段扫过面积为
√3
／3。
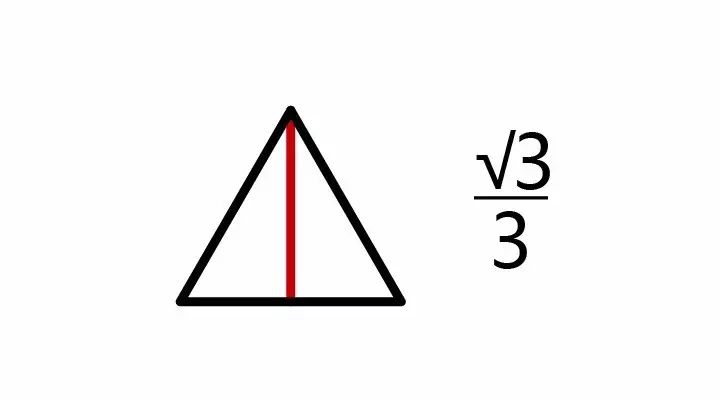挂谷宗一不满足于此，他想到了数学大师欧拉（Euler）发现的那个三尖瓣线（Deltoid curve）。
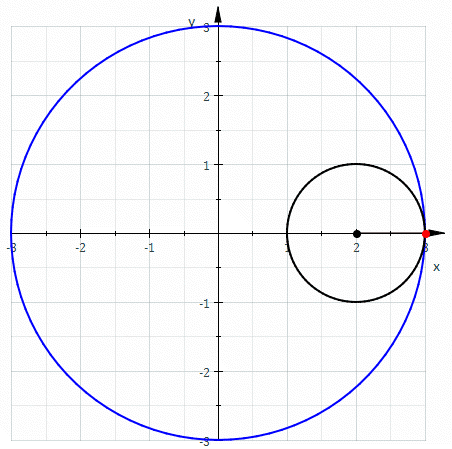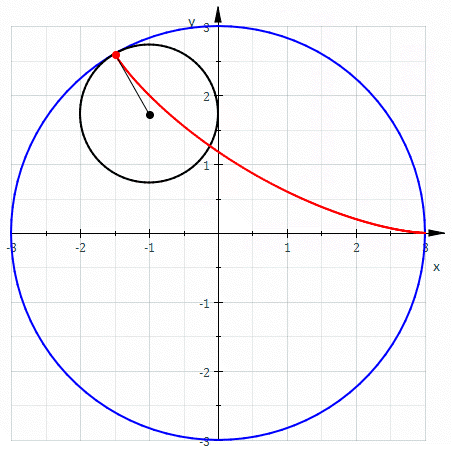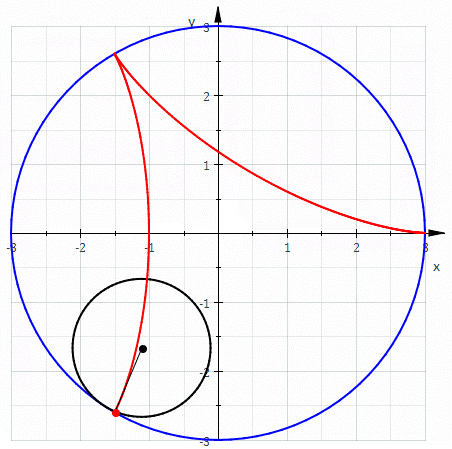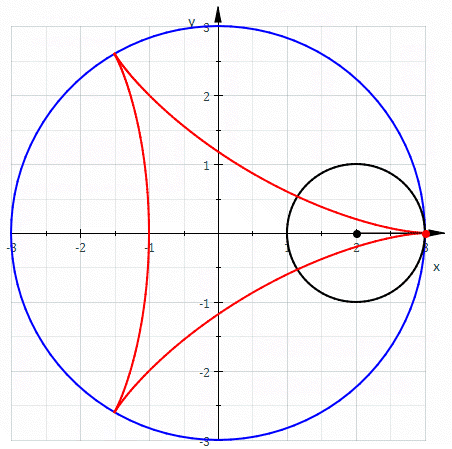
红色部分即为三尖瓣线
上图就是三尖瓣线的形成过程。当小圆直径为0.5，大圆直径为1.5时，三尖瓣线内部任何一条切线的长度均为1。
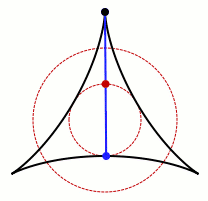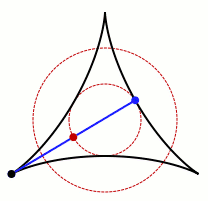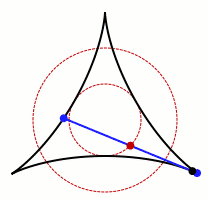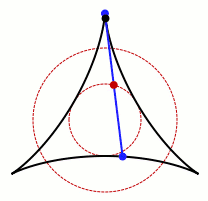
任意切线（蓝色）的长度均为1
这个三尖瓣线的面积刚好是“直径为1的圆的面积的一半（π/8）”。
挂谷宗一猜测，这就是最终答案——长度为1的线段旋转180°，扫过的最小面积为
π/8
。
我相信，就算有人给出了面积更小的答案，挂谷宗一也不会过于震惊。顶多就是个之前没想到的几何图形嘛，对吧，难道谁还能整出个花儿来不成？
嗯，真就有人
整出花儿来了
。
终极鬼畜大神——贝西科维奇
这部分内容就是视频最后出现的蜜汁鬼畜图形背后的故事。
1924年，苏联数学家贝西科维奇（Abram Samoilovitch Besicovitch），因为国内革命愈演愈烈，开始了颠沛流离的生活。在满欧洲乱跑的时间段，贝西科维奇接触到了挂谷宗一
的
研究课题，很快就发现了挂谷问题和自己在1919年发表的一篇论文有着惊人的关联性（贝西科维奇：“惊人？不惊人呀。”），于是开始利用俄罗斯数学家的种族天赋（至于俄罗斯数学为什么这么NB，这里省略10万字），着手解决这个问题。
最终，在1928年，贝西科维奇给出了让人瞠目结舌的答案：“挥刀面积”可以无限小。
