导读:
线性代数往往是学习机器学习和深度学习的一大障碍,为了解决这个问题,我们特别邀请了 Udacity 机器学习&深度学习导师 Aaron,帮助大家梳理神经网络中涉及的数学知识,以及理解其物理含义。希望大家读过之后,可以使大家对于神经网络有更多角度的理解,帮助大家推导以及理解其中的数学公式。
矩阵乘以向量的物理含义
矩阵乘法我更喜欢称作线性转换。一个矩阵乘以向量中,矩阵相当于一个转换函数,而向量是一个输入,已知了输入和函数,我们就可以知道输出。这里需要强调的是,向量共有两种形式,一种为列向量,一种为行向量。在默认情况下,向量是指列向量。大部分的国内教材中,并没有特意提到这一点。很多人接触到编写代码时,都是以行向量的形式开始学习,导致后续有很多概念产生混淆。在本文中,若无特殊说明,向量的形式默认为列向量。
首先我们先看以下的2道热身题:
1. 假设读者并不知道矩阵乘法的运算准则,能否在假想的几何空间中,快速地反应出答案是多少呢?给大家30s。(记住,不可以通过运算法则来进行计算)
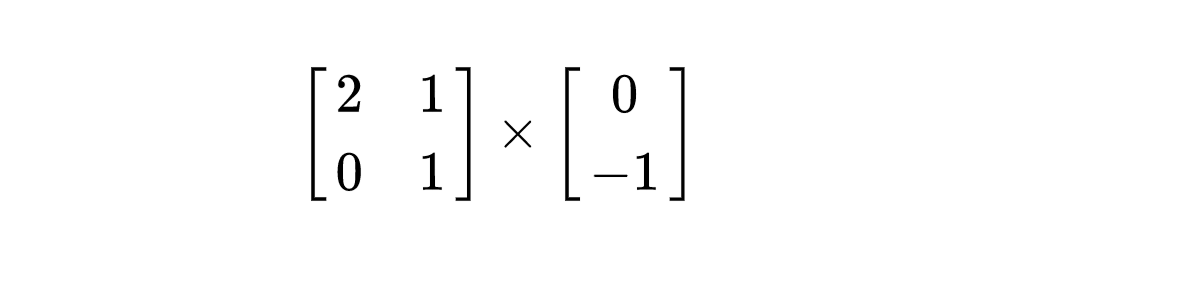
2. 同样地,利用假想的几何空间想象,是否可以立即解答出矩阵M是什么?
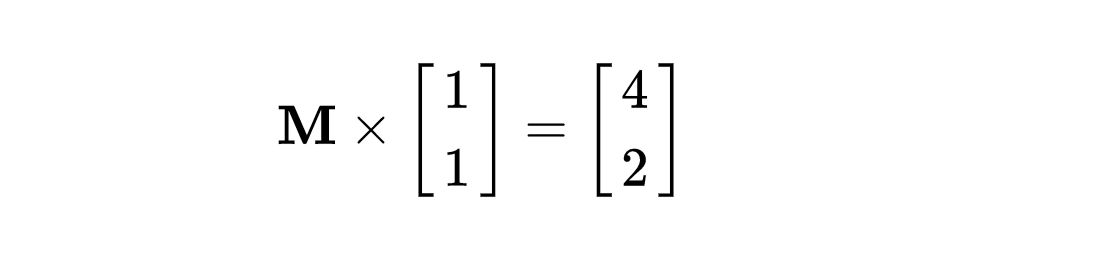
如果读者可以快速解答出上面的问题,那么恭喜您,您已经了解了线性代数空间转换的本质;如果没有解答出,那就是我写这篇文章的意义。
先抛开上面两道题,这里来介绍一下矩阵。
线性代数与空间几何是存在紧密的联系的。基本所有的线性代数都有其对应的几何表示方法。理解几何,是理解线性代数的核心所在。
以二维空间来说,举个栗子:

现在,我们来看一张动图:
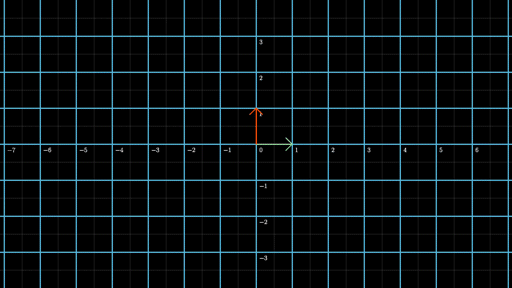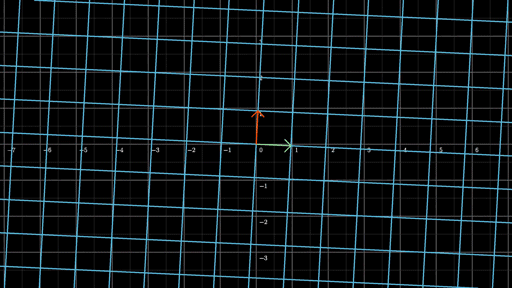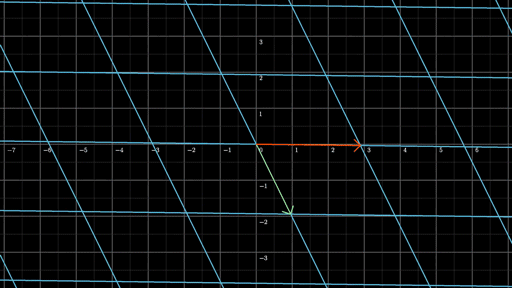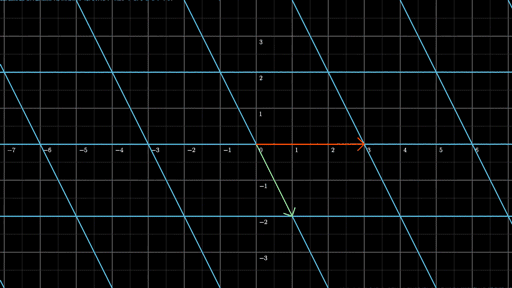
更多动图的信息请关注3Blue1Brown主页,里面有大量冲破你数学世界观的知识。3Blue1Brown还有视频集。B站有做了很赞的汉化,不过更鼓励大家去看英文原版视频。

我们来继续看看表示方法:

这其中的区别就是基向量不一样了,而线性组合的系数 -1 与 2 保持固定不变。
我们把变换后的基向量放在一起,变为矩阵:

我们在来看另一幅动图来实践一下,找到这幅动图的线性变换矩阵是什么?
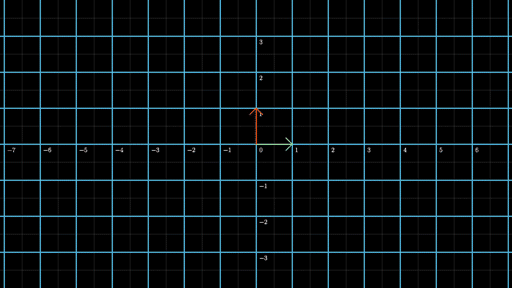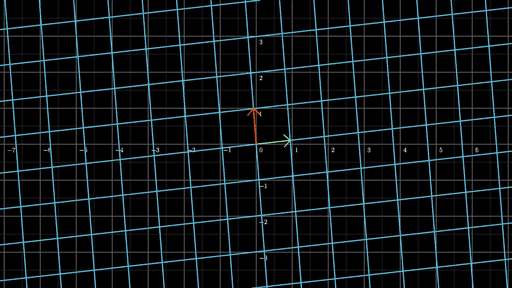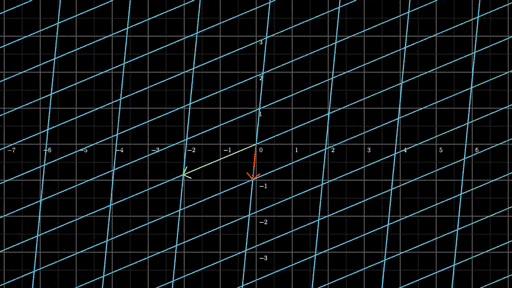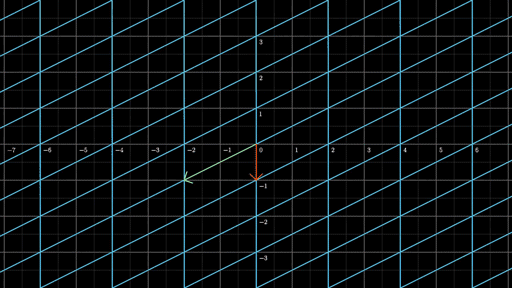
根据上面的方法,锁定绿色与红色基向量末尾的位置,这幅动图的线性变换矩阵为
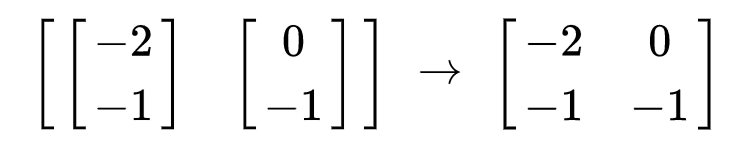
而其原来所有坐标系上的向量都随之变换发生改变。
现在再回头看看上面的两道题?是否能够通过想象的空间去快速找到答案?

如果不是方阵咋办?
上面我们讲的是方阵,那么如果不是方阵呢?比如一个 3 x 2 的矩阵,或者一个 2 x 3 的矩阵呢? (以下我们只用中括号来代表具体矩阵的形状,具体数字并不重要。)
我们来以 3 x 2 矩阵形式举例,如下所示:
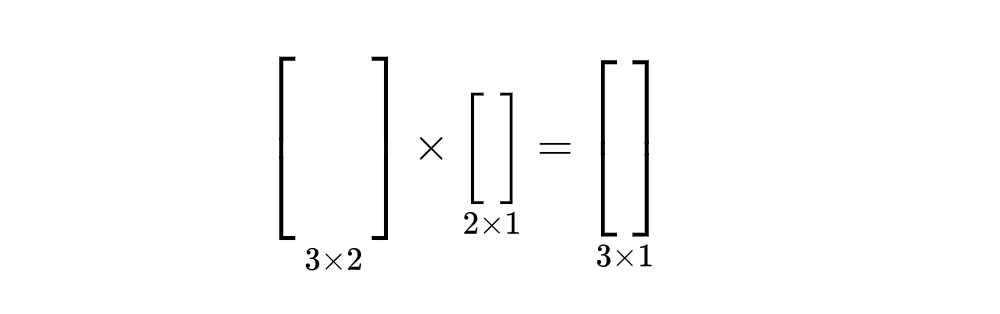
3 x 2 的矩阵的物理含义就是把一个向量从二维表示方法转换到三维表示。而转换矩阵的每一列就代表:将二维空间对应的基向量转换到三维的样子。将这种变换规律映射到其他变换的二维向量;同样地, 2 x 3 矩阵物理含义就是将一个向量从三维表示转换成二维表示。转换矩阵每一列代表:三维空间的基向量映射到二维空间之后的样子。将这种变换规律映射到其他变换的三维向量。
现在,我们再进行下一步操作。如果我们假设让一个4维向量,先转化为3维向量,在转化为二维向量,那么它的形式是什么样子的呢?
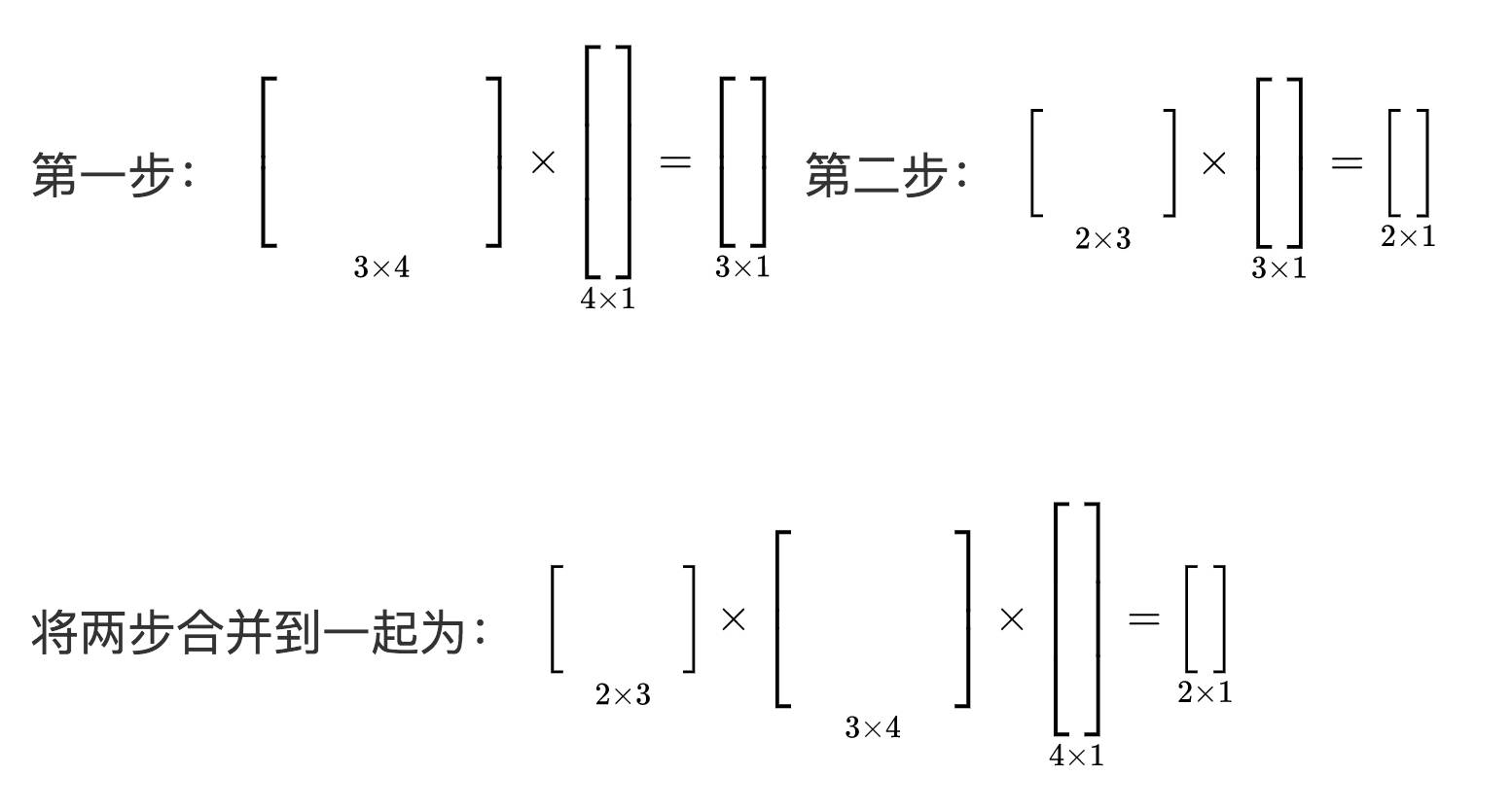
通过以上形式,我们可以发现如果将一个列向量经过多次线性转换,他的顺序应该是从右至左的顺序。这就是标准的线性代数书中所讲到的连续线性变换的形式,从右至左也是线性代数数学家习惯的顺序。
但是,在很多神经网络包括深度学习网络的课程中我们可以看到,更符合我们阅读的顺序是将一个输入数据拿进来之后经过一次矩阵转换,从左至右得到输出结果。他们之间有什么联系呢?
通过观察我们可以知道,这其中最大的原因在于数据的形式,也就是上文中提到的每一个样本表示方法是列向量还是行向量。如果是列向量,变换的顺序就是从右至左;如果是行向量,变换顺序就是从左至右。而相应的矩阵形状也发生反转。

神经网络中,大家都希望最终的形式为矩阵乘以矩阵,不希望中间有任何向量的存在,这样显得更酷,实际上计算也更快。这很简单,现在我们只差最后一步。当我们把所有数据放在一起,还是如上方有 m 个 4 维行向量形式的数据,我们将这些行向量数据堆叠在一起形成 m x 4的矩阵,经过多个矩阵的变换之后输出为一个 m x 2 的矩阵。这样,在计算过程中,全部为不同形状的矩阵。当然,大家也可以想想如果是列向量该是什么形式。
以上内容想说明的就是,无论是上方哪一种形式,都是正确的。关键看输入的数据是什么形式,形式决定了数据变换的顺序,以及设计矩阵的形状。
通过以上的形式,其实神经网络前向传导和向量在不同维度间的连续线性变换及其相似。唯一不同的一点就在于,在每次线性转换后,神经网络可以加一个非线性激活函数,使线性转换变为非线性转换。实际上,也就这么点区别。而非线性激活函数并不会改变数据的形状,对后续矩阵乘法不造成任何影响。
小结一下上面线性代数部分我们发现了什么:
线性代数中的向量默认形式是列向量。
矩阵的实质就是将坐标整体线性变换。
矩阵的组合以列向量组合在一起,其代表各自的基向量变换之后的新向量是什么。
矩阵与向量相乘,矩阵与矩阵相乘,顺序很重要,其决定权在于实际问题中样本的表达形式,是行向量还是列向量。
神经网络的前向传导与线性代数中连续对于向量的线性变换过程极其相似,只是在层与层之间多了非线性激活函数。
神经网络求的是什么?其实就是上方这么多矩阵中每一个位置的数字是多少?这就是我们最终的目的。那么如何求?这就需要微积分中链式法则的知识了。

囿于篇幅限制,微积分中链式法则的知识部分,
请感兴趣的同学扫码入群,获取完整文章,免费阅读
👇
这部分作者会用尽量少的公式,记住极少的关键点,帮助大家去顺利的推导神经网络中运用到的链式推导。
希望经过上述自己的梳理,大家对于神经网络中涉及到的数学知识有了更进一步形象化的了解。
点击[阅读原文],给自己一个成为硅谷认证机器学习工程师的机会!















