本文来源Robi Polikar英文官网。
本文中文部分由小编编译翻译完成,文章仅供学习使用,不可用于商业行为。
多分辨率分析与连续小波变换
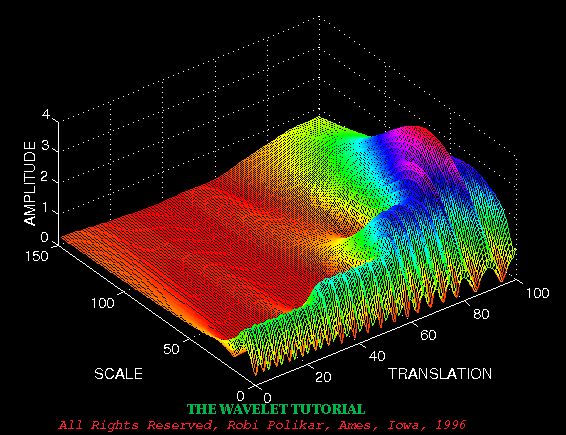
多分辨率分析
虽然时间和频率分辨率问题是物理现象(海森堡不确定性原理)的结果,并且无论使用何种变换都存在,但是可以通过使用称为
多分辨率分析(MRA)
的替代方法来分析任何信号
。
如其名称所暗示的,MRA分析具有不同分辨率的不同频率的信号。
与STFT中的情况一样,每个频谱分量都没有得到同等的解决。
MRA旨在提供高频时的良好时间分辨率和较差的频率分辨率以及良好的频率分辨率和低频时的差时间分辨率。
这种方法很有意义,特别是当手头的信号具有短持续时间的高频分量和长时间的低频分量时。
幸运的是,在实际应用中遇到的信号通常属于这种类型。
例如,以下显示了这种类型的信号。
它在整个信号中具有相对较低的频率分量,并且在中间的某个地方具有相对较高频率的分量。
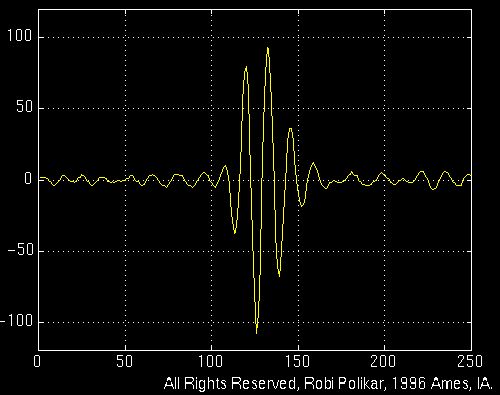
图3.1
连续小波变换
连续小波变换是作为短时傅立叶变换的替代方法而开发的,以克服分辨率问题。
小波分析以与STFT分析类似的方式完成,在某种意义上,信号乘以函数{\ it the wavelet},类似于STFT中的窗口函数,
并且变换是针对不同的单独计算的时域信号的片段
。但是,STFT和CWT之间有两个主要区别:
-
不获取加窗信号的傅立叶变换,因此将看到对应于正弦曲线的单峰,即,不计算负频率。
-
随着针对每个单个频谱分量计算变换,窗口的宽度被改变,这可能是小波变换的最重要特征。
连续小波变换定义如下
CWT_x ^ \ psi(\ tau,s)= \ Psi_x ^ \ psi(\ tau,s)= \ frac {1} {\ sqrt {| s |}} \ int x(t)\ psi ^ * \ left( \ frac {t - \ tau} {s} \ right)dt
公式3.1
如上面的等式所示,变换后的信号分别是两个变量
tau
和
s
,
平移
和
比例
参数的函数。
\ psi(t)
是转换函数,它被称为
母小波
。术语母小波得名小波分析的,由于两个重要的属性如下解释:
术语
小波
意味着
小波浪
。
小的是指这个(窗口)函数具有有限长度(
紧凑支持
)的条件。波指的是这个函数是振荡的条件。
术语
母波
意味着在转换过程中使用的具有不同支持区域的函数来自一个主函数或母小波。换句话说,
母小波是用于生成其他窗函数的
原型
。
它与窗口的位置有关,因为窗口通过信号移动。显然,该术语对应于变换域中的时间信息。但是,我们没有频率参数,正如我们之前为STFT所做的那样。相反,我们有scale参数,定义为
\ frac {1} {frequency}
。术语频率保留用于STFT。缩放在下一节中有更详细的描述。
尺度
小波分析中
的参数
比例
类似于地图中使用的比例。
与地图的情况一样,高比例对应于(信号的)非详细的全局视图,而低比例对应于详细视图。
类似地,就频率而言,低频(高音)对应于信号的全局信息(通常跨越整个信号),而高频(低音)对应于信号中隐藏模式的详细信息(这通常持续相对较短的时间)。
对应于各种比例的余弦信号作为下图中的示例给出。
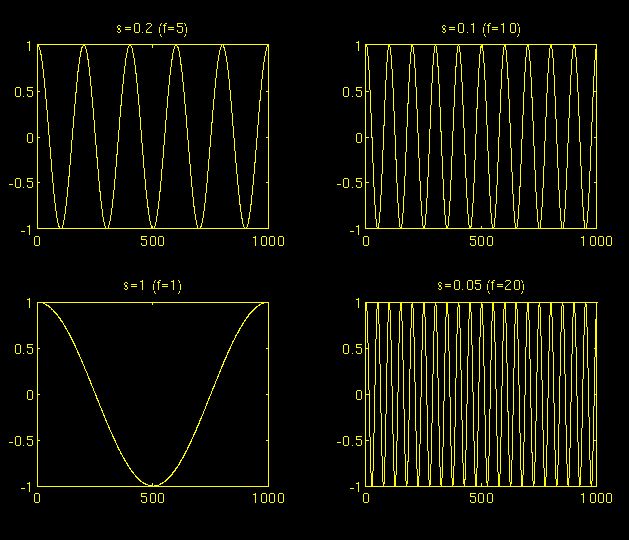
图3.2
幸运的是,
在实际应用中,低音(高频)不会持续整个信号持续时间,与图中所示不同,但它们通常不时出现短脉冲或尖峰。高音阶(低频)通常持续整个信号持续时间。
作为数学运算,缩放可以扩大或压缩信号。
较大的标度对应于扩张(或伸展)信号,小标度对应于压缩信号。
图中给出的所有信号都来自相同的余弦信号,即它们是相同函数的扩张或压缩版本。
在上图中,
s = 0.05
是最小尺度,
s = 1
是最大尺度。
在数学函数而言,如果
F(T)
是一个给定的函数
F(ST)
相对应的收缩(压缩)版本
F(T)
,
如果
S> 1
和到的扩展(扩张)版本
F(T)
,
如果
s <1
。
然而,在小波变换的定义中,缩放项用在分母中,因此,与上述陈述相反,即,比例
s> 1
扩大信号,而比例
s <1
,压缩信号。
这种解释将在本文中使用。
CWT的计算
本节将解释上述等式的解释。
设
x(t)
是要分析的信号。
选择母小波作为过程中所有窗口的原型。
使用的所有窗口都是母小波的扩张(或压缩)和移位版本。
有许多功能可用于此目的。
Morlet小波和墨西哥帽函数是两个候选者,它们用于本章后面介绍的示例的小波分析。
一旦选择了母小波,计算就以
s = 1
开始
并且对于s的所有值计算连续小波变换,小于和大于“1”。
但是,根据信号,通常不需要完整的变换。
出于所有实际目的,信号是带限的,因此,对于有限的标度间隔的变换的计算通常是足够的。
在本研究中,使用了s的一些有限的值区间,这将在本章后面描述。
为方便起见,该过程将从比例
s = 1开始
,并将继续增加s的值,即,分析将从高频开始并向低频进行。
s的第一个值将对应于压缩最小的小波。
随着s的值增加,小波将扩张。
小波被放置在信号的开头处,其对应于时间= 0。小波函数在尺度``1“”由信号相乘,然后集成点
在所有次
。
然后将积分的结果乘以常数
\ {frac {1} {\ sqrt {s}}
。
该乘法用于能量归一化目的,使得变换后的信号在每个尺度上具有相同的能量。
最终结果是变换的值,即
在零时刻
和
标度s = 1
的连续小波变换的值
。
换句话说,它是对应于点
\ boldsymbol \ tau
= 0
,
s = 1的值
在时间尺度的飞机上。
然后,尺度为
s = 1
的小波
向右移动
\ tau
量达到位置
t =
\ boldsymbol \ tau
,并且计算上述等式以获得
t = tau
处的变换值
,
s = 1
的时间 -频率平面。
重复该过程直到小波到达信号的末尾。
现在完成
了比例
s = 1
的时标平面上的一行点
。
然后,
s
增加一个小值。
请注意,这是一个连续变换,因此,
\ boldsymbol \ tau
和
s
必须连续递增。
但是,如果需要通过计算机计算此变换,则两个参数都会
以
足够小的步长增加
。
这对应于对时标平面进行采样。
对于s的每个值重复上述过程。
对于给定的s值,每次计算都填充时间尺度平面的相应单行。
当针对所有期望的s值完成该过程时,已经计算了信号的CWT。
下图逐步说明了整个过程。
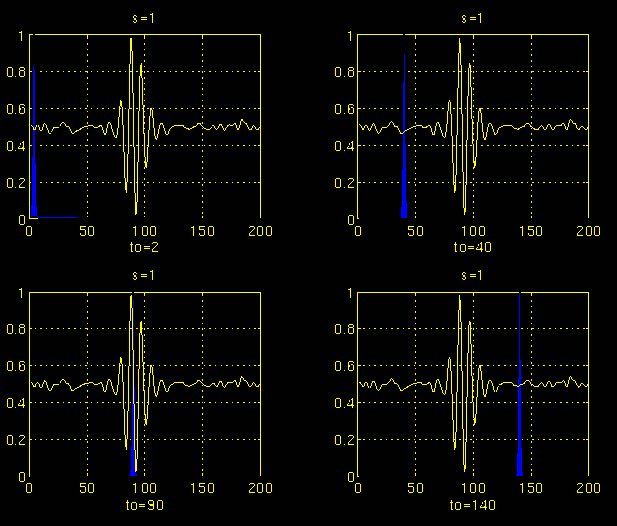
图3.3
在图3.3中,信号和小波函数显示了
\ boldsymbol \ tau的
四个不同值
。
该信号是图3.1中所示信号的截断版本。
比例值为
1
,对应于最低比例或最高频率。
注意它是多么紧凑(蓝色窗口)。
它应该与信号中存在的最高频率分量一样窄。
小波函数的四个不同位置如图所示:
\ boldsymbol {t_o}
= 2,
\ boldsymbol {t_o}
= 40,
\ boldsymbol {t_o}
= 90,
\ boldsymbol {t_o}
= 140
。
在每个位置,它乘以信号。
显然,只有当信号落在小波支持区域时,才是非零的,而在其他地方则为零。
通过及时移动小波,信号在时间上定位,并且通过改变s的值,信号被定位在比例(频率)中。
如果信号的光谱分量对应于s的当前值(在这种情况下为1),则小波与
该光谱分量存在的位置处
的信号的乘积
给出了一个相对较大的值。
如果信号中不存在对应于s的当前值的频谱分量,则乘积值将相对较小或为零。
图3.3中的信号具有与
s = 1时
窗口宽度相当的光谱分量,
大约为
t = 100 ms
。
图3.3中信号的连续小波变换将在100 ms左右的时间内产生较大的低尺度值,在其他地方产生较小的值。
另一方面,对于高比例,连续小波变换将在几乎整个信号持续时间内给出大的值,因为始终存在低频。
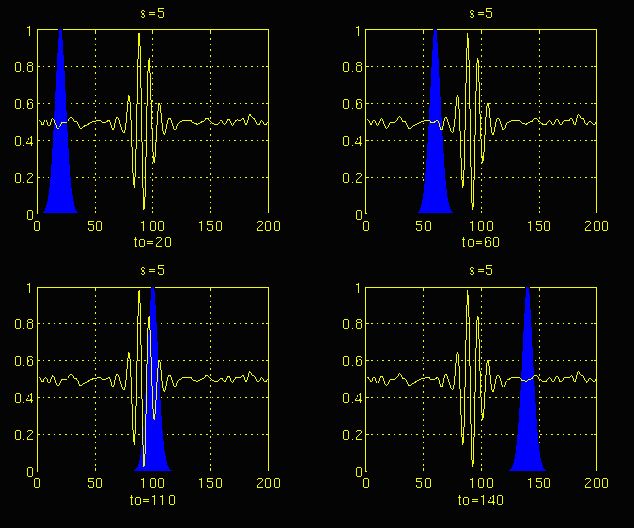
图3.4
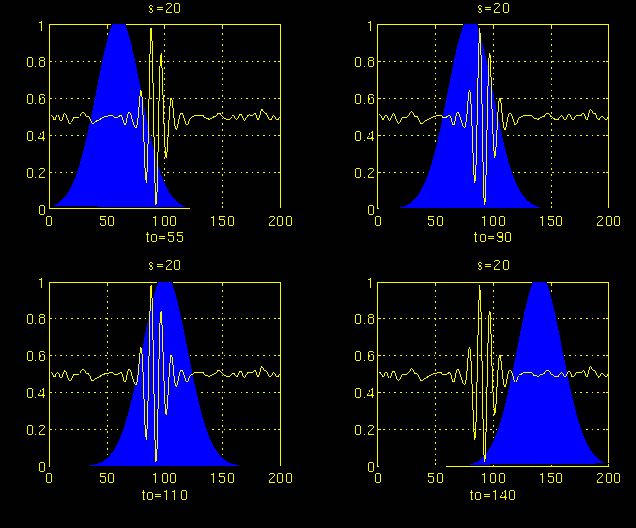
图3.5
图3.4和3.5分别说明了尺度s = 5和s = 20的相同过程。
注意窗口宽度如何随着比例增加而变化(降低频率)。
随着窗口宽度的增加,变换开始拾取较低频率的分量。
结果,对于每个尺度和每个时间(间隔),计算时间尺度平面的一个点。
一个尺度的计算构造时间尺度平面的行,并且不同尺度的计算构造时间尺度平面的列。
现在,让我们看一个例子,看看小波变换的真实情况。
考虑
非平稳
信号如图3.6所示。
这类似于STFT给出的示例,除了在不同的频率。
如图所示,信号由30 Hz,20 Hz,10 Hz和5 Hz的四个频率分量组成。
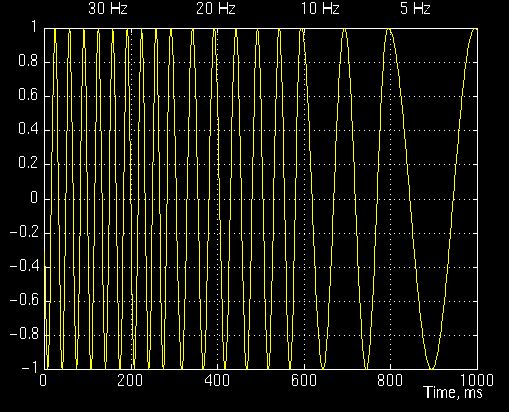
图3.6
图3.7是该信号的连续小波变换(CWT)。
请注意,轴是平移和缩放,而不是时间和频率。
母小波的转换可以被认为是自
t = 0
以来经过的时间
。
然而,尺度有着完全不同的刻度。
请记住,公式3.1中的
比例参数s实际上是频率的倒数
。
换句话说,无论我们所说的关于频率分辨率的小波变换的特性,它的倒数将出现在显示时域信号的WT的图中。

图3.7
请注意,在图3.7中,较小的比例对应于较高的频率,即频率随着比例增加而减小,因此,图表中具有零附近的比例的部分实际上对应于分析中的最高频率,而具有高比例的那部分对应于最低频率。频率。
请记住,信号首先具有30 Hz(最高频率)分量,并且在0到30的平移时出现在最低比例。然后是20 Hz分量,第二高频率,依此类推。
5 Hz分量出现在平移轴的末端(如预期的那样),并且在更高的标度(低频率)处出现,如预期的那样。
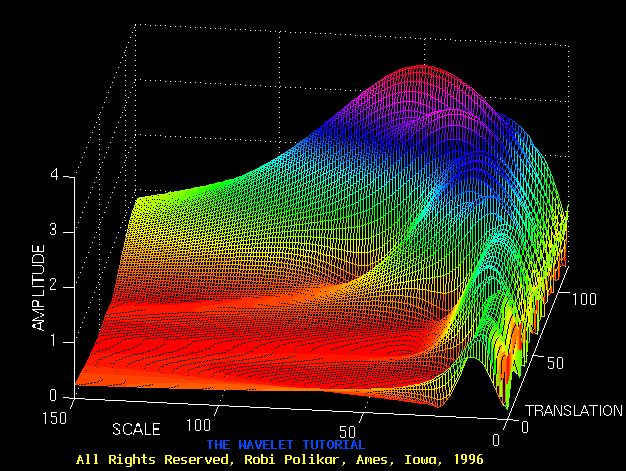
图3.8
现在,回想一下这些分辨率属性:
与在任何时间和频率都具有恒定分辨率的STFT不同,WT在高频时具有良好的时间和差的频率分辨率,并且在低频时具有良好的频率和差的时间分辨率。
图3.8从另一个角度显示了图3.7中相同的WT,以更好地说明分辨率属性:在图3.8中,较低的比例(较高频率)具有
更好的比例分辨率
(比例更窄,这意味着它的含义更不明确对应于
较差频率
的比例)
解析度 。
类似地,更高的尺度具有尺度频率分辨率(更大的尺度支持),这对应于较低频率的更好的频率分辨率。
图3.7和3.8中的轴是标准化的,应进行相应的评估。
粗略地说,平移轴上的100个点对应于1000毫秒,刻度轴上的150个点对应于40 Hz的频带(平移轴和刻度轴上的数字
分别
不对应
于秒和Hz,它们只是计算中的样本数量)。
时间和频率分辨率
在本节中,我们将仔细研究小波变换的分辨率属性。
请记住,解决问题是我们从STFT切换到WT的主要原因。
图3.9中的图通常用于解释如何解释时间和频率分辨率。
图3.9中的每个框对应于时频平面中的小波变换值。
注意,框具有某个
非零
区域,这意味着无法知道时频平面中特定点的值。
落入框中的时频平面中的所有点由WT的一个值表示。
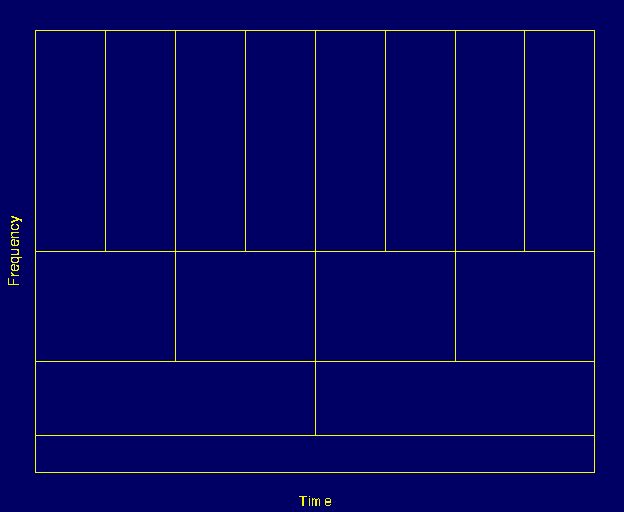
图3.9
让我们仔细看看图3.9:首先要注意的是,虽然框的宽度和高度发生了变化,但面积是不变的。
也就是说,
每个框表示时频平面的相等部分,但是给出时间和频率的不同比例。
请注意,在低频时,框的高度较短(这对应于更好的频率分辨率,因为关于精确频率的值的模糊性较小),但它们的宽度较长(这对应于较差的时间分辨率,因为那里关于确切时间的价值更加含糊不清)。
在较高频率处,框的宽度减小,即时间分辨率变得更好,并且盒子的高度增加,即频率分辨率变差。
在结束本节之前,值得一提的是在STFT的情况下分区是怎样的。
回想一下,在STFT中,时间和频率分辨率由分析窗口的宽度确定,分析窗口的宽度在整个分析中被选择一次,即时间和频率分辨率都是恒定的。
因此,时频平面由
STFT情况下
的
正方形
组成
。
无论框的尺寸如何,STFT和WT中所有框的面积都是相同的,并由
Heisenberg的不等式
决定
。
总之,对于每个窗口函数(STFT)或母小波(CWT),框的区域是固定的,而不同的窗口或母小波可以导致不同的区域。
然而,
所有区域都以
\ boldsymbol {\ frac {1} {4} \ pi}为界
。
也就是说,由于海森堡的不确定性原理,我们无法根据需要减少箱子的面积。
另一方面,对于给定的母小波,可以改变框的尺寸,同时保持区域相同。
这正是小波变换所做的。
小波理论:一种数学方法
本节描述了小波分析理论的主要思想,它也可以被认为是大多数信号分析技术的基本概念。
傅立叶定义的FT使用
基函数
来分析和重构函数。
矢量空间中的每个矢量可以写为该矢量空间中的基矢量的线性组合
,即,通过将矢量乘以某个常数,然后乘以乘积的总和。
信号的分析涉及这些常数的估计(变换系数,或傅里叶系数,小波系数等)。
合成或重建对应于计算线性组合方程。
这进一步阐明了先前关于信号与小波在一定范围内的相关性的讨论。
如果信号具有与当前标度对应的频率的主要分量,则当前标度处的小波(基函数)将
相似
或
接近
在该频率分量出现的特定位置处的信号。
因此,在时间尺度平面中此时计算的CWT系数将是相对大的数量。
在我们结束本节之前,我想包括两个常用于小波分析的母小波。
墨西哥帽小波被定义为高斯函数的二阶导数:
w(t)= \ frac {1} {\ sqrt {2 \ pi} \ cdot \ sigma} e ^ {\ frac {-t ^ 2} {2 \ sigma ^ 2}}
公式3.15
\ psi(t)= \ frac {1} {\ sqrt {2 \ pi} \ cdot \ sigma ^ 3} \ left(e ^ {\ frac {-t ^ 2} {2 \ sigma ^ 2}} \ cdot \ left(\ frac {t ^ 2} {\ sigma ^ 2} - 1 \ right)\ right)
公式3.16
Morlet小波定义为
w(t)= e ^ {iat} \ cdot e ^ { - \ frac {t ^ 2} {2 \ sigma}}
公式
3.16_a
其中
a
是调制参数,
sigma
是影响窗口宽度的缩放参数。
例子
下面给出的所有示例都对应于现实生活中的非平稳信号。
这些信号来自数据库信号,包括
正常人和阿尔茨海默病患者的
事件相关电位
。
由于这些不是像简单正弦曲线那样的测试信号,因此解释它们并不容易。
这里展示的只是为了了解真实生活中CWT的外观。
图3.11所示的以下信号属于普通人。
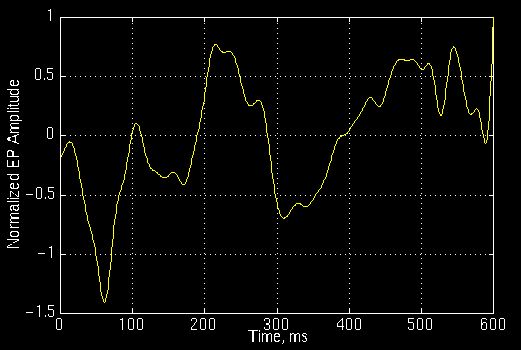
图3.11
以下是其CWT。
轴上的数字对我们来说并不重要。
这些数字只是表明CWT是在平移比例平面上的350个平移位置和60个标度位置计算的。
这里要注意的重点是计算不是真正的
连续
WT,因为从有限数量的位置计算可以明显看出。
这只是CWT的离散化版本,本页稍后将对此进行说明。但请注意,这不是离散小波变换(DWT)
,它是本教程第四部分的主题。
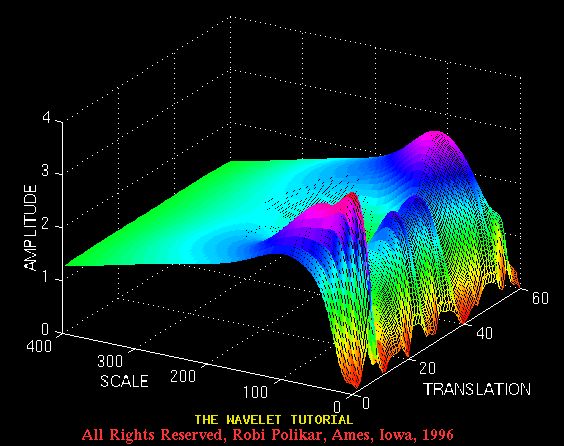
图3.12
图3.13绘制了从不同角度进行的相同变换,以获得更好的可视化效果。
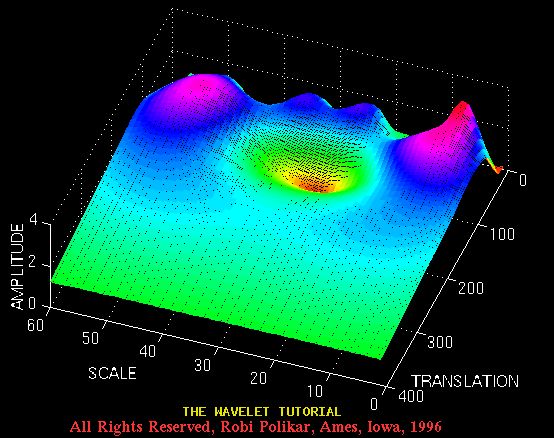
图3.13
图3.14描绘了被诊断患有阿尔茨海默病的患者的事件相关电位
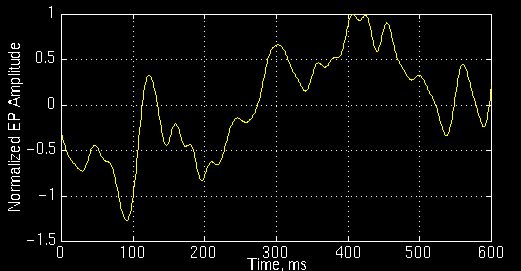
图3.14
图3.15说明了它的CWT:
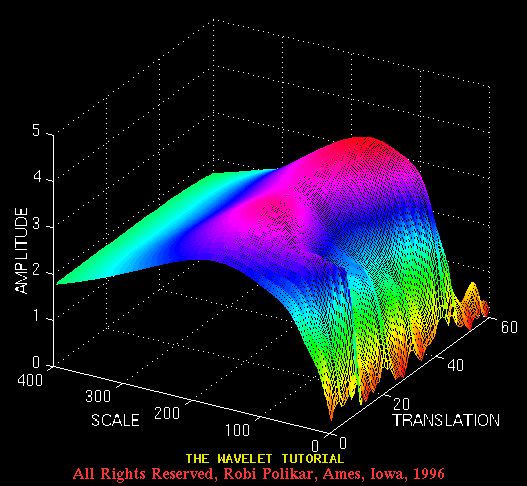
图3.15
这是另一种不同角度的观点
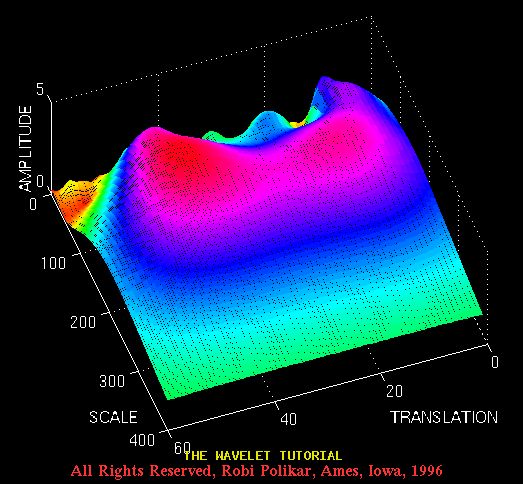
图3.16
小波合成
连续小波变换是可逆变换,只要满足公式3.18即可。
幸运的是,这是一个非常非限制性的要求。
如果满足等式3.18,则连续小波变换是可逆的,即使基函数通常可能不是正交的。
通过使用以下重建公式可以进行重建:
x(t)= \ frac {1} {C_ \ psi ^ 2} \ int_s \ int_ \ tau \ left [\ Psi ^ \ psi_x(\ tau,s)\ frac {1} {s ^ 2} \ psi \ left(\ frac {t - \ tau} {s} \ right)\ right] d \ tau \ cdot ds
Equation 3.17
其中
C_ \ psi
是一个取决于所用小波的常数。
重建的成功取决于这个常数,即可
容许性常数
,以满足以下
可接受性条件
:
C_ \ psi = \ left \ {2 \ pi \ int _ { - \ infty} ^ {\ infty} \ frac {| \ hat {\ psi}(\ xi)| ^ 2} {| \ zeta |} d \ xi \ right \} ^ {\ frac {1} {2}}
Equation 3.18
其中
\ hat {\ psi}(\ xi)
是
\ psi(t)
的FT
。
公式3.18暗示
\ hat {\ psi}(0)= 0
,即
\ int \ psi(t)\ cdot dt = 0
公式3.19
如上所述,公式3.19不是非常严格的要求,因为可以找到许多小波函数,其积分为零。
对于满足公式3.19,小波必须是振荡的。
连续小波变换的离散化:小波系列
在今天的世界中,计算机被用来进行大多数计算(好吧,......好吧......几乎所有的计算)。


















