(点击上方蓝字,快速关注我们)
来源:伯乐在线专栏作者 - 路易十四
如有好文章投稿,请点击 → 这里了解详情
任务需求:现有140w个某地区的ip和经纬度的对应表,根据每个ip的/24块进行初步划分,再在每个区域越100-200个点进行细致聚类划分由于k值未知,采用密度的Mean Shift聚类方式。
0#目录:
1#原理部分
关于kmeans纯代码实现可以移步之前的一篇
机器学习-聚类算法-k-均值聚类-python详解
在文中已经对代码做了详细的注释。
介绍
K-means算法是是最经典的聚类算法之一,它的优美简单、快速高效被广泛使用。它是很典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
图示
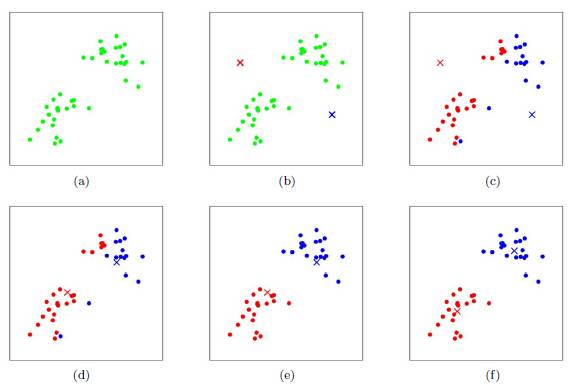
步骤
从N个点随机选取K个点作为质心
对剩余的每个点测量其到每个质心的距离,并把它归到最近的质心的类
重新计算已经得到的各个类的质心
迭代2~3步直至新的质心与原质心相等或小于指定阈值,算法结束
优点
k-平均算法是解决聚类问题的一种经典算法,算法简单、快速。
对处理大数据集,该算法是相对可伸缩的和高效率的,因为它的复杂度大约是O(nkt),其中n是所有对象的数目,k是簇的数目,t是迭代的次数。通常k
算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的,而簇与簇之间区别明显时,它的聚类效果很好。
缺点
K 是事先给定的,这个 K 值的选定是非常难以估计的;
对初值敏感,对于不同的初始值,可能会导致不同的聚类结果。一旦初始值选择的不好,可能无法得到有效的聚类结果;
该算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是非常大的。
不适合于发现非凸面形状的簇,或者大小差别很大的簇;
对于”噪声”和孤立点数据敏感,少量的该类数据能够对平均值产生极大影响。
关于K值的确定主要在于判定聚合程度:提供几篇论文注意,这些论文仅仅是提供思路,不要去自己写出来,内容有点扯
2#框架资源
本次基于密度的kmeans算法使用的是 scikit-learn 框架。
官网:http://scikit-learn.org/stable/index.html
聚类算法汇总:http://scikit-learn.org/stable/modules/clustering.html
KMeans算法 : http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_assumptions.html#sphx-glr-auto-examples-cluster-plot-kmeans-assumptions-py
MeanShift算法: http://scikit-learn.org/stable/modules/generated/sklearn.cluster.MeanShift.html#sklearn.cluster.MeanShift
meanShift 测试demo:http://scikit-learn.org/stable/auto_examples/cluster/plot_mean_shift.html#sphx-glr-auto-examples-cluster-plot-mean-shift-py
安装框架环境:http://scikit-learn.org/stable/install.html
测试数据集合下载:data 数据比较小,百来个经纬度的点
3#实践操作
3.1:运用 Kmeans 使用2-6作为k值评定聚类效果
。请先下载上文中的数据集合,和测试代码放在同一目录下,确保下列运作环境已经安装完成:
完整运行代码:请结合官方文档,可以理解运行的参数和返回值
from sklearn.cluster import KMeans
from sklearn.externals import joblib
import numpy
import matplotlib.pyplot as plt
# -*- coding: utf-8 -*-
from sklearn.cluster import KMeans
from sklearn.externals import joblib
import numpy
import time
import matplotlib.pyplot as plt
if __name__ == '__main__':
## step 1: 加载数据
print "step 1: load data..."
dataSet = []
fileIn = open('./data.txt')
for line in fileIn.readlines():
lineArr = line.strip().split(' ')
dataSet.append([float(lineArr[0]), float(lineArr[1])])
#设定不同k值以运算
for k in range(2,10):
clf = KMeans(n_clusters=k) #设定k !!!!!!!!!!这里就是调用KMeans算法
s = clf.fit(dataSet) #加载数据集合
numSamples=len(dataSet)
centroids = clf.labels_
print centroids,type(centroids) #显示中心点
print clf.inertia_ #显示聚类效果
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ', 'pr']
#画出所有样例点 属于同一分类的绘制同样的颜色
for i in xrange(numSamples):
#markIndex = int(clusterAssment[i, 0])
plt.plot(dataSet[i][0], dataSet[i][1], mark[clf.labels_[i]]) #mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ', 'pb']
# 画出质点,用特殊图型
centroids = clf.cluster_centers_
for i in range(k):
plt.plot(centroids[i][0], centroids[i][1], mark[i], markersize = 12)
#print centroids[i, 0], centroids[i, 1]
plt.show()
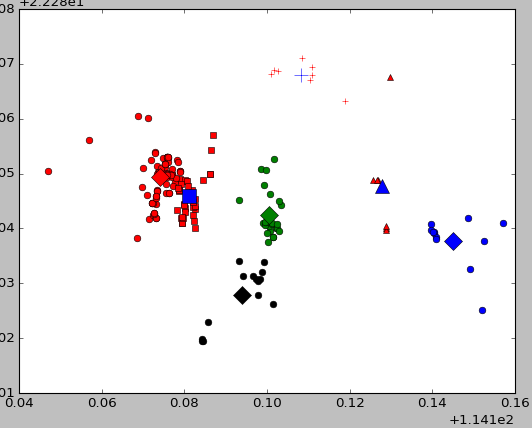
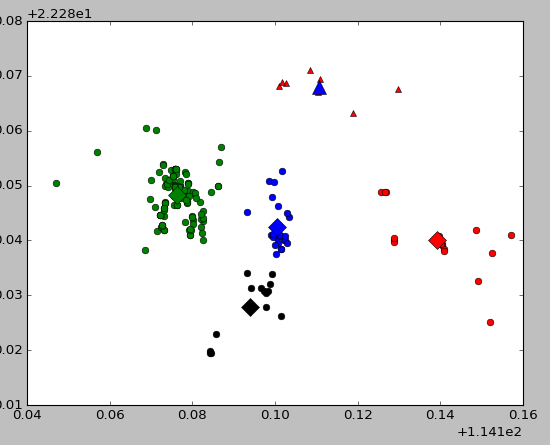
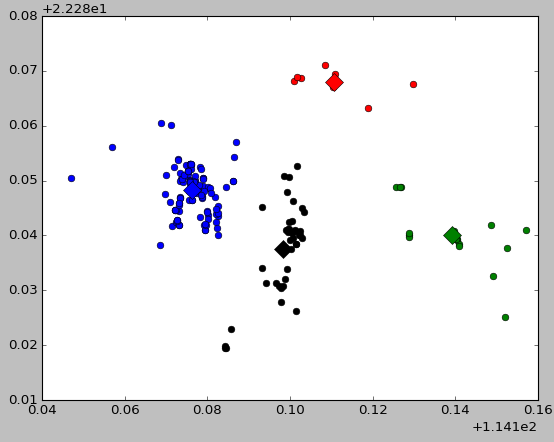
效果截图如下:
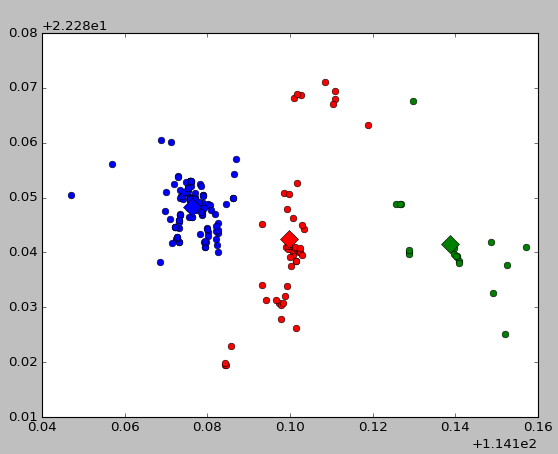
3.1:使用MeanShift自动生成k值删除游离点
注意此部分中数据集合需要转换为np.array类型。
# -*- coding: utf-8 -*-
from sklearn.cluster import KMeans
from sklearn.externals import joblib
import numpy ,time
import matplotlib.pyplot as plt
from sklearn.cluster import MeanShift, estimate_bandwidth
import numpy as np
if __name__ == '__main__':
## step 1: 加载数据
print "step 1: load data..."
dataSet = []
fileIn = open('./data.txt')
for line in fileIn.readlines():
lineArr = line.strip().split(' ')
dataSet.append([float(lineArr[0]), float(lineArr[1])])
numSamples = len(dataSet)
X = np.array(dataSet) #列表类型转换成array数组类型
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)
clf = MeanShift(bandwidth=bandwidth, bin_seeding=True,cluster_all=True).fit(X)
centroids = clf.labels_
print centroids,type(centroids) #显示每一个点的聚类归属
# 计算其自动生成的k,并将聚类数量小于3的排除
arr_flag = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
for i in clf.labels_:
arr_flag[i]+=1
k = 0
for i in arr_flag:
if(i > 3):
k +=1
print k
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ', 'pr']
#画出所有样例点 属于同一分类的绘制同样的颜色
for i in xrange(numSamples):
plt.plot(dataSet[i][0], dataSet[i][1], mark[clf.labels_[i]]) #mark[markIndex])
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', ', 'pb']
# 画出质点,用特殊图型
centroids = clf.cluster_centers_
for i in range(k):
plt.plot(centroids[i][0], centroids[i][1], mark[i], markersize = 12)
print centroids #显示中心点坐标
plt.show()
运行截图如下:

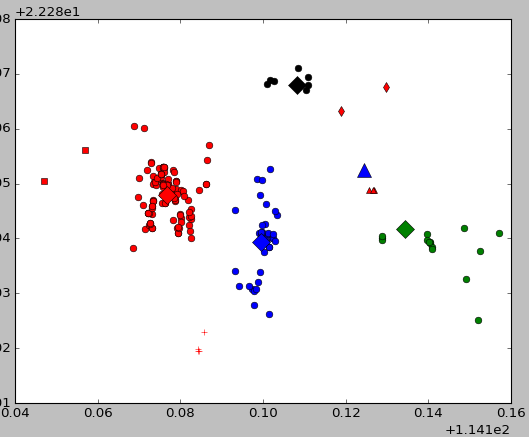
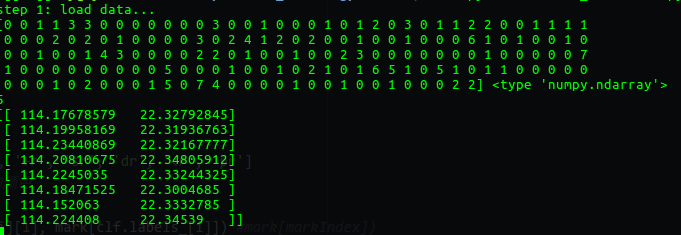
其中第一部分是每一个点在聚类之后所属的类的标识,可以看出最高有7,说明该集合最多聚集了8个类,显示的数值为5则是聚类中类数目大于3的有5个。
关于项目最后
140w个经纬数据,按照ip/24分类,分出19660个24块,对每一个24块聚类,将分类结果和游离点标记,重新写回数据库,项目完结。
总计运算时间约半小时。其实聚类耗时少,测试时时间主要消耗在绘图上。曾经直接将10000个点一起聚类,但是在大的距离尺度下,密度的衡量值就变化了,导致10000个点只分出10个类别,导致精度不和要求所以拆分块之后再聚类。
看完本文有收获?请转发分享给更多人
关注「Python开发者」,提升Python技能
















