一对夫妻
两位“老耶路撒冷人”
历时十年
用心与泪撰写出
十二册耶路撒冷当地指南
给你提供一套完美的徒步方案
通过脚的丈量
感受圣城三千年的魅力
本文经公众号「机器人圈」授权转载（微信号：ROBO_AI）
哲学园鸣谢
图：pixabay
原文来源：intuitionmachine
作者：Carlos E. Perez
「机器人圈」编译：嗯~阿童木呀、多啦A亮
深度学习只能使用实数，难道没有人觉得这很奇怪吗？或者说，如果深度学习使用复数（注意：具有虚数的那种数字）的话，这就更奇怪了？一个可行的论据是，大脑在计算过程中使用复数的可能性是非常低的。但是，你也可以提出这样的一个论据，大脑是不会执行矩阵乘法或链式法则的。此外，人工神经网络（ANN）具有实际神经元的模型。而我们在很久以前就用实数分析（即具有实数变量的函数理论）代替了生物学上的合理性。
但是，为什么我们甚至一度地停止实数分析呢？我们已经把激进的现实主义都押宝在线性代数和微分方程上了，我们不妨也把所有的东西放在一起，用更广的角度来分析一下复变函数。也许复变函数论的复杂世界将给予我们更为强大的方法。毕竟，如果它适用于量子力学，那么它也许可能同样适用于深度学习。此外，深度学习和量子力学都是关于信息处理的科学，两者可能是同样的事物。
所以出于论据的考虑，让我们把任何有关生物合理性的需要的想法搁置起来。这是一个古老的论据，在1957年弗兰克•罗森布拉特（Frank Rosenblatt）提出第一个ANN的时候就已经通过了。那么问题就是，深度学习中复数能够提供哪些实数无法提供的呢？
其实，在过去的几年中，已经有几篇论文探讨了深度学习中复数的使用。但令人惊讶的是，他们中的大多数从未纳入经同行评议的杂志中。深度学习正统还只是流行于学科中。不过我们可以来回顾一下这些有趣的论文。
DeepMind有一篇文章《组合长短期记忆网络》（https://arxiv.org/abs/1602.03032）（Ivo Danihelka，Greg Wayne，Benigno Uria，Nal Kalchbrenner，Alex Graves），探讨了用于组合记忆的复数的使用。该系统用于增加LSTM的记忆。该研究的结论是，使用复数可以提供更高的记忆容量网络。而在数学方面的折衷是，相较于使用实数，使用复数需要更小的矩阵。下图显示了在记忆成本中存在的可衡量的差异（与传统LSTM相比）：
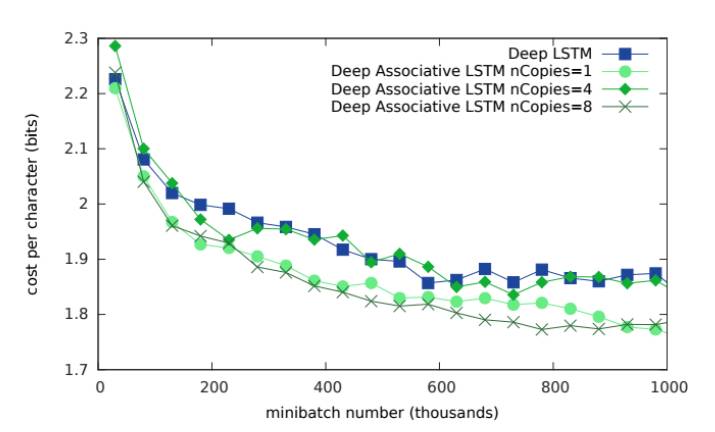
Yoshua Bengio及其在蒙特利尔的团队探讨了复数的使用的另一个领域。在一篇题为《循环神经网络的酉演化》（https://arxiv.org/pdf/1511.06464v4.pdf）（Martin Arjovsky，Amar Shah，Yoshua Bengio）的论文中，研究人员探索了酉矩阵（Unitary matrices）。他们认为，如果一个矩阵的特征值接近1，那么在减少梯度消失方面可能会有真正的好处。在这项研究中，他们探索将复数的使用作为RNN网络的权重。这项研究的结论是：
经验证据表明，我们的uRNN能够更好地通过长序列传递梯度信息，并且不会像LSTM那样遭受饱和隐藏状态的影响。
他们采取多项措施来量化这些行为VS更为传统的RNN：
使用复数值的系统显然具有更强大的鲁棒性和更为稳定的表现。
还有一篇涉及Bengio的团队和麻省理工学院人员（Li Jing、Caglar Gulcehre、Caglar Gulcehre、Caglar Gulcehre、Caglar Gulcehre、Bengio、Bengio)）的文章使用“门控机制（Gating mechanism）”方法。论文《门控正交循环单元：学习遗忘》（又名GORU）探讨了长期依赖性关系被更好地捕获的可能性，并且这可以导致一个更具鲁棒性的遗忘机制。在下图中，它们将显示在复制任务中失败的其他基于RNN的系统：
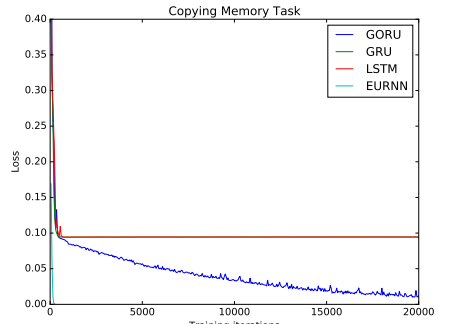
FAIR和EPFL（Cijo Jose，Moustpaha Cisse和Francois Fleuret）的一个团队也有类似的文章，在《Kronecker循环单元》（https://arxiv.org/pdf/1705.10142v2.pdf）中，他们还使用酉矩阵来显示复制任务的可行性。它们揭示了一种矩阵分解的方法，大大减少了所需参数的使用。本文介绍了他们使用复数值的动机。
由于行列式是一个连续的函数，所以在实际空间中的酉子集（unitary set）被断开。因此，使用实值网络，我们不能使用标准的连续优化程序来跨越整个单一集合。相反，酉子集在复杂的空间中连接，因为它的决定因素是单位圆上的点，而我们没有这个问题。
这篇文章的其中一个亮点就是这个非常有见地的架构理念：
状态应该保持高维，可以使用高容量网络将输入编码到内部状态，并提取预测值，但是循环动态本身可以并且应该用低容量模型来实现。
到目前为止，这些方法已经探索了RNN中复杂值的使用。来自MILA《深度复杂网络》（https://arxiv.org/pdf/1705.09792v1.pdf）（Chiheb Trabelsi等人）最近的一篇文章进一步探讨了在卷积网络中使用的方法。 作者在视觉任务中测试他们的网络，产生具有竞争力的结果。
