
原文来源
:arXiv
作者:
Andreas Groll、Christophe Ley、Gunther Schauberger、Hans Van Eetvelde
「雷克世界」编译:嗯~阿童木呀
导语:令广大球迷兴奋的2018年俄罗斯世界杯即将开始,对于球迷来说,每一届世界杯中,除了球员精湛的球技之外,惹人关注的还有对夺冠球队的预测。最近,多特蒙德工业大学(Technische Universität Dortmund)的Andreas Groll教授,根特大学(Ghent University)的Christophe Ley教授、Hans Van Eetvelde教授,慕尼黑理工大学(Technical University of Munich)的Gunther Schauberger教授比较了一些足球比赛得分的建模方法,并使用一种基于随机(决策)森林的建模方法,使用国际足联的排名,平均年龄和冠军联赛球员数量,国家人口比率,国内生产总值,甚至教练的国籍等因素,对2018年世界杯足球赛进行预测。
在这项研究中,我们比较了三种不同的足球比赛得分的建模方法,而这是根据它们在2002年至2014年四次国际足球联盟世界杯(FIFA World Cups)的所有比赛中进行的预测性表现进行的:泊松回归模型(Poisson regression models),随机森林(random forests)和排名方法(ranking methods)。前两种方法基于团队的协变量信息,而后一种方法估计足够的能力参数,而这些参数反映了当前团队的最佳实力。在这个比较中,在训练数据中表现最好的预测方法是排名方法和随机森林。然而,我们表明,通过将随机森林与来自排名方法的团队能力参数相组合作为附加的协变量,我们可以大大提高预测能力。最后,我们选择这种方法的组合作为最终模型,根据其估计,2018年世界杯将会被反复模拟,并获得所有参赛队伍的获胜概率。较之卫冕冠军德国,该模型略微偏向支持西班牙。此外,我们提供了所有球队在所有锦标赛阶段的生存概率以及最可能的锦标赛结果。
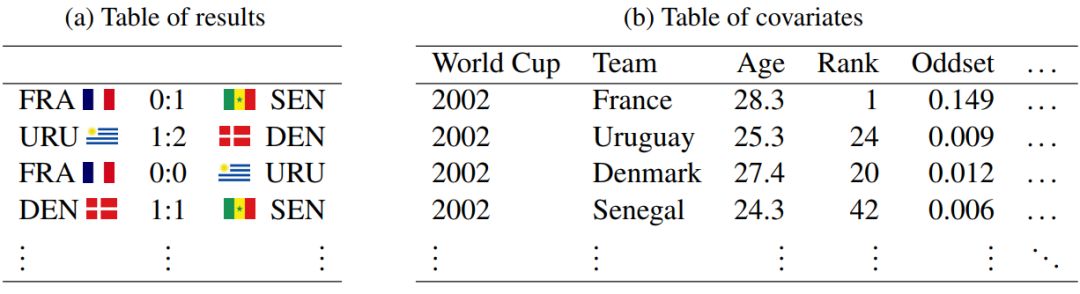
图1:样本表格显示了所涉及的团队的四组比赛和部分协变量的结果
就像之前的2014年世界杯一样,即将在俄罗斯举办的世界杯也引起了若干位建模师们的注意,他们试图预测出锦标赛的冠军。有一种方法已经为过去欧洲锦标赛(欧洲杯)和国际足联世界杯若干项赛事取得了合理的结果,这种方法是基于赌注登记经纪人(bookmakers)的几率中所包含的预期信息(Leitner、Zeileis和Hornik于2010年、Zeileis、Leitner和Hornik于2012年、2014年、2016年提出)。现在,对于这样的重要赛事,赌注登记经纪人在锦标赛开始之前为获胜者提供一个赌注。通过将若干家在线赌注登记经纪人的获胜几率汇总并将其转化为获胜概率,反向锦标赛模拟可用于计算特定于团队的能力,关于这一点可参阅Leitner、Zeileis和Hornik(于2010年提出)的论文。凭借球队特有的能力,所有单场比赛都可以通过配对比较进行模拟,因此,获得了完整的锦标赛课程。Zeileis、Leitner和Hornik(于2018年)预测巴西将以16.6%的概率赢得2018年世界杯,其次是德国(15.8%)和西班牙(12.5%)。
同样的三支球队被瑞士银行UBS的一组专家确定为最受欢迎的球员,但具有不同的概率和不同的顺序(Audran、Bolliger、Kolb、Mariscal和Pilloud,2018年):他们获得德国最受喜爱的球员,获胜概率为24.0%,其次是巴西(19.8%)和西班牙(16.1%)。他们使用一个基于四个因素的统计模型,而这四个因素将表明球队在比赛期间的表现将如何:Elo评分,球队在世界杯之前资格赛中的表现,球队在前几届世界杯锦标赛中的成绩和家庭优势。该模型通过使用前五场比赛的结果进行校准,并进行10,000次蒙特卡罗模拟(Monte Carlo simulations)以确定所有球队的获胜概率。

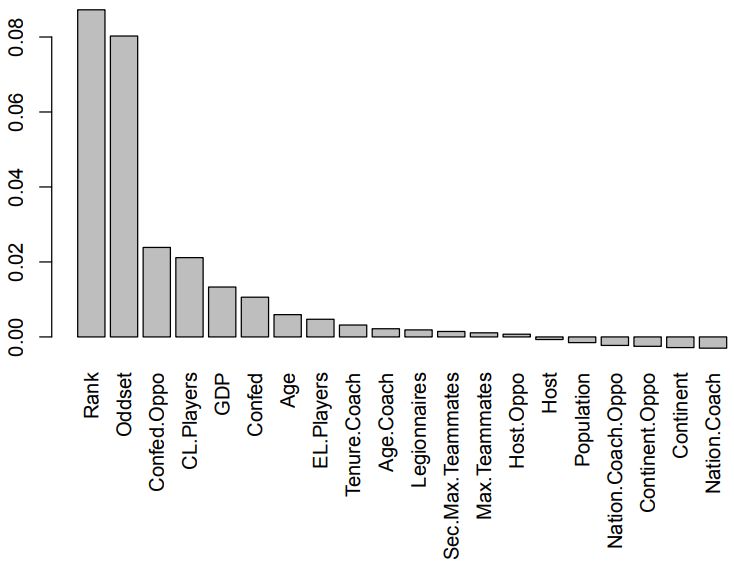
图2:条形图显示了,应用于FIFA世界杯2002—2014年数据中的随机森林中变量重要性,得分数量用作响应变量,论文第2部分描述的变量用作预测变量。
另一个被证明在预测之前的国际足球锦标赛(如欧洲杯或世界杯)结果中有价值的模型类,是泊松回归模型的类,它直接对两个竞争团队在单场比赛中的进球得分进行建模。设在i和j队之间的比赛中,Xi j和Yi j分别表示第一和第二队的目标,其中i,j∈{1,...,n},n代表锦标赛中球队的总数。假设Xi j〜Po(λij)和Yi j〜Po(μij),其中λij和μij表示相应泊松分布的强度参数(即期望的目标数量)。对于这些强度参数,存在几种建模策略,它们以不同方式将竞争团队的能力或协变量包括在内。
在最简单的情况下,泊松分布被视为(条件性)独立的,主要取决于团队的能力或协变量。例如,Dyte和Clarke(于2000年)将此模型应用于国际足联世界杯的数据中,并让两支参赛队伍的泊松强度取决于他们的国际足联排名。Groll和Abedieh(于2013年)以及Groll、Schauberger和Tutz(于2015年)分别对欧洲杯和世界杯数据分别考虑了一组潜在的有影响的变量,并使用L1惩罚方法来检测相关协变量的稀疏集。基于此,对2012年欧洲杯和2014年FIFA世界杯的赛事进行了预测。这些方法表明,当涉及到许多协变量和/或单变量的预测能力事先不明确时,正则化估计方法可能是有益的。
许多研究人员已经放宽了对条件独立性的强烈假设,并且引入了不同的可能性来将依赖分数考虑在内。Dixon和Coles(于1997年)首先确定了得分数之间的一个(轻微负)相关性。因此,他们引入了一个附加的依赖参数。然而,他们忽略了一个事实,即模型中的强度参数,包括两个团队的能力(或协变量)本身是相关的。因此,尽管以能力为条件,泊松分布被假定为独立的,但它们是边际相关的。Karlis和Ntzoufras(于2003年)提出用双变量泊松分布(bivariate Poisson distribution)对两个团队的得分进行建模,该分布能够解释得分之间的(正)相关性。尽管双变量泊松分布只能解释正相关性,但基于copula的模型也允许负相关性(可参见McHale和Scarf于2007年、McHale和Scarf于2011年或Boshnakov、Kharrat和McHale于2017年所提出的观点)。
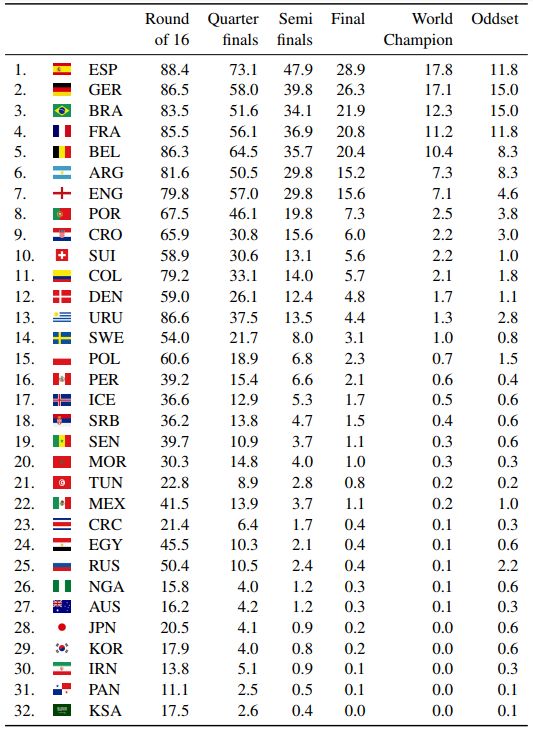
图3:根据FIFA世界杯的100,000次模拟运行以及根据ODDSET赔率获胜的概率,为所有32支球队进入2018年世界杯足球赛不同阶段的预测概率(以百分比表示)。
然而,关于双变量泊松的案例,Groll、Kneib、Mayr和Schauberger(于2018年)提供了一些证据,如果两个竞争团队的高信息量协变量都包含在两个(条件性)独立泊松分布的强度中,那么比赛分数的依赖结构可以被适当地建模。他们包括了欧洲杯数据的一大组协变量,并使用提升算法(boosting approach)来选择一个用于预测2016年欧洲杯的稀疏模型。由于双变量泊松分布的依赖性参数从未被提升算法更新过,所以有两个(条件性)独立泊松分布就足够了。
与基于协变量的泊松回归模型密切相关的是基于泊松的足球队伍排名方法。主要思想是找到能够反映当前团队最佳实力的足够多的能力参数。以一组比赛为基础,然后通过最大似然法(maximum likelihood)估计那些参数。Ley、Van de Wiele和Van Eetvelde(于2018年)研究了各种泊松模型,并对它们的预测性能进行了比较。由此产生的最佳模型是独立泊松模型以及Karlis和Ntzoufras(于2003年提出)的最简单的双变量泊松分布。有趣的是,Ley等人(于2018年)发现,这些模型在国内联赛和国家队比赛中的表现都优于对手。这些基于统计力量的排名为国际足联的排名提供了一个有趣的选择。





