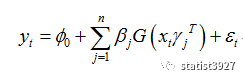因工作的需要,最近用到一个比较新的回归和预测算法:神经网络非线性自回归。我相信很多人乍一看着个算法的名字,都会有一种
“
水煮宫保鸡丁盖浇饭
”
的感觉。这个算法的组合怎么这么矛盾和混乱啊?
神经网络算法,但凡了解过机器学习的人都知道,是一种可以用在非线性回归(也有人爱用
“
非线性仿真
”
这种叫法)上的一种算法,其算法核心可以是
“
线性
”
的,以
BP
算法为例;也可以是非线性的,例如多层卷积算法。理论上前人早已能证明,
2
层以上的神经网络模型可以无限逼近任意的非线性曲线。
自回归,那就是更加以线性模型为代表的算法了。大家如果学过时间序列,一定学过
ARIMA
模型,这个模型中的自回归
AR
部分,就是一个典型的线性模型。
ARIMA
模型主要用来计算平稳的时间序列。
既然这个算法组合中的
2
个主要算法,都可以是线性的,为啥又非得在算法名字中加一个
“
非线性
”
三个字呢?
于是我真的研究了这个算法的
R
语言的算法包说明,并顺着作者所列举的首要参考文献《
Non-linear time series models in empirical finance
》做了认真的研读,发现里面的学问还真的大了咧。
如果说用什么自然科学的理论来做个比喻或者借鉴的话,我觉着这种
“
水煮宫保鸡丁盖浇饭
”
算法,还真的有点像傅里叶变换。或者说要去了解一个未知的曲线,是可以用若干个已知曲线去无限逼近的。
由简到难,举个例子来描绘下傅里叶变换
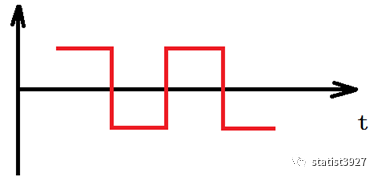
上面这个图是一个连续的信号图(或者你可以任意想象一个不规则曲线),如果想用一个线性的函数
f(t)
来表示的话,会很难甚至不可能。所以说上图是非线性的。
但是如果用大量的离散的正弦波来不断的逼近并线性叠加的话,则是可以无限的去模拟出这个非线性曲线的。

变成
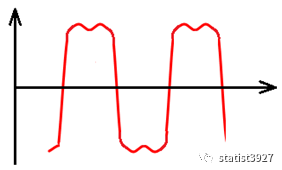
有了上面的变换例子,下面再来介绍这个算法,就相对容易些了。
在真实的财经领域,很多指标的历史序列图都是非线性的,同样一个指标有些甚至还存在一定的时间和空间上的差异。
我们平常用于分析的数据,一般例如销售数据,都是以月为频率进行分析的。但是像股票金融市场,甚至是电商的数据、
BAT
的平台数据,可能就是以小时为频率的。当然了,根据不同的需要,也有将这些高频的数据
“
降频
”
到月、季进行分析。
某一些场景下,一个数据的时间序列或呈现出不同的区制现象(
regime
)。有些学者喜欢用状态一词。
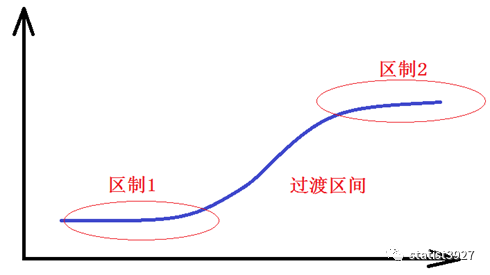
例如下图
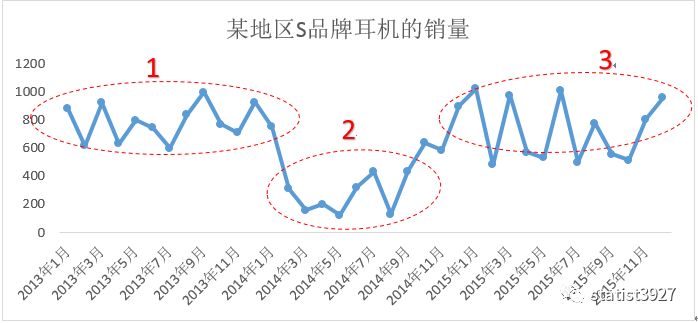
那么对于这种现象,我们明显的就可以看出,不同区制下的数据背后肯定有不同的影响背景,或不同的影响主因在起作用。
对于区制
1
和区制
2
,区制
2
和区制
3
,明显就是有一定的跃迁。其中区制
1
和区制
2
之间变化的比较剧烈,仿佛存在一个门限;而区制
2
和区制
3
变化的过渡就比较缓慢。
那么问题来了,如果让你用一个自回归时间序列模型来做拟合或者做预测,该如何做呢?
说实话,这就是一个不可能的任务。
因为时间序列的自回归算法,本身就是一个线性算法。换句话说,想要用自回归,整个序列就必须是平稳的,是不能出现这种区制的现象的。
当然了,你可能会说,有区制怕啥,我做一阶差分不就行了嘛,或者最多
2
阶差分。
哎,兄弟,其实你可能没理解做差分的现实意义:那是为了消除趋势!而区制的存在,会造成差分后依然不平稳
不信的话,如下图一阶差分的效果
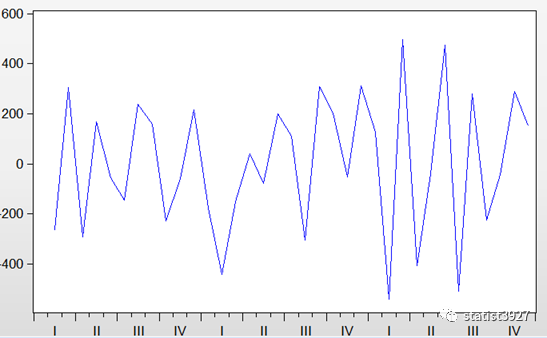
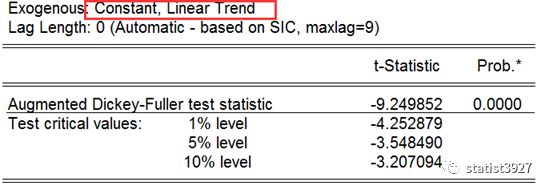
然后我们用
ADF
方法测算一下它的平稳性,我们检测下差分以后,不带趋势、带趋势、带趋势和截距项三种场景的平稳性,结果发现
NG!
其实,有经验的人很容易看出,为什么差分后仍然不具备平稳性,就是差分后的曲线的振幅,呈现出一种震荡变大的趋势。
嘿嘿嘿
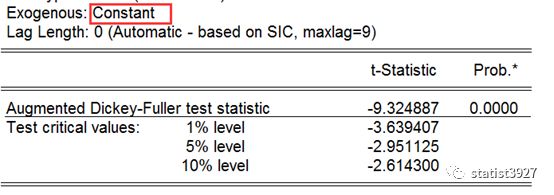
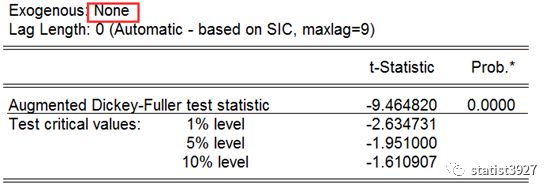
那么,既然直接用自回归用不成了,或者说线性的方法用不成了,那该如何解决这个问题呢?
这个时候,就要用到这种用已知的线性的方法来逼近非线性的
“
水煮宫保鸡丁盖浇饭
”
算法了。
这种方法的原理是这样理解
:
首先,不同的区制内的序列,是相对平稳的时间序列,可以用自回归模型进行建模的;
其次,不同区制间的过渡,无论是较为突然的跳变还是较为平稳的过渡,都是可以用一个门限函数进行表征,例如
logistics
函数。
最后,多个离散的自回归
+
门限模型的组合,只要调整好他们的系数,就可以无限的逼近一个包含多个区制在内的时间序列。
该序列的最核心算法如下:

上面的算法,如果大家还记得矩阵代数的话,就可以看出

中的

其实就是一个自回归模型
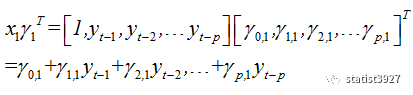
只不过这个自回归模型被当成了
logistics
方程的自变量而已。
而
G(.)
本身则构成了
2
个区制之间的衔接骨架,为什么这么说呢?我们可以先回忆一下
logistics
方程的曲线长啥样
我们看到,上图的蓝色曲线就是
logistics
方程,实际的值域里,如果不给它加一些额外的系数的话,它的值域∈(
0, 1
)。而一旦加入其他系数的话,它其实就可以构建出任意
2
个区制的曲线骨架。而且过渡区间的陡峭程度也根据系数的不同而不同。
上面这个核心算法,就构成了一种
2
区制下的曲线的回归。而多个区制的曲线纵向叠加的时候,那么它们就可以逼近复杂的非线性序列,于是上面的算法就转变成了这样

写到这里你可能头脑里有个疑问,为什么多个
logistics
曲线叠加就可以无限逼近一个复杂的非线性曲线呢?
那好我们还是按照《
Non-lineartime series models in empirical finance
》中举的简单例子来说明下。
下图蓝色的比较粗的曲线,就是我们想要无限逼近的一条非线性曲线;
绿色、紫色、橙色的线则是三条不同的
logistics
自回归方程
G(.)
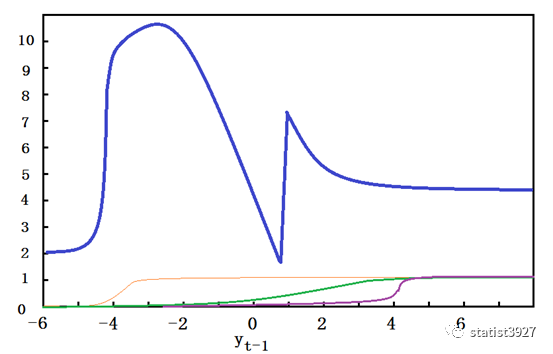
为了简单说明,
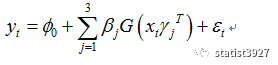
方程中的
x
t
仅表示
[1
,
y
t-1
]
T
。
我们令
φ
0=2
,因为只有
3
条用于演示的
logistics
方程,所以
D=3
;
再令
β
1
=9
,
β
2
=-11
,
β
3
=6,
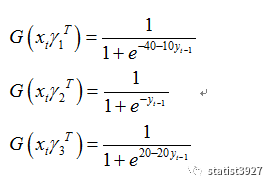
当
y
t-1
取较大的负数的时候,所有的
G(.)
线都接近于
0
;此时根据
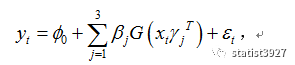
所有曲线叠加之后,等于
φ
0
,也就是
2
;
当
y
t-1
=-4
附近的时候,橙色的线条开始迅速增长并接近于
1
,而其他绿色、紫色的线条也还很小,于是整个方程实际上就是相当于
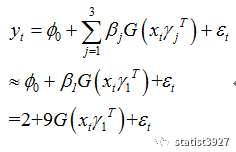
这也就是上图中蓝色线条陡然增大的原因。
如此类推,当
y
t-1
取值从
0
到
4
时,绿色的线条开始增长并接近于
1
,此时紫色线条还很小,于是整个方程实际上就相当于
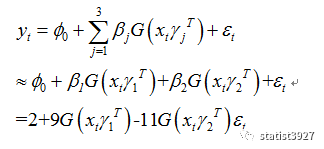
这也就是上图蓝色线条又迅速下降的原因。
继续,当
y
t-1
取值
4
及以上的数值时,紫色曲线开始激活,并迅速增长到
1
,此时所有的曲线方程实际上就变成
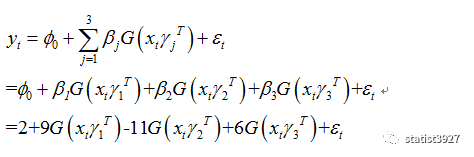
这样就最终实现了蓝色曲线的第三阶段:先陡增然后又平缓下降。
啊,原来是这样啊!
这就是如何用已知的有限的线性序列来逼近一条非线性的序列。
搞清楚了这个问题之后,那么新的问题来了。
这个算法的名字叫做
“
神经网络非线性自回归
”
,那神经网络又是如何和它们扯上关系的呢?
其实,这只是一个巧妙的“暴力求解”的表现形式。
我们回忆下,如果要估计出一条回归方程的系数,我们需要用到
OLS
方法。但是现在我们的目的不再是估计系数了,而是不断的用不同的系数带入到这个