第一次接触线性代数是在大一第一学期，学完后分数不低，但是结束考试过完俩周的我就产生了心虚，我觉得自己仿佛没有学到什么东西，记忆中只有那零零碎碎的计算公式.真正慢慢理解是大二开始参加数模比赛，重新学习了一遍对线性代数的实质稍微有了一点基础，直到后面接触硕士课程和一些算法查找很多网络上的资源，才慢慢的让我对线代的理解更加加深.下面的行文思路是我在网上找到的一个非常好的基础视频的总结笔记，期间会穿插着自己的理解.一来可以帮助像我一样的同学了解一些线代计算后面的本质，二来也可以帮助自己复习总结.
前方高能！这里我不会谈论一些计算性的东西，比如关于解的存在性、唯一性都有理论上的判别依据，要具体地求解的话又有Cramer法则，最不济我们拿个MATLAB这种数学软件都能解决，我更想总结的是一些计算背后的本质~由于比较基础，大牛请绕道~哈哈~开写！
-向量
线性代数最基础，最根源的组成部分就是向量，向量的线性组合构成了线性代数的基本运算.我们首先来介绍向量.
直观上，向量通常被标示为一个带箭头的线段。线段的长度可以表示向量的大小，而向量的方向也就是箭头所指的方向。-维基百科
从上面维基百科的定义中，我们可以得到决定一个向量的是它的长度和它所指的方向共同决定，只要保持这俩个量（方向和长度）不变，那么你可以随意移动向量而使它不变.
实际上，向量在科学中的表示，通用的有三种表示，第一种用带有箭头的线段表示，一种用符号吧表示，一种用有序数组表示，它们看似不同，实际上只是向量的不同描述~如下图：
那么问题来了.先上图：
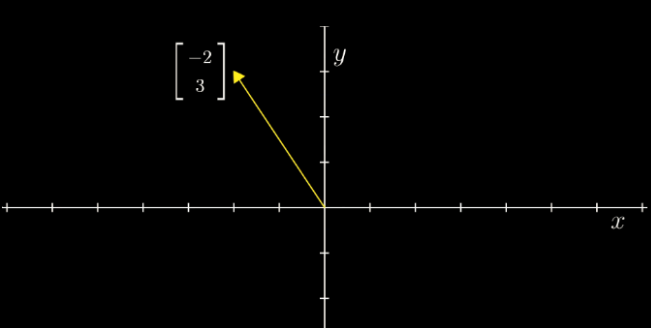
上面说了向量是可以随意走动的，只要方向和长度不变即可，那么如何确定是如何与图上向量一一对应呢.
答：在线性代数中，向量的起点往往是以原点开始，那么每一个有序数组都能在坐标系中唯一表示一个向量.
总而言之，向量就是一个从原点出发的箭头，有着方向和大小.可以用有序数组表示.并且由于默认起点是原点，一个有序数组唯一代表了一个向量
-空间
首先我们来看一下与的线性组合表示为：
那么下面我们给出空间的定义：
所有表示为给定向量线性组合的向量的集合被称为给定向量张成的空间.我们来考虑俩种情况，当与共线与不共线俩种情况，它们所张成空间的情况.
-当与不共线的时候,大部分情况还是这样，它们线性组合构成的向量集合是什么？
它们随着俩个向量前面系数的改变，它们张成的空间是所有二维向量的集合（也就是整个二维空间都会被充满）.下面我们来解释一下.
当向量前面系数不变，前面系数在实数范围内改变的时候，我们可以得到平行于向量的所有二维向量.如下图：
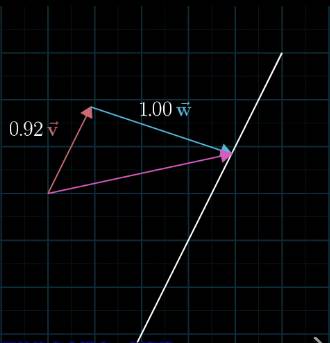
它们组合的向量终点是在白线上（后续会说明为什么向量还可以用一个点表示，其实也容易理解，起点默认了是原点了）.
那么我们可以这样理解，对于每一个前面系数在实数范围内变化，我们可以看成这条白线往方向来回平移，这样二维平面内的向量都能被充满.这样也就解释了为什么俩个不共线的向量能够线性组合为所有的二维向量.也就是说，当俩个向量不共线的时候，它们张成的空间是整个二维空间
-当与共线的时候,它们线性组合构成的向量集合（也就是张成的空间是什么）是什么？
当俩个初始向量共线的时候，所产生的向量的终点被限制在一条过原点的直线上.
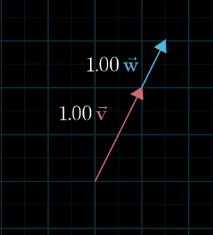
这非常好理解，可以把这俩个向量旋转到轴，平行的俩个向量，无论你怎么线性组合，组合出新的向量都是在轴上.当俩个向量共线的时候，它们所张成的空间是平行于
向量的一维直线.
下面我们来考虑三维的情况.先上图
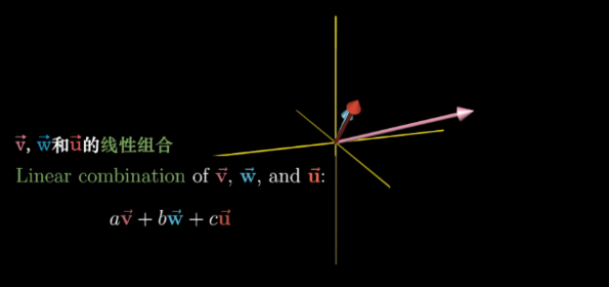
很显然，我们类比也能得出，当三个向量不共面的时候，它们张成的空间是整个三维空间，当三个向量不共线但是共面的时候，张成的空间是它们形成的二维平面，当他们共线的时候，那么张成的空间就是那条直线.下面我解释一下为什么这样，以及能够更好的推广到高维空间.
-三个向量不共面的时候
我们可以首先看在三维空间中俩个向量不共线的情况如下:
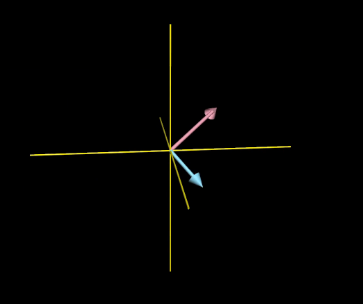
根据我们前面的分析，我们很容易得到，这俩个向量张成的空间是三维空间中的一个平面，如下图：
那么当第三个向量如果在前俩个向量张成的空间内，那么这三个向量张成的空间就是这个平面
当第三个向量不在前俩个向量张成的空间内，那么它们三个向量张成的空间是整个三维空间.这又如何思考呢？
当前俩个向量张成一个空间的时候，第三个向量（下图是红色向量表示）控制了最后张成的空间，可以这里理解：当你缩放第三个向量时，它将前俩个向量张成的平面沿它的方向来回移动，从而扫过整个空间.over！这就解释了它们三个向量张成的空间是整个三维空间，下图显示：
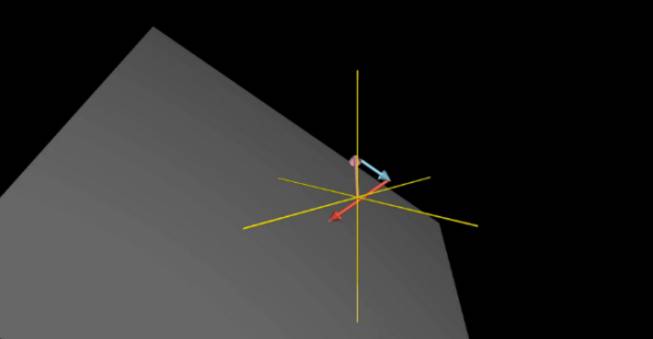
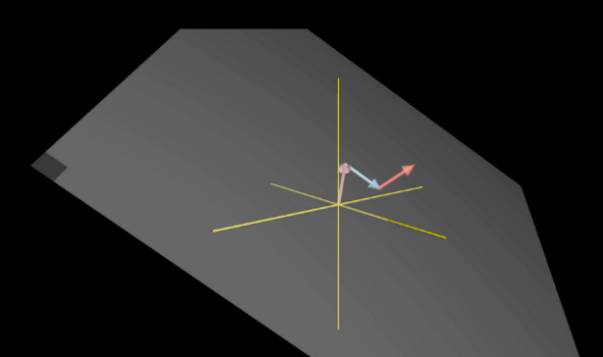
当第三个向量（红色向量).上下移动的时候，前俩个向量构成的空间沿着这个向量方向移动，从而扫过整个空间.最后解释一下三个向量共线的情况，张成的空间就是那条直线上的一维空间.由于我们生活在三维空间中，四维以上的空间我们无法想象到，可以通过类比上去，这也是线性代数的一个很重要的思想.
-为什么有时候向量可以用点来表示
想象落在一条直线上的一些向量的时候，你会觉得比较拥挤
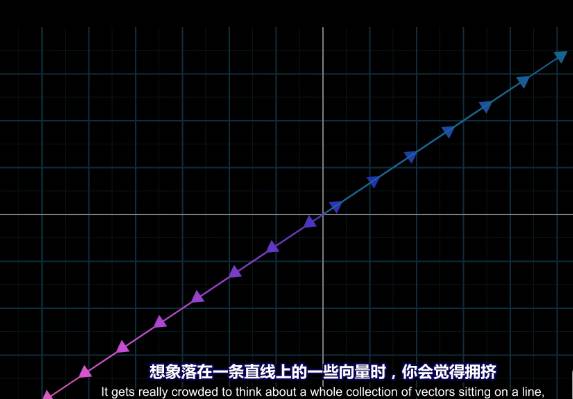
同理想象所有二维向量填满平面时，你会觉得非常拥挤
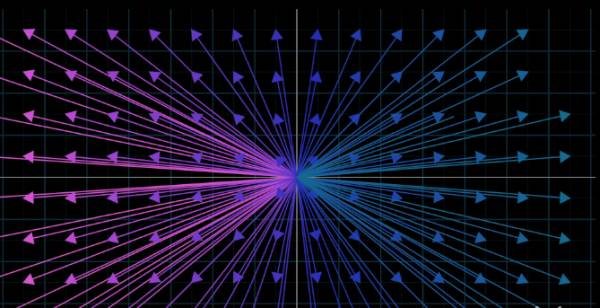
所以为了对付这种情况，通常我们就用向量的终点来代表该向量，如下图：
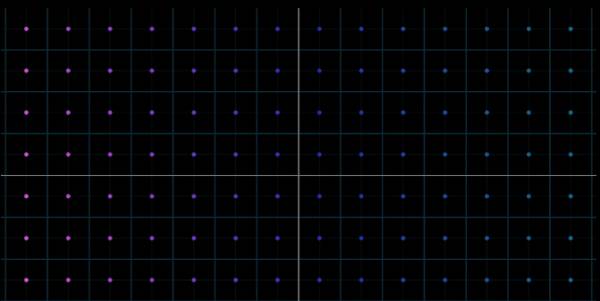
这也就解释了为什么向量有时可以用点来表示~
鉴于每篇文章内容不宜过长，后续的线性相关，矩阵乘法，空间变换，特征值与特征向量等知识会后续连载几篇文章.今天是除夕，祝大家新年快乐，新的一年新气息！哈哈哈哈哈~
下面给出我认为非常好的资料推荐：
1【双字/合集】“线性代数的本质”系列合集(3)
https://www.bilibili.com/video/av6731067/index_3.html
非常非常好的视频，制作者良心巨作啊！（上述图片均来自此视频~）
2 线性代数的几何意义pdf.(我买的是纸质书，电子书我找了很久，只有部分，想要完整的还是要买纸质版.pdf分享在百度网盘链接：http://pan.baidu.com/s/1i4AQ9N3 密码：17x1)
3 MIT线性代数课程视频 （分享链接：http://pan.baidu.com/s/1jI2rrYu 密码：fl72）
4 线性代数的本质--对线性空间、向量和矩阵的直觉描述 - tenos - 博客园
http://www.cnblogs.com/TenosDoIt/p/3214096.html
（这个理解矩阵连载是我见过最能体现线性代数本质的文章）
希望大家一起学习，一起进步，新年快乐~
往期经典文章回顾
高等数学、线性代数、概率论与数理统计、几何学这些知识可以用来干什么？主要应用有哪些？
线性代数的本质--对线性空间、向量和矩阵的直觉描述
理解矩阵背后的现实意义
数学系和物理系学生有什么差别？
线性代数的本质
Leibniz 如何想出微积分？（三）
PCA的数学原理
零除以零在数学中有意义吗？
算法|人人都该了解的十大算法
对傅里叶级数的理解
