作者:汪璐 (中国科学院高能物理研究所)
1.1 深度学习的基本原理
深度学习是一种通过多层叠加的非线性处理层构成的计算网络,如图1(a)所示。输入层x 与输出层y 之间包含了多个隐藏层,每个隐藏层节点是一个非线性函数,该函数的输入z 是前层输出的一个线性加权,权重是wij(从上层第i 个输出到本层第j 个处理单元的权重)。这类网络理论上能够拟合从输入向量到输出向量的任意函数。对于分类问题,这个函数可能是一个输入x 属于某个输出类别的概率;对于预测问题,这个函数可能是从x 到y 的复杂变换的一个拟合。如果通过某种逻辑组合使用多个深度学习网络,还能够实现降维、去噪、还原、模拟生成等复杂计算。
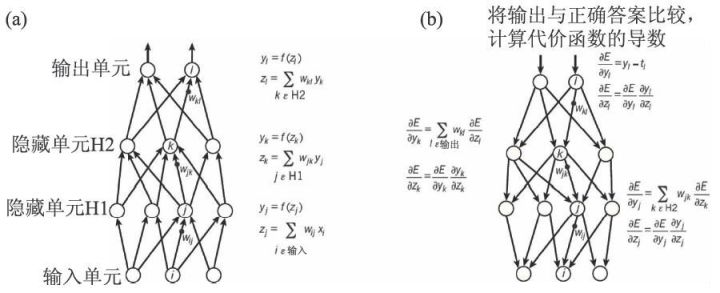
图1 深度学习的基本思想
“学习”指的是通过梯度下降求解wij 的过程。“学习”开始前,算法会对所有的wij做随机初始化。此时,随机抽样一批数据样本代入,模型输出与预期输出之间会存在差距E,它是一个输入向量的复合函数,参数是所有的wij。根据微分的链式求导法则,我们可以求出E 对最后一层参数的偏导,并且把偏导向量逐层传递给网络的所有权重,求出所有∂E/ ∂wij,如图1(b)所示。∂E/∂wij定义了函数E 的梯度方向,沿着这个方向调整wij可以使E最快速地收敛到最小值。从模型输入到输出的计算叫做Feed Forward(前馈)过程,微分反向传递的过程叫做Back Propagation(反向传播)过程。假设所有样本独立同分布,每执行一次“抽样前馈—反向传播—参数调整”,可以使wij离合理的配置更接近一些。当E 足够小时,可以认为算法学习到了wij的最优解,“学习”结束。
这种思想在上世纪80 年代就已经被提出,由于其计算过程与神经系统的一些相似性而被取名为神经网络。与支持向量机、提升决策树等同期出现的算法比较,神经网络在学习参数时需要大量的计算资源和训练样本,又存在训练复杂、结果泛化性能差等缺点,在上世纪90 年代到本世纪初的十几年内曾一度消迹。2006 年后,随着计算能力的提高、训练样本的扩大以及训练方法的改进,该算法逐步在人工智能领域取得突破,成为该领域最主流的算法,从实践上证明了该计算方法的合理性。现在,谷歌、微软等大公司训练的深度学习网络动辄包括上百个处理层、数十亿个权重参数。由于从输入到输出要经过很多层的变换,所以该算法形象地有了一个新的名称——“深度学习”。
深度学习以外的机器学习算法在遇到图片、音频等高维复杂的原始数据时,会表现出建模能力的局限性。例如,图片分类任务中,同一个位置的一只白狼和一只萨摩耶的原始图片输入非常相似,但我们要求给出不一样的输出。不同位置的同一只猫的原始输入非常不同,我们要求给出相同的输出。解决这类问题,首先需要领域专家基于经验从原始数据中提取适于解决某个问题的抽象特征。基于这些抽象特征,才能使用传统机器学习算法进行分类预测。深度学习强大的建模能力使得它能够从数据中自动学习到这些分类特征,大大降低了开发难度。同时,当数据足够多的时候,模型学习到的特征比人工设计的特征更优,因此算法的预测性能更好。这两点决定了深度学习算法较其他机器学习算法具有压倒性的优势。
1.2 高能物理学家为什么对深度学习感兴趣?
上世纪90 年代,高能物理学家就曾使用神经网络来处理实验数据。2014 年,深度学习在高能物理领域卷土重来。截至目前,与深度学习相关的会议就有7 个,arXiv.org 上近三年来相关的文章已经有上百篇。高能物理学家对深度学习算法的热衷并非一时兴起,主要有如下考虑。
(1) 高能物理主要的研究手段是对海量数据进行统计分析,领域内已经有很多传统机器学习算法的应用,例如粒子鉴别、事例分类、异常检测、粒子径迹的模式识别等。
(2) 深度学习是一类需要大量训练数据样本的算法,高能物理领域数据资源非常丰富。
(3) 如果将深度学习模型看成一个通用函数模拟器,那么复杂的算法都可以用它来替代。有些场合下,深度学习的预测性能甚至优于人工精心设计的算法,使用深度学习是性能和成本的双赢。
(4) 并行化是高能物理计算的大势所趋。深度学习算法天然地支持并行计算,而很多实验在传统算法的并行化问题上还在消耗着大量的人力财力。
(5) 训练完成后,深度学习的推理(Inference)计算比传统的算法要简单得多。一次训练多次调用,可以节约计算资源。
(6) 人工智能时代,各公司争夺的主要目标是数据和用户,对技术的分享特别慷慨。谷歌、微软、百度等大公司开源了近10 个的深度学习软件框架,这些框架中又包含大量的算法实现、训练数据集甚至训练好的模型参数。技术的民主化大大降低了基于深度学习的应用的开发难度,物理学家可以节约出更多的人力进行本领域的研究。
按照网络结构和应用场景的差异,深度学习可以细分出深度神经网络、卷积神经网络、递归神经网络等计算模型。按照训练样本中是否包含预期结果的标注,深度学习可以划分为监督学习和非监督学习。下文将以此为参照,介绍深度学习在高能物理领域的应用。
2.1 基于深度神经网络的分类
深度神经网络(Deep Neural Networks,DNN)是一种最简单的深度学习模型。与图1 中的结构一样,每个隐藏层单元的输入是前一层所有输出的线性加权。“深度”主要体现在比传统神经网络更多的隐藏层数。
2014 年Baldi 等人基于DNN实现了超出标准模型的新物理信号和本底判选。在寻找超出标准模型的新物理中的额外重希格斯玻色子的问题中,他们生成了约一千一百万的模拟样本,其中包含新物理中的额外重希格斯波色子信号(gg->H->WH->WWh->WWbb)的样本和标准模型背景样本(qq->tt->WWbb)。
分类的输入特征共28 维,包括横动量、Jet参数等21 个底层变量以及Axial MET、Sum PT等7 个高层变量。通过对网络深度、隐藏层单元数、学习率、权重衰减等超级参数的调优配置,作者在一个DNN网络(5 个隐藏层,每层300 个计算单元)上实现了8% 的分类效率改进(与提升决策树算法比较)。这项工作同时验证了深度学习的特征学习能力:只使用21 维底层特征和同时使用28维输入特征的分类效果几乎一样,这证明了物理学家精心设计的7 个高层分类特征已经被DNN网络学习到了。
2014 年,ATLAS实验还将一个类似的数据集放到机器学习竞赛平台Kaggle 上,以奖金激励的形式寻求该问题的解决方案。最终,一个基于DNN集合(平均多个DNN网络输出)的方案获得了分类精度这一性能指标上的冠军。
DNN的连接方式决定了它很难将网络做到很深,也很难处理图片、音频等特别高维的原始数据。假设输入是一个30 万维的向量(100 kB 的图片),每个隐藏层有10 万个隐藏单元,每增加一层就会增加300 亿个参数。反之,如果输入特征维数较低,并且有足够的训练样本,DNN的分类和预测效果一般会优于其他的机器学习算法。
2.2 基于卷积神经网络的分类和预测
2.2.1 卷积神经网络
卷积神经网络(Convolutional Neural Networks,CNN)是计算机视觉领域最经典的深度学习算法,特别擅长处理图像、视频等高维的能够组织在一个2D 平面上的输入数据。模型包括卷积、线性整流、池化和全连接等计算过程。
(1)卷积(Convolution)
卷积操作通过一个小型的卷积核依次与图片中相同大小的区域做点乘,对图片作线性变换,如图2 所示。无论输入图片有几个信道,与一个卷积核卷积后,都只剩下一个信道。该信道中的每个像素的数值是多个信道卷积结果的叠加。卷积操作大大降低了每层变换需要的参数个数:参数个数取决于卷积核的大小和个数,与图片的大小和深度无关。如果一个卷积层使用了16×3 个5×5的卷积核将一幅3×1000×1000(3 K)的彩色图片变成了一个16×1000×1000 的张量(注:假设卷积时,使用边缘填充,保持图片的长宽不变),那么这个卷积层包含的参数约为16×3×5×5=1200 个,而在DNN网络中,这个变换需要约4800 万个参数。这个操作是符合我们的一些先验知识的:图片中对预测有帮助的特征信号只存在于某个局部区域,同时该信号具体在哪个局部区域不影响预测结果。
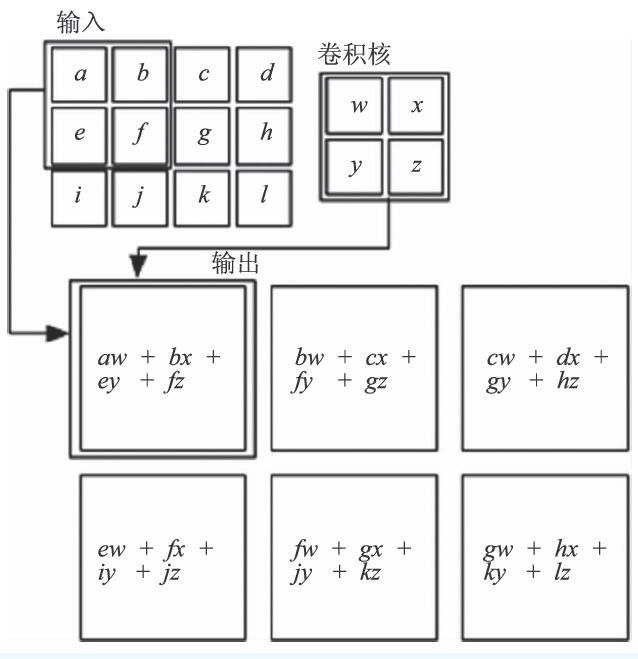
图2 用一个2×2 卷积核对一张4×3 图片做卷积的过程
(2) 线性整流(Rectified Linear Unit, ReLU)
卷积是一个线性变换,每次卷积后需要对结果做一次非线性变换。目前,深度学习中最常用的非线性函数是线性整流函数(Rectified Linear Unit,ReLU)。ReLU(x)=max(x,0),这个函数计算起来非常简单,也不会出现梯度消失等问题,是深度学习模型能够变深的重要保证。
(3) 池化(Pooling)
跟在ReLU 之后的池化(Pooling)操作将一个图片窗口内多个像素合并成一个像素,这样做不仅可以对信号降采样,缩小下层计算的输入尺寸,同时也可以减少局部数据扰动对结果的影响。
(4) 全连接层
经过多次地“卷积—ReLU—池化”,CNN模型逐步将原始数据转换为局部的特征信号,底层的特征信号组合成高层的特征信号,高层的特征信号变换成抽象特征信号,如图3所示。因此,在CNN模型的尾部,只需一个浅层(比如3 层)的神经网络就可以完成预测任务。由于该网络中相邻两层节点之间是全连接的,这些处理层被叫做全连接层。
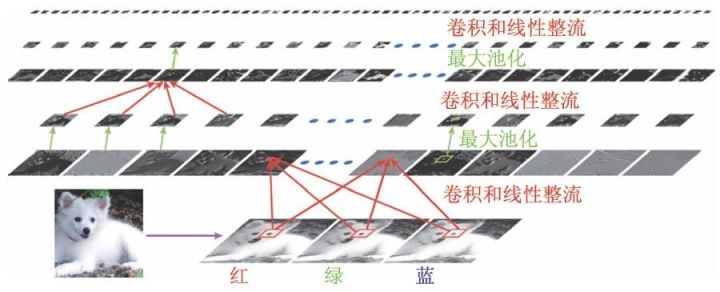
图3 卷积神经网络图片中提取特征的过程
如果我们将探测器看成一个照相机,将探测器单元的读出理解为图片的像素值,那么探测器的读出就变成了一幅幅“物理照片”。把这些照片作为输入,我们可以将物理上的分类、拟合问题转换为计算机视觉上的图片分类、物体定位等问题来解决。
2.2.2 Jet分类
Jet(粒子喷注)是指高能夸克或胶子强子经过部分子灼射和强子化形成的朝某个方向集中的大量强子。由于“色禁闭”,夸克和胶子无法单独存在,只能通过其强子化的产物观测,所以粒子物理实验需要重建Jet 来得到原初夸克或胶子的信息。Jet 的测量对高能物理实验研究至关重要。这其中的工作既包括Jet 来源的分类,也包括Jet 子结构的研究。
Jet 识别的传统方法是用径迹参数和次级顶点等信息进行判选或者多变量分析。近年来,物理学家提出基于Jet 图像的新预测方法。该方法通过以下步骤为每个Jet 生成一张“照片”:首先将探测器单元按照(η, ϕ )角度排布到二维图片上,图片的像素值是每个探测器单元的读出。然后通过角度变换、旋转,像素调整和翻转等预处理,使Jet 信号尽可能地处于图片的中心, 子Jet 尽可能处于图片正下方,右边的像素值总和高于左边,减少由于时空对称性产生的图片差异。通过这些照片能够直观地区别不同类型的Jet。图4 显示了多张图片叠加后W玻色子Jet ((a)和(b))和背景QCD Jet ((c)和(d))的对应图片的差异。由于前者存在子Jet 结构,因此在旋转前(a),中心Jet 信号周围有一个光圈。在旋转后(b),中心Jet信号下面有一个明显的像素聚集区,而后者在Jet 中心以外的像素分布则相对比较均匀。以这些照片为训练样本,可以训练一个用于Jet 分类的卷积神经网络。图5 显示了该方法相对于其他Jet分类方法的分类效率改进:(1)Maxout这一特殊的卷积神经网络性能最好;(2)普通的卷积神经网络性能其次;(3)图片归一化以后,普通神经网络的分类性能比不归一化更好。

图4 W玻色子Jet(上图)和QCD Jet(下图)的图片差异
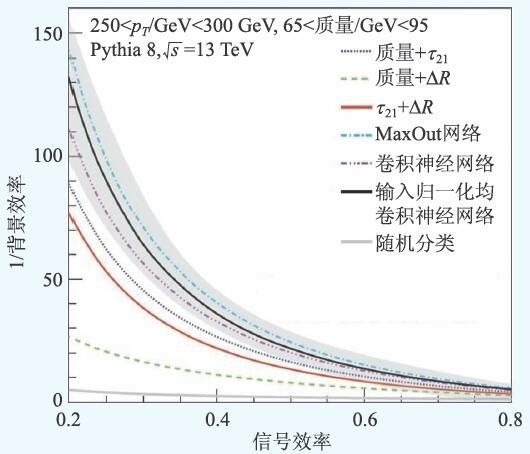
图5 Jet 分类问题上卷积神经网络较传统分类方法的性能改进
在处理夸克Jet 和胶子Jet 分类问题时,文献提出将量能器输出划分成带电粒子横动量、中性粒子横动量和带电粒子多重数三个信号通道输入给卷积神经网络的设计,模拟结果显示分类效率能够继续提高10%—20%。基于卷积神经网络的Jet 分类是一个活跃的研究领域,类似的工作还有文献等。
2.2.3 江门中微子实验的宇宙线缪子重建
江门中微子实验(The Jiangmen Underground Neutrino Observatory,JUNO)是一个测量“中微子质量顺序”的前沿实验,预计2020 年开始取数。实验的探测器主体是一个直径约35 m、蓄有2 万吨的液体闪烁体的球型有机玻璃罐。该有机玻璃罐被浸泡在一个水池内, 周围密布了约18000 只20 英吋光电倍增管(Photomultiplier Tube,PMT)。液体闪烁体是探测中微子的介质,当粒子穿过探测器时,会在探测器内发生反应,发出极微弱的闪烁光。这些光子在飞行的过程中会发生折射、反射、吸收等物理过程,最终被PMT探测到。利用PMT记录的电荷和时间信息,实验可以重建出物理事例。
宇宙线缪子是JUNO 实验重要的本底来源,它与探测器液闪发生反应会产生类似于中微子穿过的信号。每天穿过探测器的中微子大约只有60个,而平均每秒钟经过探测器的宇宙线缪子就有3 个。为了提高中微子探测的效率,我们希望重建出每条宇宙线缪子的入射点和角度,然后在一定时间窗口内拒绝(Veto)这条径迹周围一定体积内的PMT信号。传统的宇宙线缪子重建方法基于探测器的光学模型来预测缪子的入射位置和方向,受到折射和反射等因素的影响,重建结果并不理想。
2016 年,我们在小范围(7 万个随机分布模拟事例样本)模拟数据集上,验证了基于卷积神经网络的重建方法。我们将球面上的约18000 个PMT以0°经线为中心展开到一个二维平面图片。每个PMT 对应一个像素,相同纬度的PMT 排布到图片的同一行,图片的宽度=球面赤道上的PMT数量,其他部分填零,如图6 所示。然后用一个小型卷积神经网络(三层卷积+ReLU+池化,三层全连接)去训练预测模型。测试结果(基于1 万个测试样本)显示,该方法对径迹入射角和入射点位置的预测结果均优于人工设计的光学模型,平均误差分别是0.5°和9 cm,初步验证了该方法的可行性。
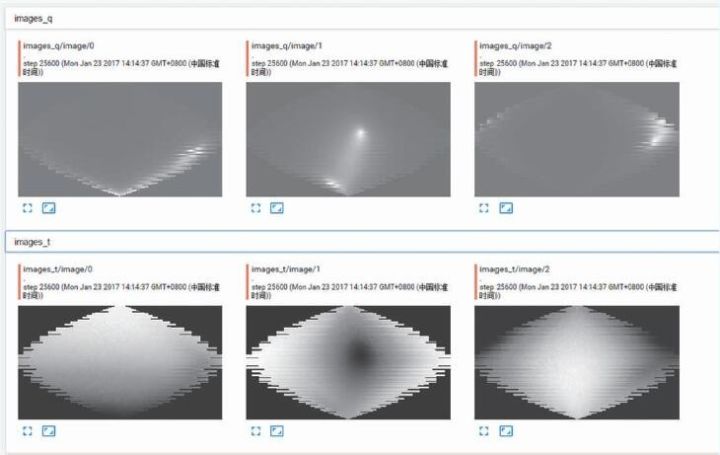
图6 宇宙线缪子在JUNO探测器上形成的“照片”(每一列代表一条径迹,第一行代表电荷Q,第二行代表时间T)
接下来我们将从以下几个方面对该方法进行改进:第一,在生成模拟数据时,增加对探测器构造细节(例如探测器部件对PMT的遮挡等)、时间的测量误差等因素的考虑,提高模拟数据与真实数据的相似性;第二,以零度经线为中心展开PMT 的方法会使有些径迹信号被人为的切割到图片的两边。我们将通过图片旋转和坐标变换来避免因此造成的信息丢失;第三,受到样本数量的限制,当前使用的模型是一个非常小型的卷积神经网络。接下来,我们将采用一些更深的模型和更大规模的数据样本来训练模型、验证结果。
2.3 基于递归神经网络的分类
递归神经网络(Recurrent Neural Networks,RNN)是一种擅长处理时序信息的预测模型。模型的输出不仅与当前时刻的输入有关,还与历史时刻的输出有关。现实生活中有很多这样的例子,例如在自然语言的理解中,一个词语的意思,通常与前面几个词语构成的语境相关。图7(a)描述了这样的一个原型概念,中间的方框是一个循环处理单元,每个时刻的输出Ht是当前输入Xt与上一个时刻的输出Ht-1 的函数,参数分别为Wxh 和Whh。如果我们将这个循环网络展开如图7(b)所示,可以发现这是一个与DNN相似的网络结构,如果能够求出最后一个时刻模型的输出与预期输出之间的误差E,就可以像训练DNN一样,通过梯度下降的方法求解模型参数Wxh和Whh。
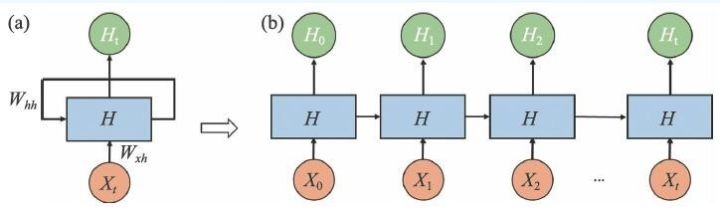
图7 递归神经网络及其展开
LSTM和GRU等递归神经网络对图7 中的结构做了改进,它们在循环处理单元中增加了多个非线性的门控函数,以建模时序输出之间长短不一、轻重不同的依赖关系。这些门控函数的参数也可以在训练过程中求解。
2.2 节中基于“物理照片”的分类方法,需要借助一个假设前提:探测器的所有探测单元大小相同且均匀分布。实际上,很多探测器是不满足这一假设的,因此,在进行图片预处理时会导致部分信息的丢失。Louppe 等人提出了基于递归神经网络的Jet分类方案。
假设每个Jet 包含多个粒子,该方案将每个粒子的四动量按照一定规则排序成一个二叉树。然后按照自底向上的顺序,将该二叉树输入一个递归神经网络,如图8 所示。每个循环单元的输入X 是二叉树中当前节点的四动量,输入H是当前节点的所有子节点的输出。循环到二叉树顶点时,该神经网络会输出一个当前Jet 的40 维特征表示。基于此40 维特征表示,该方案用了一个浅层的分类器实现了分类任务。
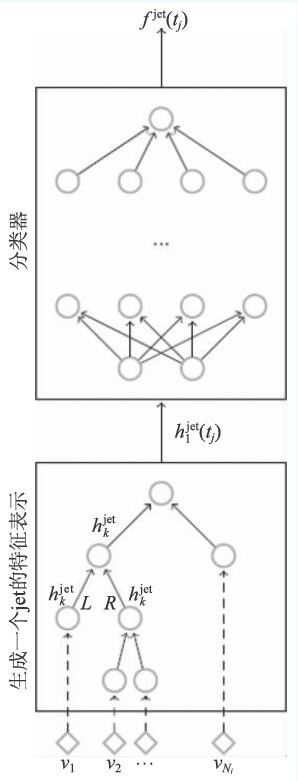
图8 基于递归神经网络的Jet 分类
相同数据集上的测试结果显示,这个方法比基于Jet 图片的分类方法在分类效率上提高了4%左右。同时,此方法使用的模型参数和训练样本仅仅为图片算法的10% 左右。Louppe 等人还将这个工作扩展到了事例分类上,如图9 所示。假设一个事例包含M个Jet,按照图8 的设计,能够得到M个Jet 特征向量和M个二叉树的顶点粒子的四动量。将所有Jet 按照二叉树顶点的粒子的四动量排序,然后把排序后的Jet 依次通过另外一个递归神经网络,则可以生成一个当前事例的特征表示。最后,模型基于事例的特征表示,用一个浅层的分类器实现了事例分类。
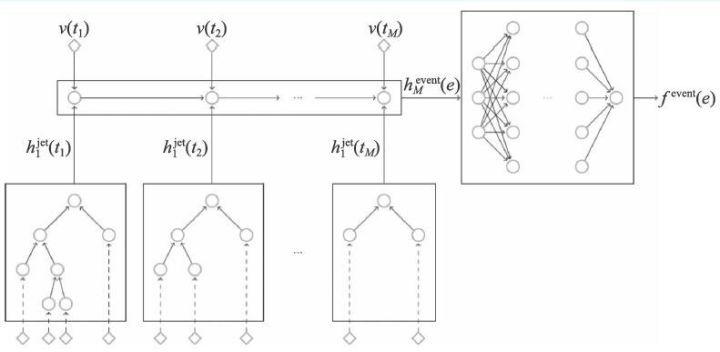
图9 基于递归神经网络的物理事例分类
2.4 基于非监督学习的应用
前文所述的模型都需要通过监督学习的方法进行训练,模型的预期输出是人工标注的,从时间和金钱上来说都是一笔昂贵的开销。同时,这和人脑的学习过程是不一样的:人学会辨识1000个动物并不需要学习上千万张图片。基于深度学习模型的非监督学习算法,例如自编码器AutoEncoder、对抗生成网络(Generative Adversarial Network,GAN)等,试图解决这部分问题。这些算法将深度学习网络当成一个复杂函数的模拟器,通过组合多个网络,能够从没有标签的数据中学习到解决问题需要的“知识”,表现出强大的学习能力。
2.4.1 自动编码器
如图10 所示,一个自编码器包括编码器和解码器两个部分,分别用神经网络进行建模。编码器将输入特征x 转换为隐藏特征z,解码器将隐藏特征z 重新转换为x。如果我们将这个模型训练的代价函数设置成||x2-x'2||,即要求x'和x 尽可能的相似的话, 模型学到的隐藏特征z 就是x 的一个非线性特征表示。
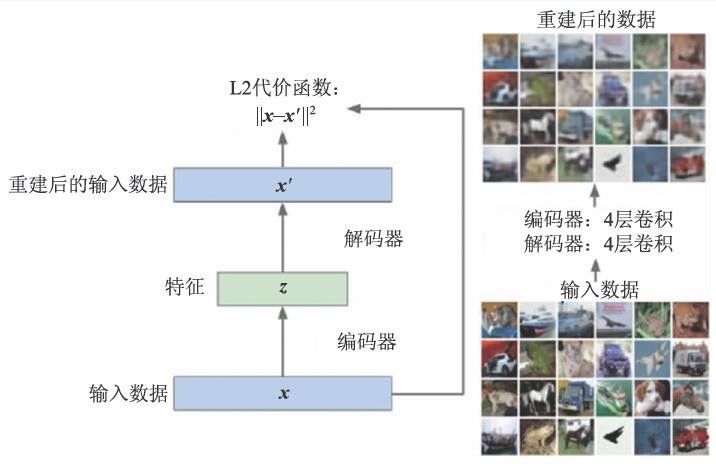
图10 通过自编码器学习输入数据x的核心特征
如果z 的维数远小于x 的话,我们就通过自动编码器对数据进行压缩和还原。如果我们用编码器的参数来初始化一个基于x 的分类模型,那么,用更少的标注样本就可以达到相同的训练效果。自动编码器还可用于预测结果的可视化。文献中将大亚湾探测器的“物理图片”用卷积自编码器进行了自编码,将自编码后的结果通过t-SNE算法呈现在了一张2 维图片上,结果表明,相同类别的粒子图片在这张照片上的位置更接近。
2.4.2 对抗生成网络
对抗生成网络算法能够训练一个样本生成器,该样本生成器在训练过程中隐式地学习到了训练样本的分布函数,因此它可以将随机的噪声信号,转换为与训练样本“非常相似”的模拟样本。如图11 所示,这个模型包括样本生成器和样本区分器两个网络。训练过程中,样本生成器尽量地通过调节参数,生成区分器无法辨别的样本。区分器则尽量地通过调节参数,发现生成器伪造的样本。通过这两个网络的迭代“互博”,样本生成器生成的样本会越来越逼近真实的样本。在计算机视觉上,对抗生成网络可以用于图片渲染、恶劣天气下的图片还原、图片去遮挡等应用。

图11 对抗生成网络示意
模拟计算消耗了整个高能物理计算资源的50%以上。文献两篇文章实现了基于对抗生成网络的探测器模拟策略。这两个工作也是基于探测器可以类比于电子照相机这一假设前提的。首先用模拟软件生成不同的粒子经过每层探测器的“物理照片”,之后以这些图片为训练样本,训练一个“物理照片”的生成器。如果生成器生成的图片可以无限逼近模拟软件的生成图片,就可以基于这些图片实现探测器的快速模拟。文献的工作中,图片生成器生成一个Shower 需要的计算量比传统算法降低了2 个数量级;如果在GPU上并发执行,生成一个Shower需要的时间可以降低5个数量级。
以上工作只是一些初步的尝试,基于GAN的快速模拟还需要考虑3D模拟、多层模拟等更复杂的探测器环境,以及提供一些可量化的性能指标。
深度学习算法以其相关的软件框架、硬件体系结构还处于快速发展的阶段。在现有高能物理计算环境中应用这一强有力的数据分析工具,还面临着以下的问题。
(1) 结果的可解释性和量化误差
深度学习的模型结构和训练方法与人脑的神经系统有一定的相似性,一些设计细节也借鉴了神经科学的研究成果。然而,当前只能从结果上证明其有效性,算法本身并没有完备的数学证明。高能物理是一门严谨的科学,深度学习模型得出的预测结果,需要用物理学家认可的方式来证明其合理性。高能物理分析的每个计算结果需要给出量化的统计误差和系统误差,而深度学习算法模型的系统误差较难估计。
(2) 数据格式转换
ROOT科学数据分析库是各大高能物理软件共用的数据分析库,高能物理数据大多数是按照ROOT格式存储的。目前,ROOT提供一个Python 工具库root_numpy,解决格式转换问题。这个工具可以将ROOT 格式存储的数据转换为numpy 格式,后者是很多深度学习软件框架在内存中的数据组织形式。目前,这种转换不支持流式读入,转换开始前必须先将整个文件读入内存。这种设计假设了一次训练需要的数据样本可以在计算节点的内存中全部放下,大大限制了应用的模型规模。在解决JUNO 宇宙线缪子重建问题时,我们采用了折中的办法:先用root_numpy将每个ROOT 文件转换成numpy 格式的磁盘文件,然后再批量流式地读入这些numpy 文件进行训练。这个方法不仅浪费了很多磁盘空间,而且模型输入向量的设计发生改变时,还需要重新转换,不够灵活。
(3) 跨领域合作和数据集开放
深度学习算法及其相关的软件框架、硬件体系结构还在快速发展的阶段。为了更早的应用到深度学习领域的研究成果,应该开展跨领域的技术合作。合作的基础是相关数据集的开放。本文中提到的希格斯粒子分类问题、Jet 分类问题相关的数据集已经可以在网络上下载。
深度学习是大数据时代最成功的机器学习算法。传统算法计算复杂度高、开发难度大、难于优化和并行是促使高能物理学家考虑深度学习算法的主要原因。丰富的数据资源和诸多现成的应用场景为该技术在高能物理领域的应用提供了必要条件。目前,该算法在粒子鉴别、Jet 分类等计算任务上已经有成熟的应用。在径迹重建和快速模拟等任务上有原型实现,但离实际应用还有一定的距离,值得高能物理学家与深度学习领域专家进行进一步的跨领域合作和探索。














