○
方程一：
史瓦西度规是真空爱因斯坦场方程的一个解。史瓦西度规是一个静态度规。关于度规的更多讨论可阅读
《什么是时空？》
。
首先，在史瓦西的解中，有个叫作
事件视界
（Event Horizon）
的东西。这是一个有去无回的边界，一旦越过就再也无法以低于光的速度回来。如果你还记得史瓦西的解的形式
（见方程一）
，就会发现当 r = 2M
（r 为半径，M 为质量）
时出现的奇异性。尤其是度规的时间部分会消失，我们现在称之为
延时函数
（Lapse function）
。那就是事件视界所在。当半径变为零时
（r = 0)
，史瓦西的解中也具有奇异性，我们对其最好的理解是，这些奇异性标记着时空中真正的物理奇点
（r = 2M的奇异性可以通过坐标变换予以消除）
，几何自身在奇点处失效。如果你进入一个史瓦西黑洞，你就会遇到这个奇点，但我们不知道接下来会发生什么，甚至说不确定“接下来”是否是个恰当的词。
○
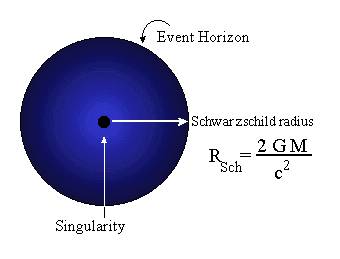
图一：
事件视界被认为是有去无回的点，它所包围的球体半径被称为史瓦西半径（Schwarzchild radius）。公式中G是万有引力常数，c是光速，M是质量。如果把太阳的质量代入公式就会得到史瓦西半径为3公里。
|
图片来源：Sunshine Lighthouse
我们多希望您可以看到在您离开20年后广义相对论的进展。其中约翰·惠勒
（
John Wheeler）
曾是这些成就的核心。
（而且我们真的认识他！他的生命延续到2008年，我们曾在普林斯顿一起度过许多时光。）
他普及了“
黑洞
”这个用来描述史瓦西的解和相关度规的概念。一位叫罗伊·克尔
（Roy Kerr）
的新西兰人找到了一个能用来描述旋转黑洞的更广义的史瓦西度规。这是一个比较复杂的度规
（见方程二）
！而且它很重要，因为它描述了坍缩恒星的最终态——它们总是具有非零的角动量。
○
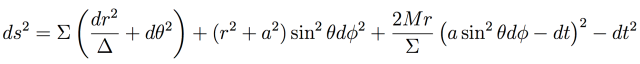
方程二：克尔
解描述了一个旋转的黑洞。
我们现在比较确定的是宇宙中遍布着许多的黑洞。正如同钱德拉塞卡
（Chandrasekhar）
，托乐曼
（Tolman）
，奥本海默
（Oppenheimer）
和沃克尔夫
（ Volkoff）
在上个世纪30年代说的那样，如果太多的质量聚集在一起，则没有任何力能维持住它们。确切的数字还比较难弄清楚，但大约是如果一颗已经耗尽所有核燃料的恒星质量达到3个太阳质量，那么它将会坍缩成黑洞。远不止这些，还有更令人惊奇的，在星系中间存有更大的黑洞。在银河系的中心就居住着一个黑洞，其质量大约为400万个太阳质量。我们没在逗你！现在的共识是，许多星系在他们的中心有质量高达数十亿太阳质量的
超大质量黑洞
。我们不知道这些黑洞是如何形成的，但对银河系来说，我们可以通过追踪个别恒星的轨道并观察黑洞引力的影响来确定它的存在。
○
图二：星系中央的超大质量黑洞正在吞噬周围的物质（艺术渲染图）
。
|
图片来源：NASA
探测
引力波
的 LIGO 装置简直是棒极了。 LIGO 是一个大型的
迈克尔逊干涉仪
，单边的测量距离是四公里。 LIGO 是“激光干涉引力波天文台”的缩写，激光是一些完美得惊人的单色光源，非常集中且高能，我们可以用它来焊接金属，但又很便宜，我们能将它们用于现代唱片机，来代替传统的那根针。虽然我们还没能力造出会飞的汽车，但拥有了激光这个挺厉害的东西。总而言之，LIGO 刚刚完成一个严肃的科学活动，它几乎是意外地捕捉到这个近乎完美的引力波形，并与描述两个质量约为30个太阳质量的
黑洞合并
的模型吻合。
每个人都被广义相对论惊艳，因为它成功地描绘了时空被撕扯成碎片的黑洞附近强场区域，以及微弱的引力波轻轻划过时空的远场区域。
○
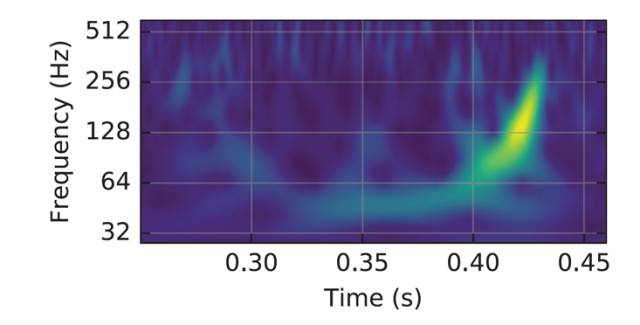
图三：引力波的直接证据
。
|
图片来源：LIGO Scientific Collaboration
您的另外一个已经走了很远的想法是
宇宙学常数
。尽管您把它称为是您最大的错误，但我们现在认为这是对您的场方程的一个小修正
（见方程三）
。这在长距离尺度上是很重要的：天文学家无法解释宇宙为什么会加速膨胀，除非宇宙中约70%的能量都来自宇宙学常数，又或是来自于我们所说的“
暗能量
”。暗能量驱使着宇宙呈指数式膨胀，而非最初您提出宇宙学常数时所希望保持的静态宇宙。在另一方面，为了追寻统一理论，在大量对时空的研究中都采用了负宇宙学常数。具有负宇宙学常数的五维广义相对论与四维时空边界上的量子理论能自然的连接在一起，几乎就好像量子理论是广义相对论的一个映射！
○
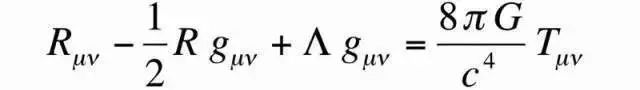
方程三：
为了描述静态的宇宙，爱因斯坦在场方程中引进了宇宙学常数（Λ）。
我们现在非常确定量子理论是正确的
（抱歉）
