生活中的误区：看检查结果，得病的可能性是95%吗？

一个25岁的很健康的青春靓丽的女孩去医院做检查，验血后发现她可能患有白血病。医院又告知，验血的结果有95%的可能性是可靠的，换言之，有5％的可能是误诊。顿时，这个妙龄少女几乎万念俱灰，她想肯定是有白血病了。而且大多数人甚至包括医生们都认为她的白血病的可能性是95％。天哪，真的是这样吗？你也认为她得病的可能性是95%吗？如果不是95%，那你认为究竟是多少？问题出在哪里？

思考ing......

实际上，这个可能性远没有95%这么高。为什么呢？

因为人们在得出95%的结论时没有考虑到先验概率！事实上，如果考虑了先验概率的话，这位女孩完全不必这么担心。实际上医院知道25岁的女孩中得白血病得可能性是非常之低的，就算夸张一些，用0.1%来计算，也可能算出只有这个验血结果的信息下，她得病得概率会小得让大家吃惊。那么，到底会是多少呢？

这时，必须求助于万能的贝叶斯先生。正好我们前些日子创作了一篇《真的理解贝叶斯公式吗？》，文中阐述了一个观点：

理解和运用贝叶斯公式的关键是：理清问题中的规律和现象！

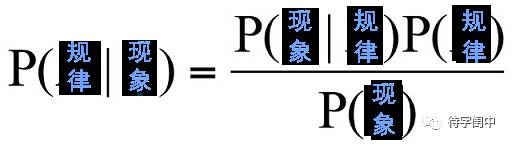
根据这个诀窍，那么我们来看看上述场景中的规律和现象。

两个规律（结论）：有白血病，无白血病。两个现象（测试结果）：验血有白血病，验血无白血病。根据场景中的描述，P(有白血病)=0.001，P(无白血病)=0.999，P(验血有白血病|有白血病)=0.95，P(验血无白血病|有白血病)=0.05，P(验血有白血病|无白血病)=0.05，P(验血无白血病|无白血病)=0.95。再，假设有1000个女孩，由于P(有白血病)=0.001，所以其中1个有白血病，999个没有白血病，再者，有95%的可能性是可靠的，那么P(验血有白血病)=(1*P(验血有白血病|有白血病)+999*P(验血有白血病|无白血病))/1000=(1*0.95+999*0.05)/1000=0.0509。

那么，根据贝叶斯公式，得到：

P(有白血病|验血有白血病)=P(验血有白血病|有白血病)*P(有白血病)/P(验血有白血病)=0.95*0.001/0.0509=0.01866＝1.9%。

不到2%，虚惊一场。

真是，生活中的贝叶斯无处不在，但是，人们常常犯错，不按贝叶斯的方式来思考。