最近在研究个人所得税的收入再分配效应,不是心甘情愿的,毕业论文需要

因为使用了CHIPS的数据库,微观住户调查数据是我见过最变态的数据源,没有之一~
其中所使用到的理论模型中需要计算很多个人所得税、再分配效应和累进性指标,经过参考各方文献资料,依靠着自己对于R语言的一丁点儿基础,终于把所有的指标计算代码整理完了,因为代码太多,除了预处理和数据清洗的之外,这里分享一下我觉得可能会对学术研究人员有用的几段核心代码!
以下代码一共分为两类,一类是计算个人所得税的代码,一类是衡量收入分配不均等的测度指标。
个人所得税:
大家都知道,我国现行的个人所得税是分类征收的,11个类别,但是通常计算比较复杂的是带有费用扣除和累进税率的收入类型,这里我仅以典型的工资薪金收入所得和经营性所得的应纳税额计算为例,按照最新税法标准计算,其他的类别大多都执行比例税率,计算较为简单。
工资薪金所得税:
其中的Salary表示工资薪金收入;Three_one表示三险一金;tax_Salary表示应纳税所得额。因为我拿到的工资薪金收入是全年的,所以算了月均应纳税所得额,实际中个人所得税都是按月缴纳的,所以计算应纳税所得额的时候,需要自己修改一下以下语法:
计算工资薪金所得收入应纳税所得额:
house_2013_data$tax_Salary
工资薪金所得收入应纳税所得额:
house_2013_data0 & tax_Salary<=1500] =tax_Salary[tax_Salary>0 & tax_Salary<=1500 ] *.03
Salary_tax[tax_Salary>1500 & tax_Salary<=4500] =tax_Salary[tax_Salary>1500 & tax_Salary<=4500 ] *.10-105
Salary_tax[tax_Salary>4500 & tax_Salary<=9000] =tax_Salary[tax_Salary>4500 & tax_Salary<=9000 ] *.20-555
Salary_tax[tax_Salary>9000 & tax_Salary<=35000] =tax_Salary[tax_Salary>9000 & tax_Salary<=35000] *.25-1005
Salary_tax[tax_Salary>35000 & tax_Salary<=55000] =tax_Salary[tax_Salary>35000 & tax_Salary<=55000] *.30-2755
Salary_tax[tax_Salary>55000 & tax_Salary<=80000] =tax_Salary[tax_Salary>55000 & tax_Salary<=80000] *.35-5505
Salary_tax[tax_Salary>80000] =tax_Salary[tax_Salary>80000]*.45-13505 })
house_2013_data$Salary_tax
经营性净收入应纳税额计算:
Business_F(个体工商户的生产经营活动、企事业单位的承包经营、承租经营活动)
tax_Bussiness指经营性收入的应纳税所得额,经营性收入按年度缴纳。
house_2013_data$tax_Bussiness0 & Business<=15000 ] =Business[Business>0 & Business<=15000 ]*.05
Business_tax[Business>15000 & Business<=30000 ] =Business[Business>15000 & Business<=30000 ]*.10-750
Business_tax[Business>30000 & Business<=60000 ] =Business[Business>30000 & Business<=60000 ]*.20-3750
Business_tax[Business>60000 & Business<=100000] =Business[Business>60000 & Business<=100000]*.30-9750
Business_tax[Business>100000]=Business[Business>100000 ]*.35-14750})
因为个人所得税的计算肯定是要给纳税人打标签的, 即算出来的应纳税额必然要与纳税人的ID一一对应,所以我直接用了含有税前收入的数据框作为函数的参数,具体运用的时候,记得你的数据框中必须要有同名的变量,或者可以修改上述代码中税前收入的变量名,改成与你的含税前收入的数据框税前收入名称一致即可。
收入不平等指标:
基尼系数:
Ginifunction(income){
library("caTools")
cum_income return (A/(A+B))
}
其几何解释如下图所示:
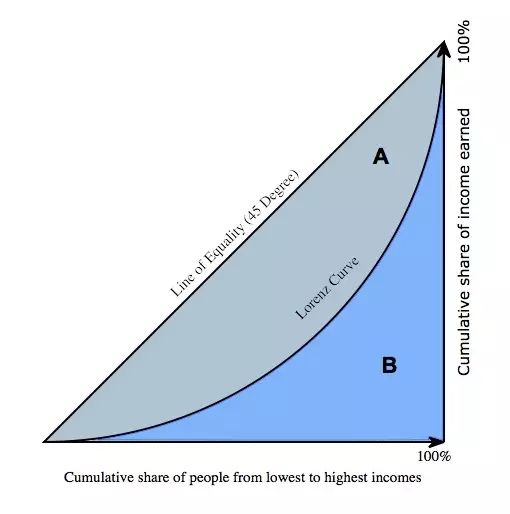
以上基尼系数的代码是本人根据基尼系数几何法原理,同时参考了 知乎大神@何世提的Python版本思路,使用前提出几点建议,基尼系数对0值和负值极度敏感,倘若你的收入收入中含有零值和负值,最好提前做清洗处理,虽然理论上来说,零值和负值的确也能解释的通。
import numpy as np
def gini_coef(wealths):
cum_wealths = np.cumsum(sorted(np.append(wealths, 0)))
sum_wealths = cum_wealths[-1]
xarray = np.array(range(0, len(cum_wealths))) / np.float(len(cum_wealths)-1)
yarray = cum_wealths / float(sum_wealths)
B = np.trapz(yarray, x=xarray)
A = 0.5 - B
return A / (A+B)
以上Python版本来自于知乎知名话题答主何史提大神:
作者:何史提
链接:https://www.zhihu.com/question/20219466/answer/25936162
再分配效应指数:
再分配效应,也即MT指数,用于衡量一项税收政策对收入不平等的影响程度,其经过多年发展,出现了很多分解公式,已经衍生了很多附属指标,这里我将与其有关联的累进性指标P指数也同时纳入MT指数的算法中:
所用到的内置函数:
Ginifunction(income){
library("caTools")
cum_income return (A/(A+B))
}
Gini_Nfunction(income){
library("caTools")
cum_income return (A/(A+B))
}
MT指数
MTfunction(Salary_gini_data){
library(dplyr)
GX%arrange(Salary)%>%.[,"aftertax_salary"]%>%Gini_N
t return(data.frame(Name=c("税前尼基系数","税后基尼系数","税收集中度","税后收入集中度(按照税前收入排序)","平均税率","应纳税所得额集中率","MT指数","累进性指数","横向公平效应","纵向公平相应","免征额累进性","税率结构累进性"),
Index=c("GX","GY","CT","CY","t","CXT","MT","P","H","V","Ded","Ratio"),
Scale=c(GX,GY,CT,CY,t,CXT,MT,P,H,V,Ded,Ratio)
))
}
MT公式的参数仍然是一个数据框,数据框中的四个必备变量是:
Salary:税前收入;
Salary_tax:tax_Salary;
Salary_tax:应纳税所得额;


















