来自:暮回 - 51CTO技术博客
链接:http://muhuizz.blog.51cto.com/11321490/1878366
(点击尾部阅读原文前往)
已获转载授权
首先给出五道关于二叉树的面试题,题目很简单,这里会给出简单分析,具体代码,这里只给出最优解法。
◆找出二叉树中最远结点的距离
◆由前序遍历和中序遍历重建二叉树
◆判断一棵二叉树是否为完全二叉树
◆求二叉树中两个结点的最近公共祖先
◆将二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
 找出二叉树中最远结点的距离
找出二叉树中最远结点的距离
首先需要考虑一下,二叉树中什么距离是最远距离。以根节点为轴,左右子树的最大深度?当然这只是一部分。准确地说,最大深度是以根节点为轴,左右子树的最大深度之和与以各个子树的根节点为轴左右子树的最大深度之和的较大值。
虽然有点绕,看下图就会明白。
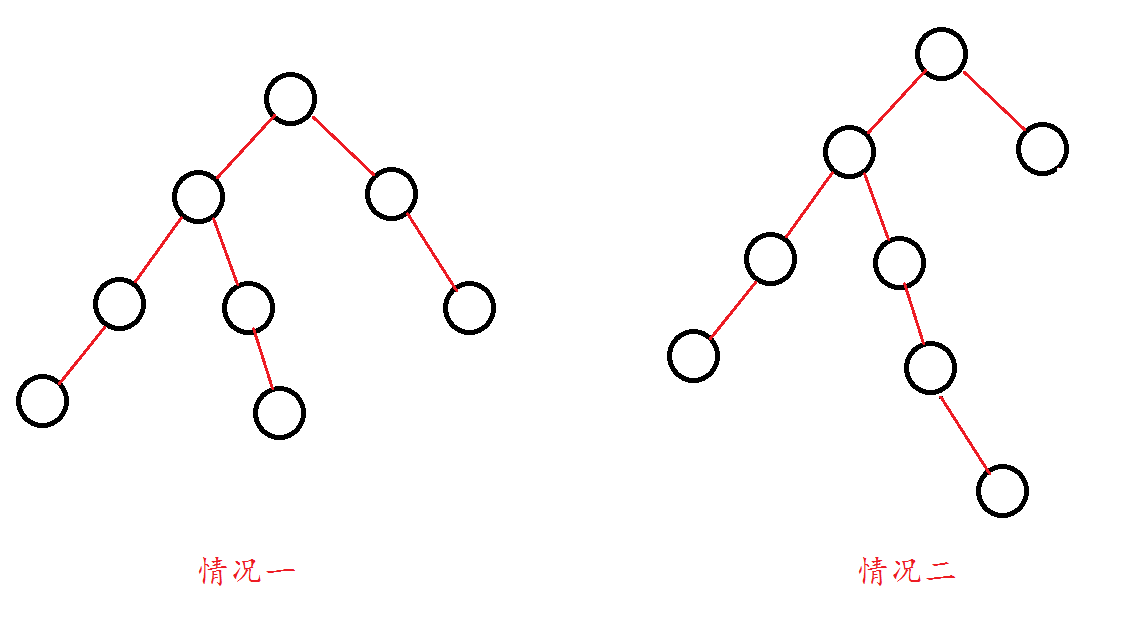
思路一:
解决这个问题最直接的方式就是遍历。对每个结点求深度,之后再与保存的最大深度max_depth进行对比,但对于O(n^2)的时间复杂度,我们还是选择能避免就避免,这应该是一种比较糟糕的时间复杂度。
思路二:
针对思路一,可以发现,我们重复了大量的遍历工作。对每一个结点求深度,对最深的一个结点遍历了n^2次,没有线索化过的二叉树遍历,最常用的是递归方法,因此,我们可以仅仅通过一次递归,同时得到该结点的深度和以该节点为根的子树的最大距离。当然,由于深度是相对整个遍历过程的,因此在递归过程中,它应该是以引用的方式进行传递,我们这里不需要将深度也作为一个参数进行传递,原因很简单,深度完全可以在递归的时候用返回值接收,这也解决了对左右子树深度的比较选取的过程中多余创建出的变量。
int MaxDistance()
{
if (_root == NULL)
return 0;
int max = 0;
_MaxDistance(_root, max);
return max;
}
int _MaxDistance(Node* cur, int& max)
{
if (cur == NULL)
return 0;
int leftDepth = _MaxDistance(cur->_left, max);
int rightDepth = _MaxDistance(cur->_right, max); if (leftDepth + rightDepth > max)
max = leftDepth + rightDepth;
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
代码看上去很简单,这里巧妙之处在于在MaxDistance()函数中,我们没有用它调用的_MaxDistance()函数的返回值,该函数返回值的作用,仅仅是为了提供递归返回使用。我们需要的max_distance是通过传递引用的方式获取的。
 由前序遍历和中序遍历重建二叉树
由前序遍历和中序遍历重建二叉树
这道题应该是网上做烂的题目,这里只是重新提一下,因为它并没有什么建档方法可言。
我们需要考虑,前、中、后序遍历三种方式遍历结果有什么特点。
前序遍历:
第一个元素必然是根节点,扩展一点将,如果我们从前序遍历的序列中取出的一段属于某个子树的前序遍历段,那么该子序列的第一个结点也将是该子树的根节点。
中序遍历:
中序遍历由于是先左后根,最后再右的顺序,因此,当我们知道某个结点为跟结点的话,那么它的左右两侧分别是左子树和右子树的中序遍历序列。同上,也扩展一点将,只要可以找到某一段子树中序遍历序列的根节点,那么该序列中,跟结点的左右两侧序列也是该子树的左右子树。
后续遍历:
后续遍历的特点是遍历完左右结点之后再遍历跟结点。和前序遍历的区别就在于把根节点放到了最后访问,因此,两种遍历的结果类似,只不过需要从后向前依次取元素。也就是说,最后一个元素,是当前树的根节点。
经过上面的分析,我们可以得出一个这样的结论,如果我们想重建二叉树,我们至少需要两种遍历的序列,而且必须要有中序遍历序列。
接下来我们讨论如何利用前序和中序遍历的结果重建二叉树。大致可分为以下四步:
1、用前序序列的第一个结点作为根结点;
2、在中序序列中查找根结点的位置,并以此为界将中序序列划分为左、右两个序列(左、右子树);
3、根据左、右子树的中序序列中的结点个数,将前序序列去掉根结点后的序列划分为左、右两个序列,它们分别是左、右子树的前序序列;
4、对左、右子树的前序序列和中序序列递归地实施同样方法,直到所得左、右子树为空。
下来看实现代码。
typedef BinaryTreeNode Node;
Node* ReBuildTree(const string preorder, const string inorder)
{
if (preorder.empty())
return NULL;
char root_value = preorder[0];
Node* node = new Node(root_value);
size_t index = inorder.find(root_value);
string left_preorder = preorder.substr(1, index);
string left_inorder = inorder.substr(0, 3);
string right_preorder = preorder.substr(index + 1, preorder.size() - index - 1);
string right_inorder = inorder.substr(index + 1, inorder.size() - index - 1);
node->_left = ReBuildTree(left_preorder, left_inorder);
node->_right = ReBuildTree(right_preorder, right_inorder);
return node;
}
void InOrder(Node* node)
{
if (node == NULL)
return;
InOrder(node->_left);
cout _data " ";
InOrder(node->_right);
}
仔细观察可以发现,这里使用的容器是string,我这里选用string作为容器,是因为string有自带的查找某个元素的功能,同时可以实现部分截取,方便构建子序列,缺点就是每个结点中key的类型只能是字符。当然,这里也可以选用vector等其他容器,只不过vector没有内置的Find函数,因此在中序遍历序列中找根节点的时候需要进行遍历,vector构建子序列时也并不复杂,可以通过迭代器区间直接构造一个vector对象。这里点到为止。
 判断一棵二叉树是否为完全二叉树
判断一棵二叉树是否为完全二叉树
首先需要知道的是什么是满二叉树。若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
判断一棵树是不是满二叉树,就不能再像之前那样,递归去遍历,因为递归是在走深度,所以解决这一问题,需要借助queue完成层序遍历。
我们简单的层序遍历是先将根节点入队列,之后依次访问队列的front结点,访问完成,将front结点pop,同时将左右不为空的子节点入队列,直到队列为空。这一点应该没有太大问题。回想一下,我们在简单层序遍历的时候,注意了什么问题?如果子结点为NULL,则不入队列,防止下次对空结点进行访问 。
回到我们一开始的问题,判断一棵二叉树是否为满二叉树。这里在简单层序遍历上做一些处理,先不考虑队列的问题,当我们简单地在走层序遍历过程中,当碰到一个结点为NULL时,如果之后都是空结点,那么该二叉树为完全二叉树,否则,不满足完全二叉树。
因此,要实现这个逻辑,就不能只是简单地把非空结点入队列,所有结点都需要入队列,当front变为NULL时,表示读取到了一个空结点,此时,它的子节点之前的所有结点都已经入队列,当队列中还存在空结点,则该树不满足满二叉树。
代码实现如下:
bool IsFullBinaryTree()
{
if (_root == NULL)
return true;
queue que;
que.push(_root);
Node* front = NULL;
while (front = que.front())
{
que.push(front->_left);
que.push(front->_right);
que.pop();
}
while (!que.empty())
{
if (que.front() != NULL)
return false;
que.pop();
}
return true;
}
 求二叉树中两个结点的最近公共祖先
求二叉树中两个结点的最近公共祖先
第一次看到这道题,感觉无从下手,后来仔细想想,不是废话么,只告诉了要找最近公共祖先,二叉树的特点都不知道,怎么找......没办法,分情况看。
情况一:搜索二叉树
这应该是最简单的情况了,搜索二叉树始终满足根结点大于左孩子,小于右孩子。那他们的公共祖先的key值就必然介于两个结点之间。即
(root->_data >= node1->_data && root->_data _data)
||(root->_data >= node2->_data && root->_data _data)
因此,这样一来就简单了很多,代码实现如下:
typedef SearchTreeNode Node;
Node* FindParent_SearchTree(Node* node1, Node* node2, Node* root)
{
if (root == NULL)
return NULL;
if (node1 == NULL)
return node2;
if (node2 == NULL)
return node1;
while (1)
{
if(root === NULL)
assert(false);
if ((root->_data >= node1->_data && root->_data _data)
|| (root->_data >= node2->_data && root->_data _data))
{
return root;
}
else