
随着我们生活水平的提高,人们已经渐渐地不像过去那样担心温饱问题了,每天山珍海味的生活也不再稀罕——午餐来一顿正宗的羊杂火锅,晚餐煎两块半熟的神户牛排,再和三五好友撸几串烧烤作为夜宵,拍个照发发朋友圈,大快朵颐又格调十足的一天就这么过去了。正是:
新酒陈酿交相伴,
鸡鸭鱼虾齐聚欢。
华灯阑珊辗转夜,对月撸串颜芳绽。

自然灾害时期。图中大肚子小朋友因长期营养不良,患有夸休可尔症(Kwashiorkor)

如今享用这样的美食已不再是难事
不过值得注意的是,尽管美味珍馐并不难得,健康的身体却更加重要。忍饥挨饿会造成营养不良,但饮食不加控制却可能带来一种“富贵病”——糖尿病。根据WHO(世界卫生组织)的调查[1],截止2016年,我国有1.1亿
(差不多10%)
的人患有糖尿病,将近四成成年人处于糖尿病前期[11]。
身体是革命的本钱,而国人对身体健康的关注度也日益提高。就糖尿病问题而言,控制血糖是关键,那么人体是如何调控血糖的呢?这得从著名的
胰岛素
说起。
一、胰岛素的来源——
β
细胞
中学生物课告诉我们,
胰岛素
(Insulin)
在血糖控制中起着决定性的作用。因为尽管胰高血糖素
(Glucagon)
、肾上腺素
(Epinephrine)
和可的松
(Cortisol)
等由不同腺体分泌的激素都能使血糖
直接
升高,胰岛
β
细胞分泌的胰岛素却是目前发现的
唯一能够直接降低血糖的激素
[2]。
我们都知道,糖尿病和胰岛素紧密相关。事实上糖尿病可以分为I型
(胰岛素分泌缺陷
,多为先天型
)
和II型
(胰岛素利用效率不高,多为后天型)
[3]
,都和胰岛素有关。
那么到底是什么造成了胰岛素的异常分泌呢?这是由于
β
细胞的胰腺细胞代谢紊乱而造成的,因此了解
β
细胞的作用原理是理解血糖控制机理的关键。
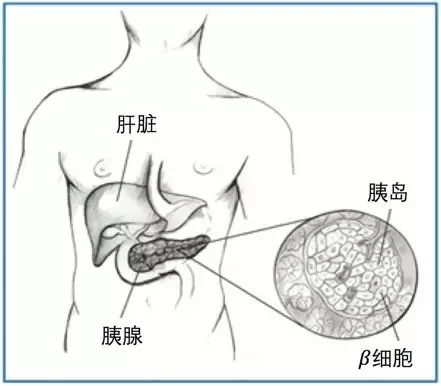
图一:
β
细胞存在在胰腺中的胰岛部分
由于
β
细胞既能产生激素,又像神经细胞一样能产生细胞
膜电位
(又称为动作电位)
,
β
细胞是
神经内分泌细胞
(Neuroendocrine Cell)
的一种
。小编在《
读懂你的大脑——漫话神经元
》(
传送门
)中提到,神经细胞在收到刺激后膜电位会发生变化从而产生
神经脉冲
,我们来温习一下神经细胞膜电位变化的原理:
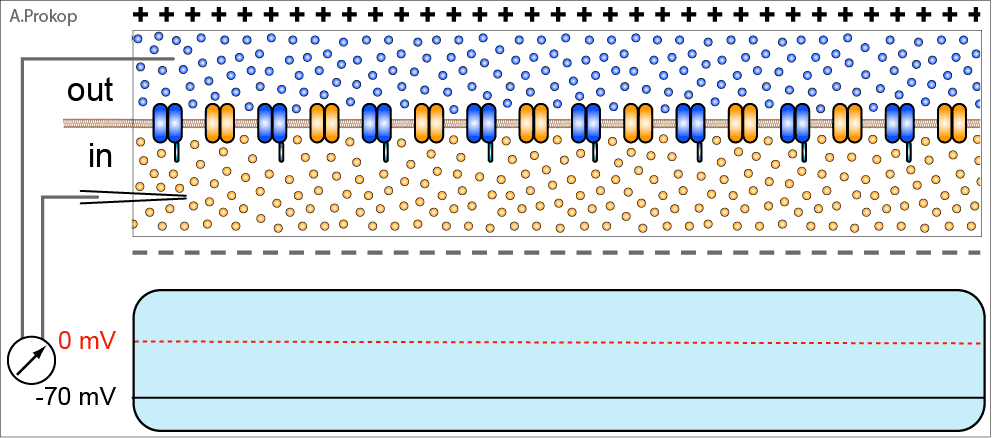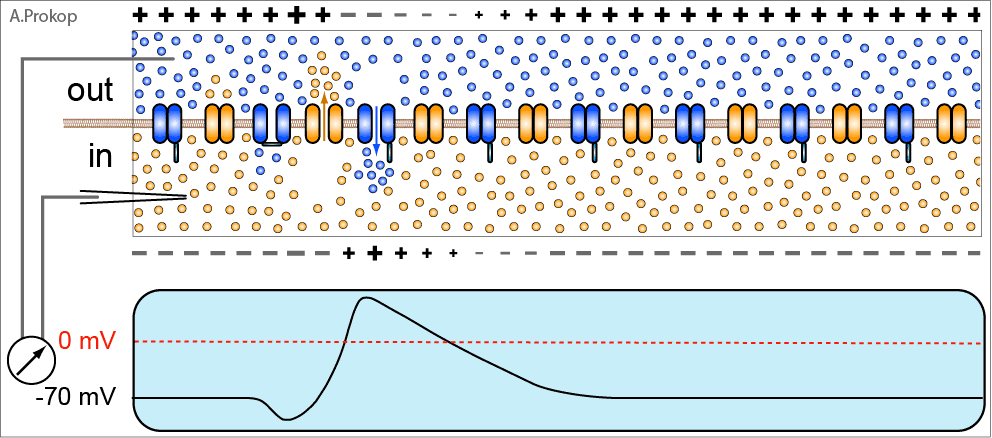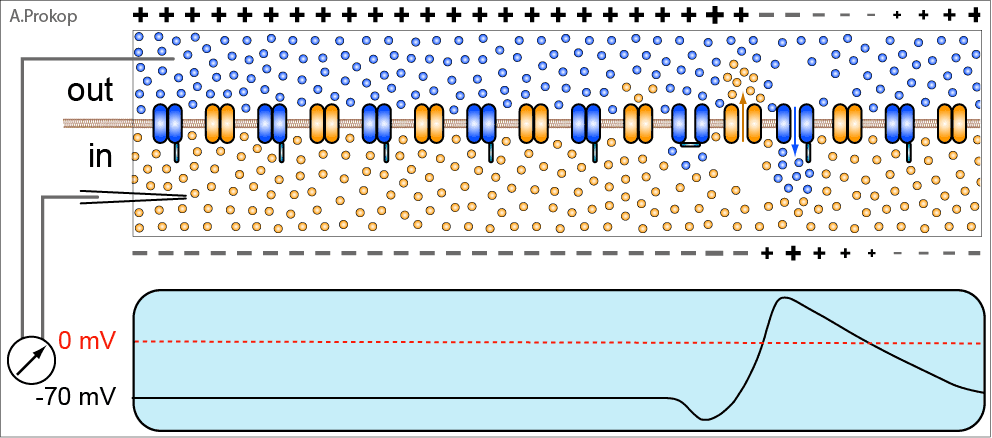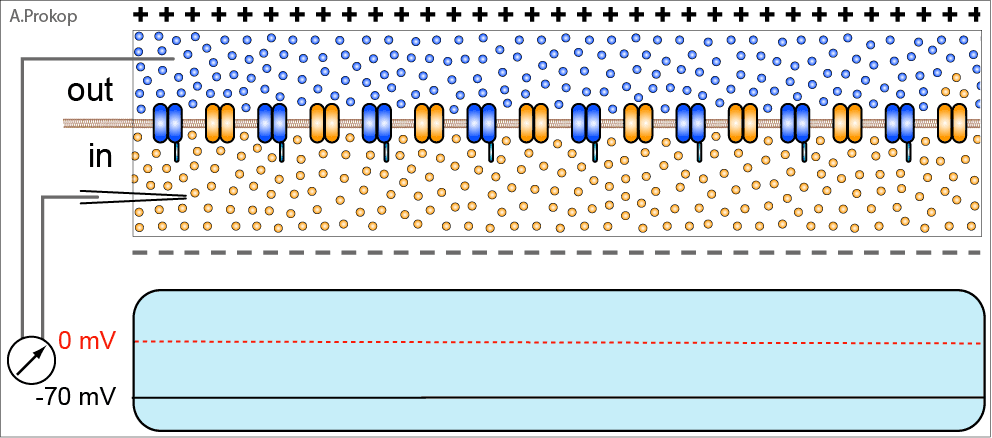
动图一:神经脉冲产生于细胞膜内外离子的交换
单个神经元完整的神经脉冲序列大概是这样的:
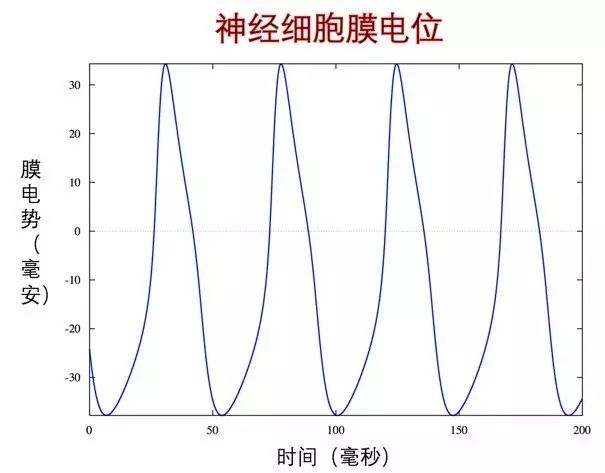
图二
因此神经细胞产生神经脉冲时就好像跳华尔兹一样,一切步法都跃然于纸上,有章可循。神经内分泌细胞虽然也有一半血缘是来自神经细胞,也能产生神经脉冲,不过它们产生脉冲方式的却很有个性:
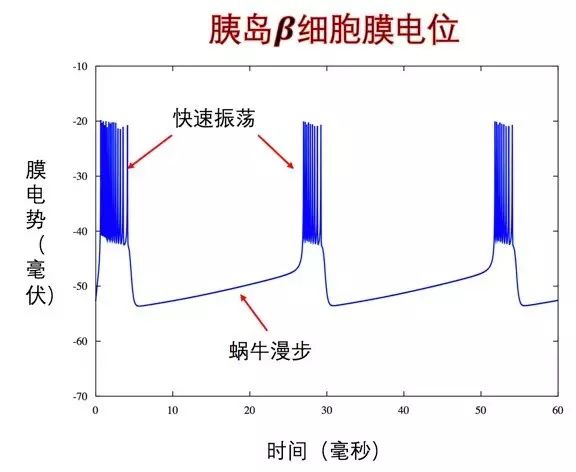
图三
很显然,以
β
细胞为首的神经内分泌细胞并不喜欢循规蹈矩的华尔兹,而喜欢在平缓如蜗牛的步法中骤然加几组狂风骤雨般的狂野,而后又继续如蜗牛般漫步。有条不紊中洋溢着青春激情,这造就了神经细胞和神经内分泌细胞的本质差异。在生物学领域,神经内分泌细胞的这种脉冲又称之为
爆破脉冲
(Bursting)
。
那么
β
细胞是如何产生爆破脉冲的呢?这和胰岛素的分泌又有什么关系呢?接下来小编将用数学模型来揭示其中的本质。
二、数学模型再次登场
小编在《
读懂你的大脑——漫话神经元
》(
传送门
)一文中提到了获得过1963年诺贝尔生理学或医学奖的Hodgkin-Huxley模型,用来描述如下图所示:

图四
如果看到这个方程后,你的表情是这样的:

不必感到心慌,事实上我们只需要了解它的核心就绰绰有余了——
膜电位完全由细胞内外离子浓度差所决定
。所以荣获1963年诺贝尔生理学奖的
Hodgkin-Huxley模型
,本质上就是
欧姆定律
(I = C*V/t)
。

图五
在上面这个方程中所出现的离子只有
钾离子
和
钠离子
;而在神经内分泌细胞中却需要考虑
钙离子
的作用。
同水、二氧化碳这些小分子,以及脂肪酒精等脂溶性分子不同,自由离子多是大块头,想要横穿细胞膜
(磷脂双分子层)
就必须通过“柜台窗口”——
离子通道
(Ion Channel)
。银行里的不同柜台窗口办理不同业务,例如存取款、投资理财、办理财产证明等,不在其位不谋其政;同样的道理,不同离子只能穿过特定的离子通道。银行柜台会随着客流量大变化而新开或关闭,细胞膜上的这些离子通道也会审时度势,随着离子浓度变化伺机开启或关闭。
和神经细胞不同,
β
细胞
膜上存在钙通道,并且钾通道比神经细胞多一种。因此,描述
神经内分泌细胞膜电位的方程就需要改一下了:
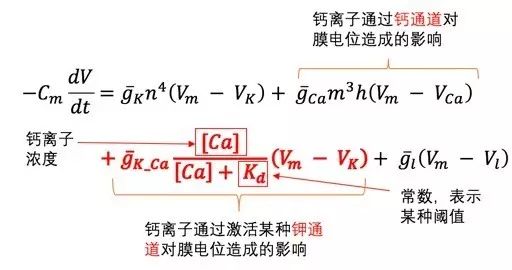
图六:
从数学观点看来,和第一个方程相比,主要区别是钙也能影响钾离子通道的闭合
当然我们还要考虑
β
细胞内
钙离子浓度的变化情况。钙离子非常擅长社交活动,人脉极广,因此在
细胞外、线粒体、内质网、高尔基体甚至酶和激素上面等都可以看到它的身影。为了简化问题,我们考虑最简单的
钙离子浓度方程[4]:
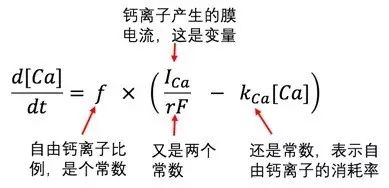
图七
那么上面这个方程的解是怎样的呢?在选取适当参数以后,小编用了一个叫做"XPP"的计算软件进行模拟
(尽管该软件UI界面颇有历史沧桑感,但计算效率很高
),方程代码参见[5],画图代码参见[6]
:

动图二
:爆破脉冲,
是不是很像心电图和肌电图?
神奇的是,自从有了钙离子这个社会活动家的加入,我们竟然观察到了
β
细胞的
爆破型脉冲!那么钙离子扮演了怎样的角色呢?我们来看看膜电位和钙离子浓度之间的变化关系:
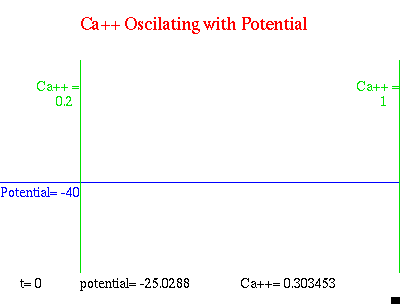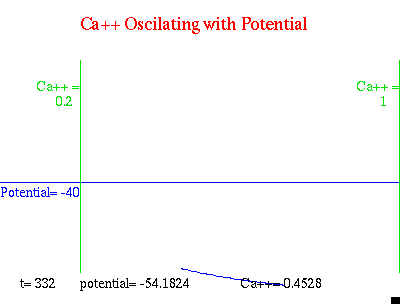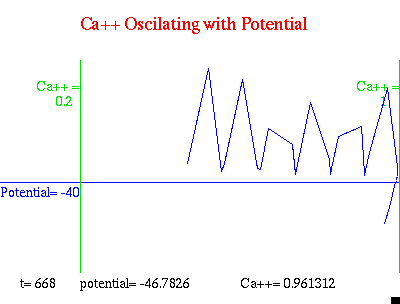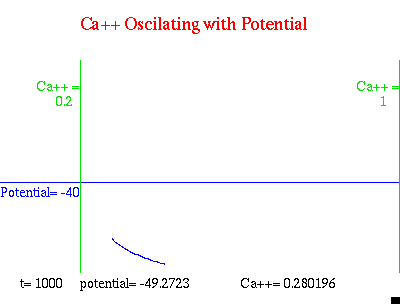
动图三
可见无论膜电位是快速振荡还是跳华尔兹,细胞内钙离子浓度都控制在一个范围内,且变化幅度不紧不慢,有些“一蓑烟雨任平生”的味道。因此我们可以通过这个数学模型作出预测:当钙离子浓度过小或过高
(小于0.2μM或大于1μM)
时,都可能使胰岛素分泌不足。
不过在数学上,这个模型还有两点值得注意:
-
这个预测准确的前提是,
模型参数需要正确选取
。
如何选取模型参数是一个很宏大的话题,已超出本文范畴。小编会在以后的文章中继续介绍,大致情况可参见小编之前的一篇文章[7]。
-
这个方程组的一个特殊之处在于,不同化学反应在时间尺度上存在很大差异,这是使得膜电势得以在快速振荡和跳华尔兹两种状态之间相互转换的重要原因。这类时间尺度不一的问题在计算科学中被称为
刚性问题
(Stiff Problem)
。要模拟这一类问题的解,一般的向前欧拉法或龙格-库塔方法会造成解的不收敛,因此需要采用向后欧拉法等隐式方法。
三、模型的分析——钙离子如何诱发爆破脉冲?
小编在上一篇文章《混沌理论到底是什么——从蝴蝶效应出发》[8](
传送门
)中强调了
分歧理论
(Bifurcation Theory)
在混沌理论中的重要地位。事实上,
β
细胞的
爆破型脉冲的产生原因,可以完全由分歧理论解释。
什么是分歧理论?答案只有一句话——
系统(方程)参数的变化诱使系统
(方程)
解的稳定性发生变化
。
爆破型脉冲是如何产生的?答案同样只有一句话——
钙离子浓度的缓慢变化使得模型发生霍普夫分歧
(Hopf Bifurcation)
。
所谓霍普夫分歧,就是指随着参数的变化,系统
(方程)
的解从平衡态解
(Equilibrium Solution)
而突然酝酿出一个周期解
(Periodic Solution,从几何角度看来,周期解就是极限环)
:
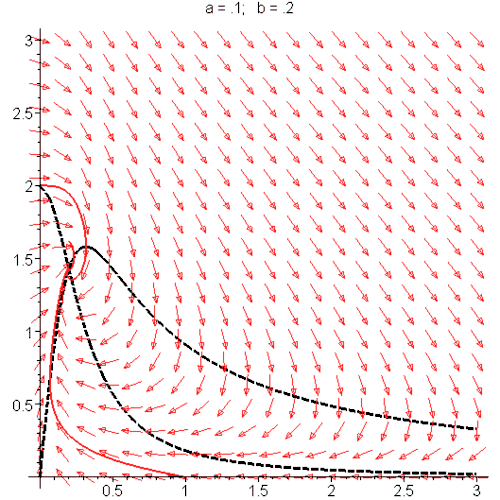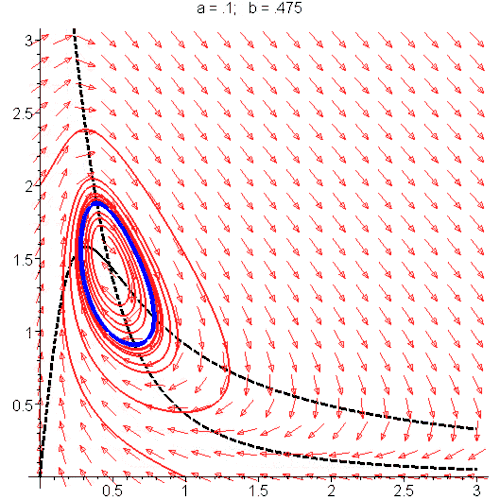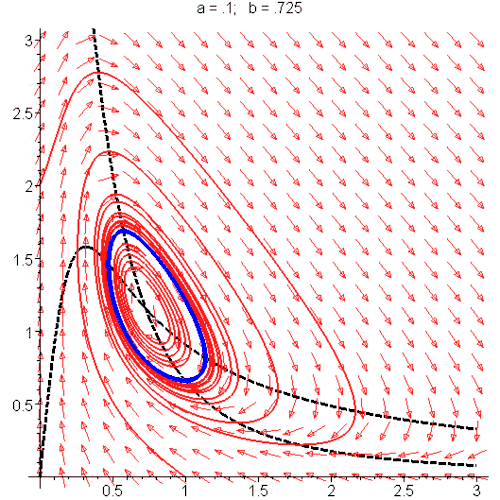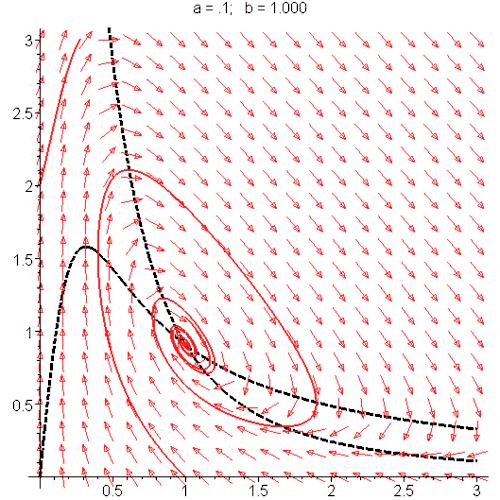
动图四:
蓝色的圈就是周期解,或极限环(limit cycle)
我们来看看
β
细胞方程解是如何随着钙离子浓度发生变化的:
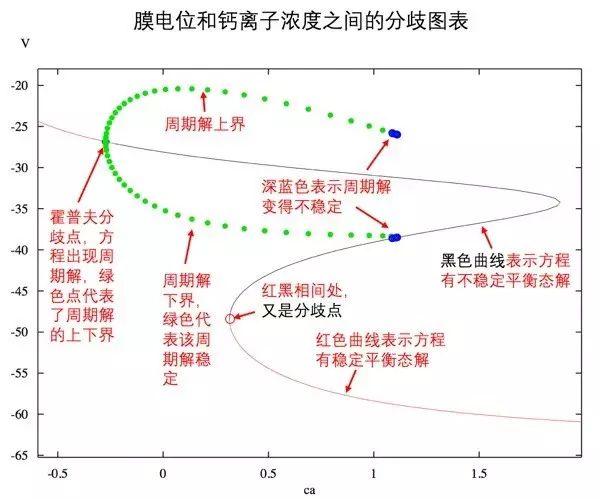
图八
注意上图实际上有两个分歧点,其中一点意味着单点解稳定性的变化,这样的分歧称之为
鞍点分歧
(Saddle-Node Bifurcation)
。一些读者可能在其他场合也听到过“鞍点”这个概念,其实在数学中所有的鞍点定义的本质都是一样的,即
对应矩阵
(或算子)
特征值有正有负
,而矩阵
(或算子)
特征值的正负性则完全决定了方程解的局部稳定性。不过,这里我们更关心霍普夫分歧点。
上面这个分歧图表还有什么其他用途呢?事实上如果加上钙离子的浓度变化方程
(见图七)
,即把上一部分的动图添加到分歧图表中,一切就明白了:
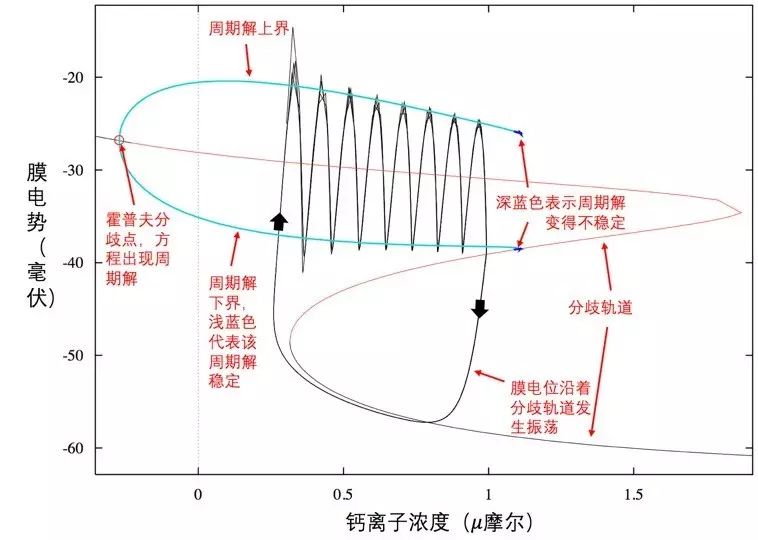
图九
所以在实际情况中,方程解的变化完全由分歧图表所决定:膜电势的快速振荡幅度由浅蓝色曲线确定,它想静下来缓步前行也得顺着分歧轨道走。
当爆破脉冲行进到深蓝色曲线附近时,由于周期解变得不稳定,于是膜电势从快速振荡轨道撤退到了稳定轨道,开始沿着稳定轨道蜗牛漫步了。
膜电势的一举一动都牢牢掌握在分歧图表当中。
四、完整的故事
目前为止我们已经弄清楚了胰岛素分泌过程最关键的一环——
β
细胞膜电位的爆破型脉冲。但目前为止我们只着重考虑了钙离子的浓度,那么这又和血糖有什么关系呢?胰岛素分泌以后又是怎样发挥作用的呢?
概括地讲,答案各只有一句话——血糖变化能改变
β
细胞模型
(图六)
中的各个参数;而胰岛素通过促进生成
第四类
葡萄糖转运体
(GLUT4)
把血液中的葡萄糖合成为糖原,从而降低血糖。但其中涉及到很多细节,分别可参考文献[9]和[10]。
例如胰岛素是这样影响第四类葡萄糖转运体
(GLUT4)
合成的:
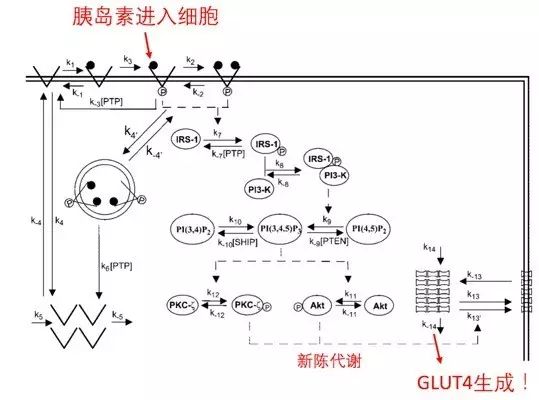
图十:胰岛素如何发挥作用
因此要想描述以上过程,需要解一个变量较多的方程组:

图十一:方程变量虽多,但都大同小异
整个过程看似很复杂,但每一步条理都是非常清晰的。现在我们可以来总结一下血糖调整的完整过程了:
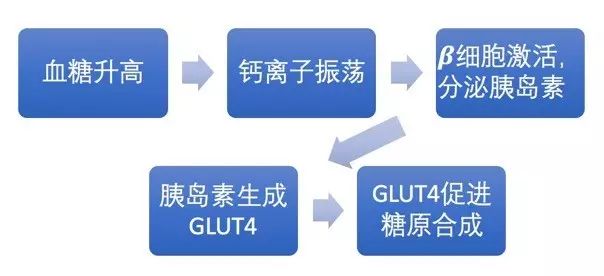
图十一
五、化繁为简才是硬道理
通过本文的分析,读者们已经深刻感受到了生物世界的复杂性。事实上复杂性无处不在,不仅限于生物领域,而如果用数学观点来看待这些问题,一切都能变得有条有理,这便是数学模型价值之一。
好的数学模型总是能够有效化繁为简。例如在数学家眼中,
β
细胞的方程还可以简化成为:
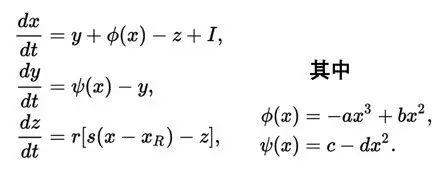
这又被称之为Hindmarsh–Rose模型,它和小编在[8]中提到过的罗伦兹模型很像,只不过不同的
参数选择
(
Hindmarsh–Rose模型r参数取值很小
)
和不同的
非线性项
使得两个方程组解的表现大相径庭——
Hindmarsh–Rose模型产生周期性的爆破脉冲,而
罗伦兹模型却产生混沌解。如此简单的一阶非线性常微分方程就能产生许多有趣的结果,更不用说更加复杂的偏微分方程和随机微分方程了。
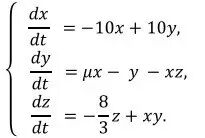
罗伦兹模型
数学模型的另一个价值在于,它能对自然科学中的各种现象给出合理的解释,甚至给出定性和定量的预测,这对处理数据、指导实验方向等有着重大意义。当然,数学模型也离不开实验的支持,因为模型参数的选取非常依赖具体的实验数据。实验和数学模型双剑合璧,相互取长补短,
能够使科学发展少走很多弯路。
回到生物学的范畴。生物领域中的未解之谜数不胜数,尤其是细胞和分子层面的生物各种代谢反应和形态发生等,这涉及到几乎所有现代科学分支。如此复杂而精细的生物智慧是如果发展而来的呢?目前
这个问题
还没有公认的答案,不过它的最终答案需要高度回归到数学和物理这些基础学科。
小编相信,
再复杂的现象也可以用简单的常识来描述,
正好像再茂盛的参天巨木也有根一样
。
最后欢迎读者们的意见和建议,也欢迎各种形式的讨论
(可关注小编的公众号“科普最前线”,内附小编联系方式)
。
参考文献:
[1] http://www.wpro.who.int/china/mediacentre/releases/2016/20160406/en/.
[2] Laurie Kelly McCorry,
Essentials of Human Physiology for Pharmacy
, CRC Press, 2004.
[3] http://www.webmd.com/diabetes/tc/diabetes-differences-between-type-1-and-2-topic-overview.
[4]
James
Keener and
James
Sneyd,
Mathematical Physiology
,
Interdisciplinary Applied Mathematics, Springer 2008.
[5] https://people.math.osu.edu/yang.2677/Files/codes/beta.ode.
[6] https://people.math.osu.edu/yang.2677/Files/codes/betaAni.ani.
[7]
大数据时代,参数怎么降维?
[8]
混沌理论到底是什么——从蝴蝶效应出发
[9] C. S. Nunemaker et. al,
Glucose modulates Ca2+ oscillations in pancreatic islets via ionic and glycolytic mechanisms
,
Biophysical Journal(
生物物理期刊,隶属《细胞》旗下) , 2006.
[10] Ahmad R. Sedaghat, Arthur Sherman, Michael J. Quon,
A mathematical model of metabolic insulin signaling pathways
, AJP-Endo(
美国生理学期刊-内分泌与代谢子刊
), 2001.
[11] http://mp.weixin.qq.com/s/_LV0TtN-EXKK5zMXlUz84g.
本文经授权转载自微信公众号
科普最前线
更多精彩请进入下方传送门

编辑:山寺小沙弥
近期热门文章Top10
↓ 点击标题即可查看 ↓
1.
数学系和物理系的学生有什么差别?
2.
近85%的跑步者因跑步而受伤,你进行的慢跑真的对身体有好处吗?| SciFM Vol.08
3.
西瓜必须死,就在这个夏天
4.
再次颠覆认知!看完这些图,你才真正知道人类有多么渺小
5.
爱因斯坦曾经认为不可能的事情,天文学家刚刚做到了
6.
这又是一篇十分正经的招生宣传,不过聊的是国科大……
7.
超算界祁同伟,谷歌要让全世界向量子霸权低头
8.
描述混乱程度的物理量?熵究竟是个什么鬼?
9.
孩子,有时候并不是生活欺骗了你,而是你可能还不懂概率统计……
10.
科学史上最伟大的十位单身男科学家
点此查看以往全部热门文章






