做极品投资,与伟大的企业家同行,向伟大的时代致敬!
来源/孤独大脑(ID:lonelybrain)
整个宇宙可以看作一台计算机——一台巨大的信息处理机器。
上
让我们从一道有趣的题开始:
国王有一百桶酒,比自己的生命还重要。结果有一天其中一桶被投了慢性毒药,喝了以后半个小时就会死掉。国王大怒,命令玩忽职守的侍卫去试毒。酒不能被混合,一个侍卫可以喝多桶酒,一桶酒也可以由多个侍卫喝。
请问:
怎么样才能用最少的侍卫、在半小时内知道哪桶是毒酒?
解法1:一维法
最简单的方案,是让每个人试一桶酒,用时30分钟,就可以判断出哪一桶酒有毒。
这个是“一维”的直线思维,在现实生活中也未尝不可,好过什么都不干。
这样的解法,答案是:
99个人
。
解法2:二维法
从二维层面去思考,引入笛卡尔的坐标。
把100桶酒摆成10✖️10的矩阵,如下:
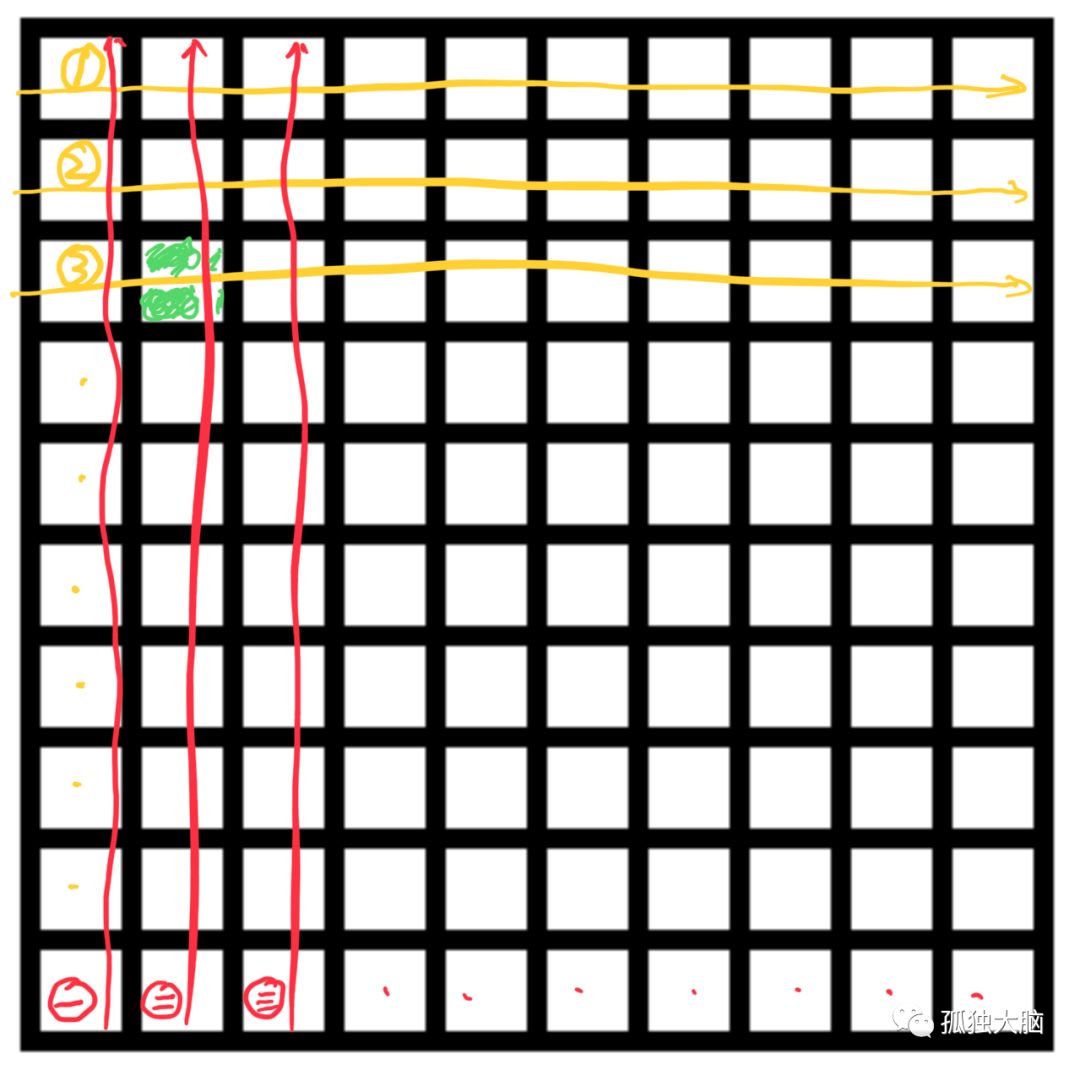
接下来:
-
让阿拉伯数字编号的1号侍卫(如上图,黄色),把第1行酒每桶喝一口,一直到10号喝第10行;
-
让汉字编号的一号侍卫,把第一列酒每桶喝一口,一直到十号喝第十列;
-
由于坐标的定位功能,假如毒酒在图中绿色的位置,那么3号侍卫和二号侍卫都会死,自然可以锁定毒酒的位置。
这样的解法,答案是:
20个人
。
解法3:三维法
能否再延伸至三维层面去思考呢?
我们很容易想到,搭建一个5✖️5✖️4的三维模型,正好有100个位置放酒,如下:
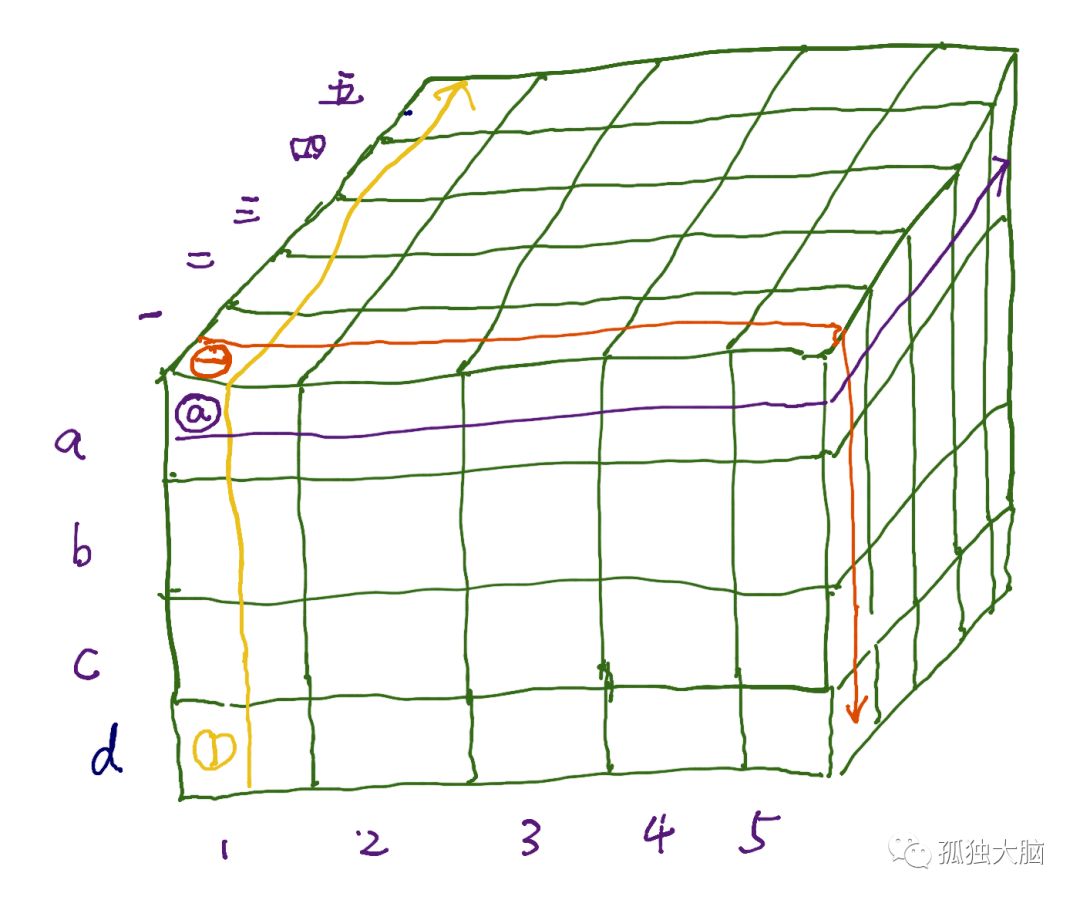
接下来(和二维解法差不多):
-
让阿拉伯数字编号的1号侍卫(如上图,黄色),把黄色箭头这一面墙的酒每桶喝一口,一直到5号喝第5面墙;
-
让汉字编号的一号侍卫(如上图,橙色),把橙
色箭头这一面墙的酒每桶喝一口,一直到五号喝第五面墙
;
-
让字母编号的a号侍卫(如上图,蓝色),把蓝
色箭头这一层的酒每桶喝一口,一直到d号喝第四层
;
-
同理,通过三个维度,也可以锁定毒酒的位置。
这样的解法,答案是:
14个人
。
(稍微扯一下,最笨的方法1,会死一个侍卫;方法2会死两个,方法3会死三个,总之一个维度会死一个。所以题目中有含糊的地方,到底是用最少的侍卫,还是死最少的侍卫?考虑到国王的残酷,我们姑且认为是前者。)
然而,即使聪明如你想明白了上面三个维度的解法,还是没有找到最优答案。
解法4:二进制
如果用计算机的思维来分析这个问题,那么首先考虑如何存储这100桶酒。100桶酒可以用二进制7个bit来表示(2的7次方>100)。
上面的解法1到解法3,都是用100个位置存储100桶酒,只是描述位置的坐标,从一维到三维,效率越来越高,所以用的侍卫越来越少。
如果用二进制呢?
二进制,是逢二进一的计数编码方法,只有0和1两个数码。那到了2怎么办?只有往前进一位,变成10。
所以,十进制的2、3、4、5,二进制分别表示为10、11、100、101。二进制广泛应用于电子计算机的数据处理。
二进制数字是信息的最小单位,又称为“比特”。
回到我们的题目,计算如下:
第一步
:
对于每一桶酒的二进制表示,
编码后,最长的数
字是7位数,不足七位前面用0表示
;
1号桶是0000001,
2号桶是0000010,
3号桶是0000011,
4号桶是0000100,
……
10
0号桶是1100100;
第二步
:
可以找七个侍卫,从左到右,编号“一”至“七”,每人对应一个位数,从第一位到第七位。
第三步
:
负责第一位数的侍卫“一”,只要这100桶
酒
中,二进制编码的该位数对应的数字是1,则喝掉此桶酒。
如此类推,每个侍卫喝掉他所负责的位数上数字是1的酒。
第四步
:
30分钟后,侍卫按照
“一”至“七”
,死掉的置为1,活着的置为0。
例如,假如第七桶酒为毒酒,其二进制编码是
0000111。那么按照上面的喝酒规则,其五、六、七位都是“1”,所以编号
五、六、七的侍卫都会死。
二进制的0和1,正好对应了死和活。
这样的解法,答案是:
7个人
。
下
用这个有趣的题目作为“隐喻”,来描述二进制的算法,对现实世界的“降维打击”,也许不算过分。我们不必深究何谓“降维”,姑且以“使用更少的侍卫找出准确答案”为衡量标准。
《信息简史》里提及,图灵把计算定义为
一个机械的过程,一种算法
。
人类在解决问题时常常会借助直觉、想象或灵光一闪——这些乍看上去可以说是非机械的计算,但深究起来或许又只是步骤被隐藏起来的机械计算罢了。
图灵需要把这些只可意会不可言传的东西去除。
因此,他问了一个直截了当的问题:要是机器,它会怎样做?“根据我的定义,如果一个数的小数表达式可以被机器写出来,那么它就是可计算的。”
图灵将自己想象成一台计算机,把指令编码成数,将十进制数编码成 0和 1。
他关注自己思维过程中一步步的逻辑,并将这些心智过程加以提炼萃取,得出其最小的组分,也就是信息处理的原子。














