“当我见到上帝后,我一定要问他两个问题——
什么是相对论,什么是湍流
( turbulence ) 。我相信他只对第一个问题应该有了答案”,据传,著名理论物理学家沃纳·海森堡临终前曾说过这句话。
而著名科
学家理查德·费曼也
曾将湍流称为“
经典物理学中最后一个尚未解决的重要问题
”。
由此我们也能感受出,湍流在物理学中的存在感有多大。
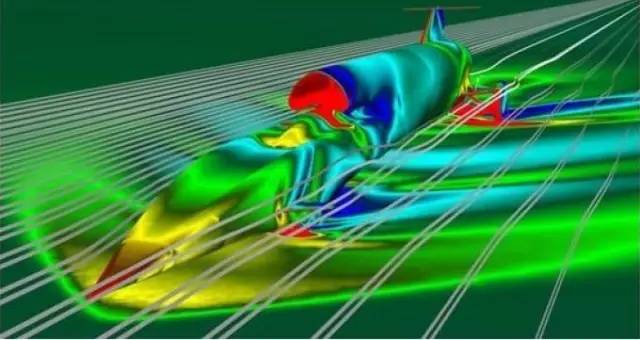
近日,一个科研团队通过模拟实验解决了湍流长期存在的一个难题:
能量是如何在湍流中运动并消耗掉的
。该研究小组由西班牙马德里理工大学航空工程师 José Cardesa 领衔,成果发表在 8 月 17 日的《科学》杂志上。

图丨费曼对湍流的评价:“最后,有一个物理问题在许多领域都很常见,它很古老,但却还没有得到解决。它不是关于寻找新的基本粒子的问题,而是一百多年前遗留下来的东西。尽管在科学上这个问题很重要,但物理领域还没人能够对其给出令人满意数学分析。这个问题就是对于湍流的解析。”
湍流本身也是一种流体动能消散的方式,即便在零粘度的情况下都会发生。而
湍流现象在我们的生活中也随处可见,比如河流绕过石头,混入牛奶中的咖啡,以及徐徐上升的青烟。简单形象地说,湍流就是大漩涡流中含有小漩涡流,但从各个尺度上看,它是一种
时间上无序但统计上又存在一定规律的运动
。

湍流的存在使得原本规则的世界变得混沌,而湍流本身的能量流动规律也异常神秘
。而最早注意到流体运动中湍流现象的是英国科学家雷诺(Reynolds)。
1883 年,他通过实验研究展示了液体在流动中存在两种内部结构完全不同的流态:
层流和湍流
。当流体流速较小时,流体质点只沿流动方向作一维的运动,与其周围的流体间无宏观的混合,即流动是分层的,也称之为层流,而当流速增大到某个值后,流体质点除流动方向上的运动外,还有向其它方向的随机的运动,这种流体形态称为湍流。层流发展成湍流的过程中,
都是从一开始的有序流体 (气体、液体) 慢慢分裂为许多
看似不可预知的漩涡
。
1922 年, L.F. Richardson 发现了湍流动能级串 ( cascade ) 过程,即
湍流在不同尺度间存在逐级能量传递,由大漩涡传递给小漩涡
。而这一过程被 Richardson 以诗歌般娓娓道来:
Big whirls have little whirls
that feed on their velocity
and little whirls have lesser whirls
and so on to viscosity
大漩涡育小漩涡以动能,
小漩涡亦以此孕子女,
生生世世以之更迭,
终消于粘滞。
不过, Richardson 的诗只说出了湍流故事的一小部分。大约 200 年前,纳维-斯托克斯方程 ( the Navier–Stokes equations ) 就已对流体的物理进行了理论的描述。
但是这一方程一般很难求出精确解
,所以工程师和科学家通常采用一些简化的理论模型或者求助于数值模拟的方法来预测流体的运动。
在过去的 12 个月,数学家们也在解释关于湍流如何耗散流体能量达到流体静止的问题上有了新的进展。而进一步理解湍流及其中的能量变化,无论是对
天体物理学家模拟星系团中的气体流动问题,还是对气候学家研究洋流问题都将大有裨益。
而在这一次的研究中, Cardesa 和他的同事宣布,他们首次成功地完全模拟了湍流中动能如何在小尺度漩涡以及更小漩涡中传递的。比如,在装满水的大水槽中,通过他们的计算模拟可以监测到,
在 1 分钟左右的时间内,能量是如何从直径为 1 米的漩涡输运到许多直径为 12 厘米的小漩涡中的
。
在实验过程中,研究人员采用了
直接数值求解
的方法,通过解不可压缩流体的纳维-斯托克斯方程对在三维周期立方体中的各项同性的湍流进行模拟,该研究团队研究了 4 个不同尺度的漩涡,他们间的尺度成 2 倍的关系。