论文地址：https://openreview.net/pdf?id=S1L-hCNtl
摘要：我们研究了生成对抗的训练方法来对马尔可夫链（Markov chain）的转移算子（transition operator）进行学习，目的是将其静态分布（stationary distribution）和目标数据分布相匹配。我们提出了一种新型的训练流程，以避免从静态分布中直接采样，但是仍然有能力逐渐达到目标分布。此模型可以从随机噪声开始，是无似然性的，并且能够在单步运行期间生成多个不同的样本。初步试验结果显示，当它临近其静态时，马尔可夫链可以生成高质量样本，即使是对于传统生成对抗网络相关理念中的较小结构亦是如此。
1 引言（略）
2 问题预设
设 S 为随机变量
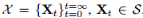的序列的状态空间。设 π0 是 X0 的初始概率分布，Tθ(·|x) 是被 θ 参数化的转移核（transition kernel），例如，使用一个神经网络。假定 Tθ 易于采样，而且对任意 θ 都有一个有效的转移核，例如，它对所有的 x ∈ S 都满足：
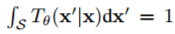
因此，在 X 的范围内每一个 Tθ都定义一个时间同质的马尔可夫链。我们把
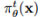表示成时间 t 下的生成概率分布。如果我们假设对所有的 xt, xt−1 ∈ S，Tθ(xt|xt−1) > 0，那么被 Tθ 所定义的马尔可夫链是不能归复（Irreducible）的，且值为正数的循环神经，因此有一个独特的静态分布
，
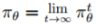且对于所有的x ∈ S，πθ满足于：
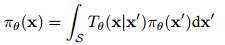
假设在我们可以得到的样本中有一个未知分布 pd(x)，比如，数据分布。我们的目的有二：找到一个 θ 使
-
πθ 接近 Pd(x)；
-
对应的马尔科夫链快速收敛。
3 马尔可夫链的对抗性训练
对于任意θ，即使πθ因为唯一的静态分布而存在，大多数情况下直接计算 x 分布的实际似然度仍然是十分困难的。然而，从
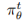获得样本却十分简单，并且如果 t 足够大，那么它将依概率收敛到πθ。这正好和 GAN 框架是一致的，即训练只需要从模型中抽样就行。
生成对抗网络（GAN）（Goodfellow et al., 2014）是采用两个参与者极小极大博弈来训练深度生成模型的框架。GAN 训练一个生成器网络 G 以转换噪声变量 z ∼ p(z) 为 G(z) 而生成样本。而辨别器网络 D(x) 则区分样本是来自生成器还是来自给定数据分布 pd 的真实样本。该关系可正式表述为以下关系式：
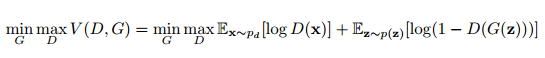
在我们的预设中，我们选择 z ∼ π 0，并令 Gθ(z) 为 t 步后的马尔可夫链状态，如果 t 足够大的话，那么 Gθ(z) 就是πθ良好的近似值。然而，我们遇到了优化方面的问题，因为需要求沿整条马尔可夫链反向传播的梯度，这就导致了梯度更新极其昂贵，即因为梯度估计量的大方差而降低的收敛速度。因此，我们提出了更加高效的近似方法，该方法可由以下目标函数表达：
