为什么MOSFET 栅极前要放一个 100 Ω 电阻？

图1中的电路所示为一个典型的高端电流检测示例。

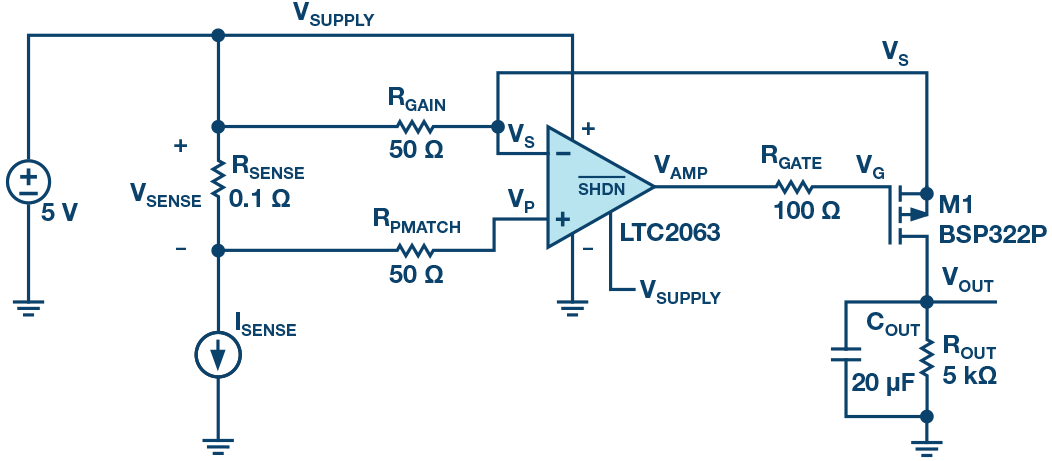图1. 高端电流检测

负反馈试图在增益电阻R _GAIN 上强制施加电压V _SENSE 。通过R _GAIN 的电流流过P沟道MOSFET (PMOS)，进入电阻R _OUT ，该电阻形成一个以地为基准的输出电压。总增益为:

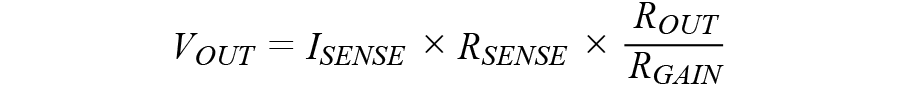
电阻R _OUT 上的可选电容 C _OUT 的作用是对输出电压滤波。即使 PMOS 的漏极电流快速跟随检测到的电流，输出电压也会展现出单极点指数轨迹。

原理图中的电阻 R _GATE 将放大器与PMOS栅极隔开。其值是多少？经验丰富的 Gureux 可能会说：“当然是100 Ω！”

我们发现，我们的朋友Neubean，也是Gureux的学生，正在认真思考这个栅极电阻。Neubean在想，如果栅极和源极之间有足够的电容，或者栅极电阻足够大，则应该可以导致稳定性问题。一旦确定R _GATE 和C _GATE 相互会产生不利影响，则可以揭开100 Ω或者任何栅极电阻值成为合理答案的原因。

图2所示为用于凸显电路行为的LTspice仿真示例。Neubean通过仿真来展现稳定性问题，他认为，稳定性问题会随着RGATE的增大而出现。毕竟，来自R _GATE 和C _GATE 的极点应该会蚕食与开环关联的相位裕量。然而，令Neubean感到惊奇的是，在时域响应中，所有R _GATE 值都未出现任何问题。

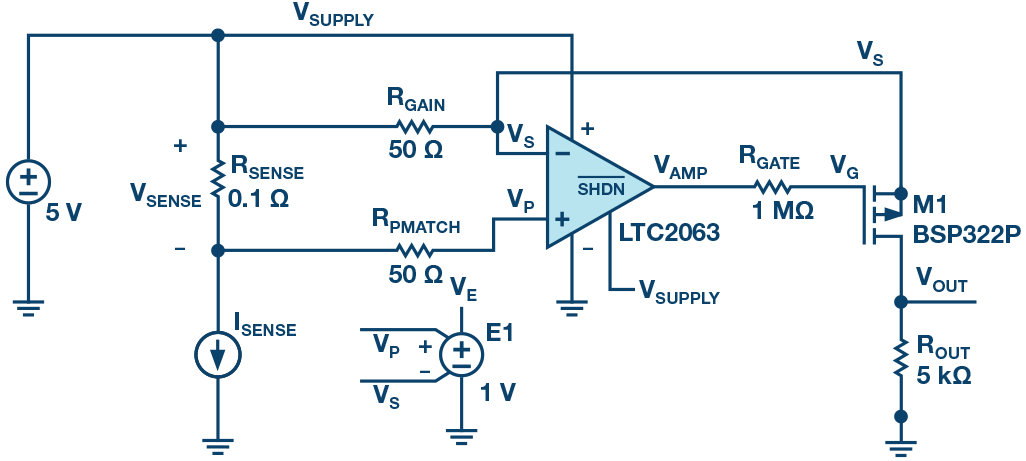
图2. 高端电流检测仿真

在研究频率响应时，Neubean意识到，需要明确什么是开环响应。如果与单位负反馈结合，构成环路的正向路径会从差值开始，结束于结果负输入端。Neubean然后模拟了V _S /(V _P – V _S )或V _S /V _E ，并将结果绘制成图。图3所示为该开环响应的频域图。在图3的波特图中，直流增益很小，并且交越时未发现相位裕量问题。事实上，从整体上看，这幅图显示非常怪异，因为交越频率小于0.001 Hz。

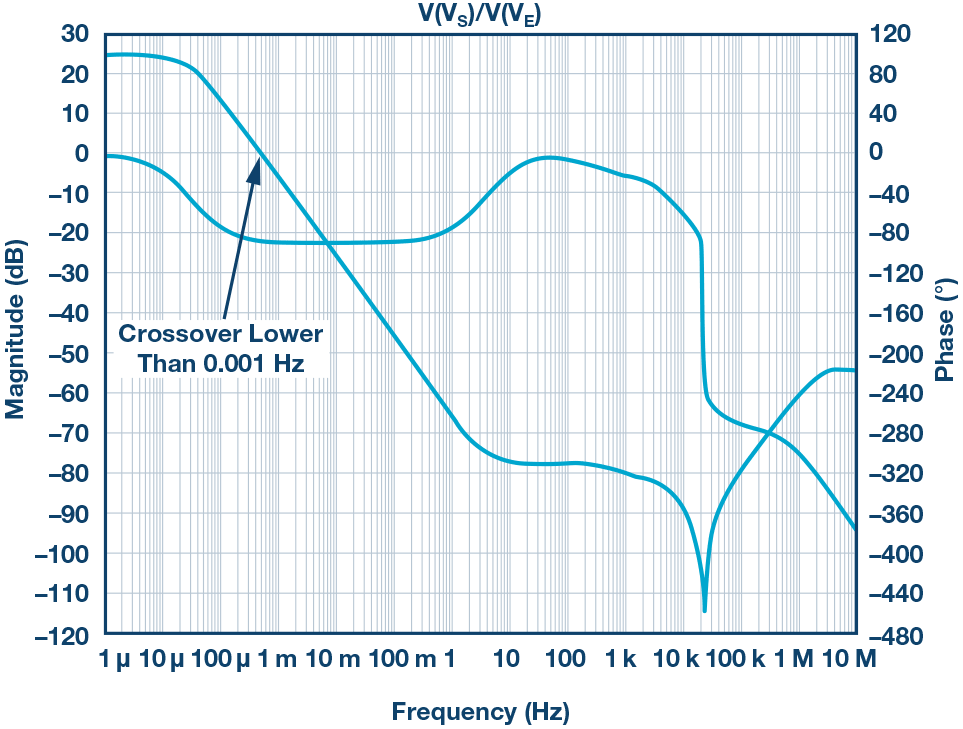
图3. 从误差电压到源电压的频率响应

将电路分解成控制系统的结果如图4所示。就像几乎所有电压反馈运算放大器一样，LTC2063具有高直流增益和单极点响应。该运算放大器放大误差信号，驱动PMOS栅极，使信号通过R _GATE – C _GATE 滤波器。C _GATE 和P _MOS 源一起连接至运算放大器的–IN输入端。R _GAIN 从该节点连接至低阻抗源。即使在图4中，可能看起来R _GATE – C _GATE 滤波器应该会导致稳定性问题，尤其是在RG _ATE 比R _GATE 大得多的情况下。毕竟，会直接影响系统R _GATE 电流的C _GATE 电压滞后于运算放大器输出变化。

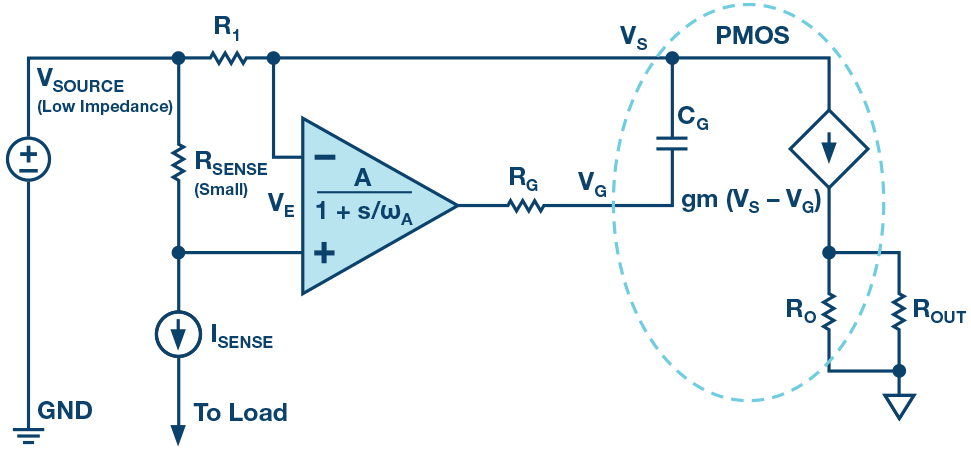
图4. 高端检测电路功能框图

对于为什么R _GATE 和C _GATE 没有导致不稳定，Neubean提供了一种解释：“栅极源为固定电压，所以，R _GATE – C _GATE 电路在这里是无关紧要的。你只需要按以下方式调整栅极和源即可。这是一个源极跟随器。”

经验更丰富的同事Gureux说：“实际上，不是这样的。只有当PMOS作为电路里的一个增益模块正常工作时，情况才是这样的。”

受此启发，Neubean思考了数学问题——要是能直接模拟PMOS源对PMOS栅极的响应，结果会怎样？换言之，V(V _S )/V(V _G )是什么？Neubean赶紧跑到白板前，写下了以下等式：

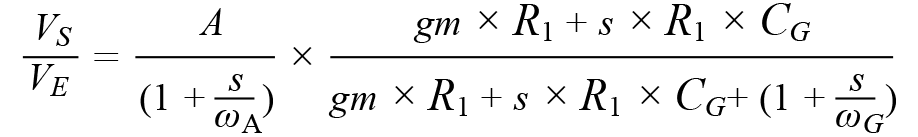
其中，

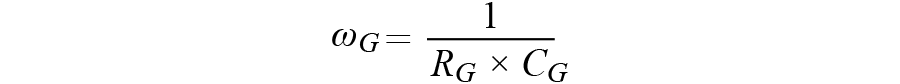
运算放大器增益为A，运算放大器极点为ωA。

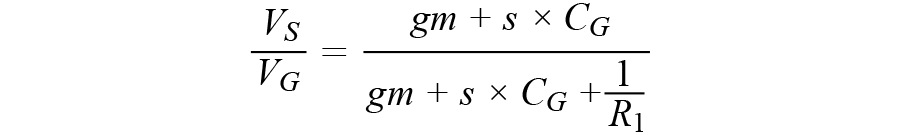
Neubean立刻就发现了重要项gm。什么是gm？对于一个MOSFET，

看着图1中的电路，Neubean心头一亮。当通过RSENSE的电流为零时，通过PMOS的电流应该为零。当电流为零时，gm为零，因为PMOS实际上是关闭的，未被使用、无偏置且无增益。当gm = 0时，V _S /V _E 为0，频率为0 Hz，V _S /V _G 为0，频率为0 Hz，所以，根本没有增益，图3中的曲线图可能是有效的。

带来这点启示，Neubean很快就用非零的I _SENSE 尝试进行了一些仿真。

图5为从V _E 到V _S 的响应增益/相位图，该曲线跨越0dB以上到0dB以下，看起来要正常得多。图5应该显示大约2 kHz时，100 Ω下有大量的PM，100 kΩ下PM较少，1 MΩ下甚至更少，但不会不稳定。

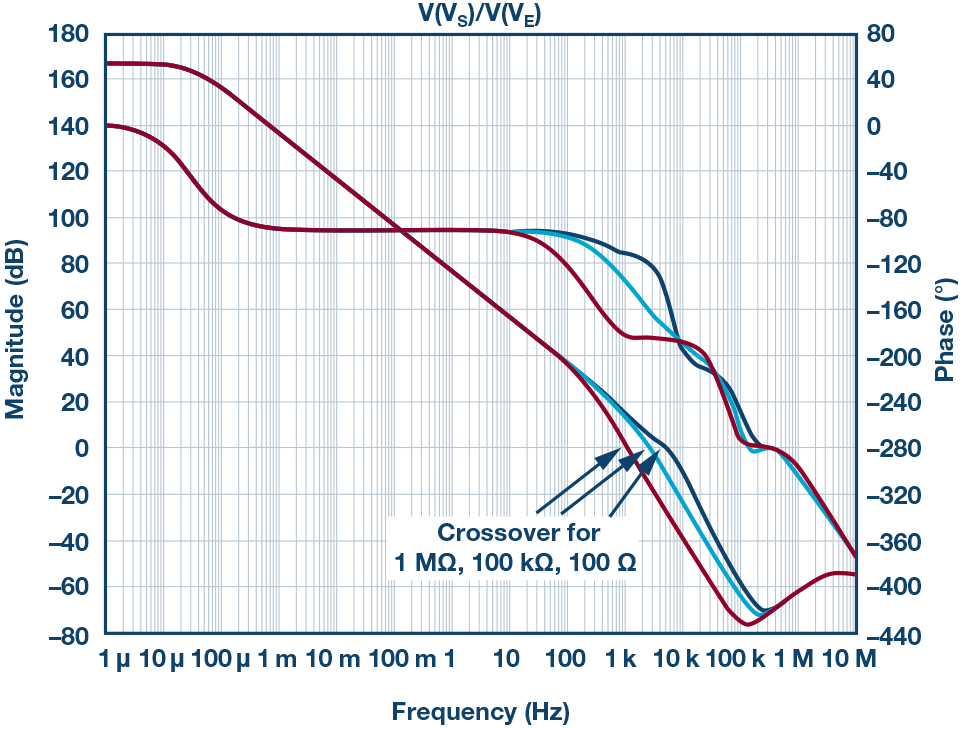
图5. 非零检测电流条件下从误差电压到源电压的频率响应

Neubean来到实验室，用高端检测电路LTC2063得到一个检测电流。他插入一个高R _GATE 值，先是100 kΩ，然后是1 MΩ，希望能看到不稳定的行为，或者至少出现某类振铃。不幸的是，他都没有看到。他尝试加大MOSFET里的漏极电流，先增加ISENSE，然后使用较小的RGAIN电阻值。结果仍然没能使电路出现不稳定问题。

他又回到了仿真，尝试用非零ISENSE测量相位裕量。即使在仿真条件下也很难，甚至不可能发现不稳定问题或者低相位裕度问题。

Neubean找到Gureux，问他为什么没能使电路变得不稳定。Gureux建议他研究一下具体的数字。Neubean已经对Gureux高深莫测的话习以为常，所以，他研究了R _GATE 和栅极总电容形成的实际极点。在100 Ω和250 pF下，极点为6.4 MHz；在100 kΩ下，极点为6.4 kHz；在1 MΩ下，极点为640 Hz。LTC2063增益带宽积(GBP)为20 kHz。当LTC2063具有增益时，闭环交越频率可能轻松下滑至R _GATE – C _GATE 极点的任何作用以下。

意识到运算放大器动态范围需要延伸至R _GATE – C _GATE 极点的范围以外，Neubean选择了一个更高增益带宽积的运放。LTC6255 5 V运算放大器可以直接加入电路，增益带宽积也比较高，为6.5 MHz。

Neubean急切地用电流、LTC6255、100 kΩ栅极电阻和300 mA检测电流进行了仿真。

然后，Neubean在仿真里添加了R _GATE 。当R _GATE 足够大时，一个额外的极点可能会使电路变得不稳定。

图6和图7显示的是在高RGATE值条件下的仿真结果。当检测电流保持300 mA不变时，仿真会出现不稳定情况。

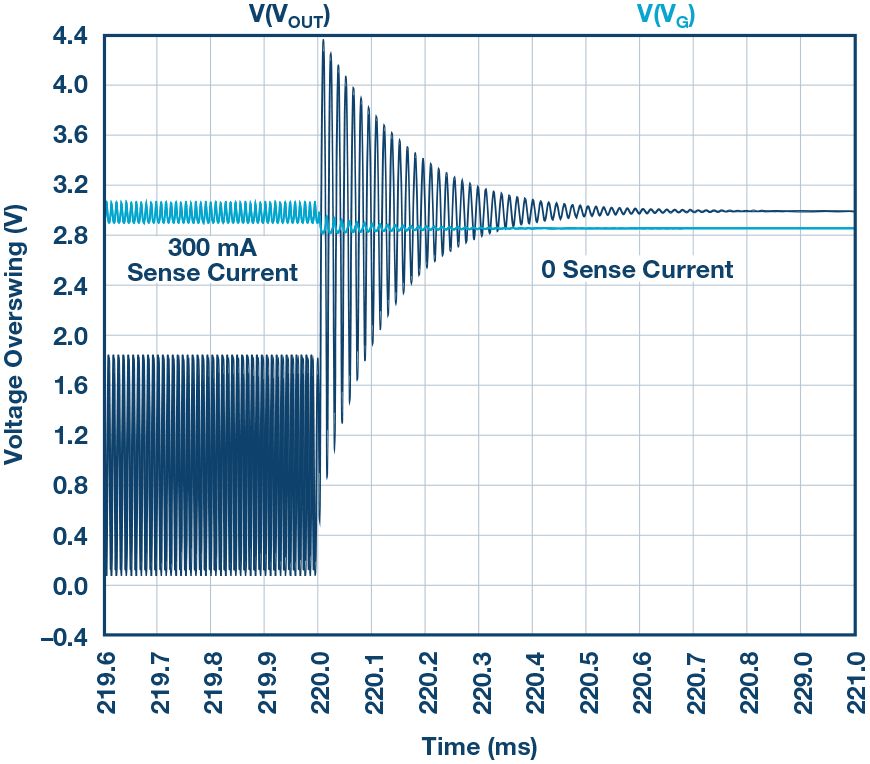
图6. 有振铃的时域图

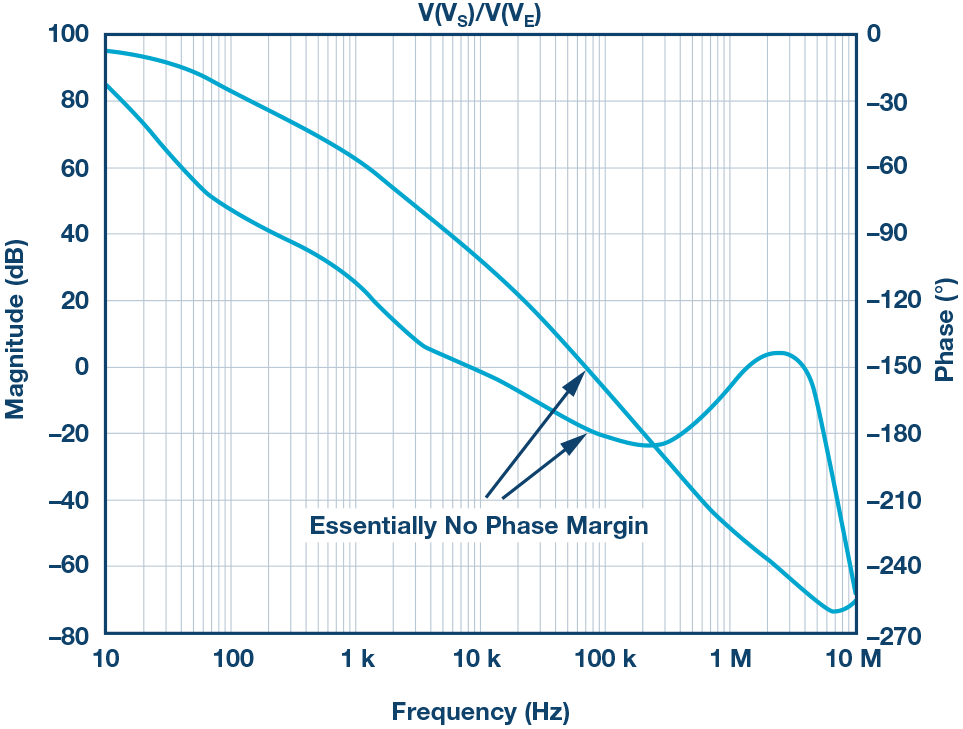
图7. 增加电流（VE至VS）后的正常波特图，相位裕量表现糟糕

为了了解电流是否会在检测非零电流时出现异常行为，Neubean用不同步进的负载电流和三个不同的R _GATE 值对LTC6255进行了测试。在瞬时开关切入更多并行负载电阻的情况下，I _SENSE 从60 mA的基数过度到较高值220 mA。这里没有零I _SENSE 测量值，因为我们已经证明，那种情况下的MOSFET增益太低。

实际上，图8最终表明，使用100 kΩ和1 MΩ电阻时，稳定性确实会受到影响。由于输出电压会受到严格滤波，所以，栅极电压就变成了振铃检测器。振铃表示相位裕量糟糕或为负值，振铃频率显示交越频率。