关于总体均值与样本均值的通用字母符号：
不知道用“字母符号”描述是否准确，暂时这么说吧。上周因为家里网络问题，导致在发送文章的时候没有把最后修改版发送出去，这里先跟大家道个歉哈。
一般情况下，总体均值用μ，标准差用σ表示，样本的均值用
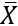表示，样本标准差用S表示。这些“字母符号”比较常用，以后本系列也会沿用这种习惯表达方法，以便大家在看其他资料时能快速反应过来。但是这不是绝对的，也有人喜欢用自己习惯的字母表示它们，所以看资料时要仔细哟。
关于CV值：
上周文结尾，有人问道量纲是什么的问题，嗯，简单地说，一个数字和一个单位一起就构成量纲，当然，具体的解释大家可以百度一下。
那么，为什么需要消除量纲呢？比如说，我想对比某地5~6周岁儿童的身高和体重两个指标，看哪个变异度大，比较变异度，那么容易想到的是方差和标准差，对吧，但是我们如果直接比较两组数据的方差或标准差，那么会出现一个问题，它们之间的量纲不同。大家回忆一下方差的公式，方差表示每个样本量与均值的差的平方之和，除以样本量，于是我们粗略认为，通过方差来看一组数据的变异程度时，这个变异量是与“均值的平方”等量纲的（均值是有单位的，且均值的单位与个体单位相同；方差，标准差也是有单位的哦，方差标准差的单位和均值的单位是什么关系？大家自己思考哈）。
好的，现在我们再比较上例身高和体重两个指标的变异度，就要分别把它们的方差处理一下，让它们的量纲都为1，应该怎么做？是不是要选用各自的标准差，再分别除以各自的均值就可以了？这就是变异系数CV的意义了。
接下来可能有人问，为啥我要比较两组量纲不同的数据呀，有啥意义呢？因为有时候我们需要比较不同量纲的数据，举个常用的例子好了：
假如我想比较A市的城镇与乡村居民中5~6周岁儿童的生长发育情况，其中身高和体重是可以反应生长发育较好的两个指标（当然这是为了方便举例随便掰的，现实生活中不会那么简单就比较单一数据的指标），我想从两个指标中挑一个，究竟用身高为f反映生长发育指标更好呢，还是用体重？这时候我们就希望作为指标的数据更为稳定，即变异度较小，于是，我们就需要比较它们之间的变异程度了，对吧？
关于离群点：
离群点是什么？离群点是我们在分析一组数据中剔除的点。比如说一批产品中抽样200个进行调查，发现有两个产品严重不合格，研究发现，这两个不合格的产品都是同一个生产线制作的，后来发现这条生产线加工的产品不合格率极高，于是这条生产先加工的产品都被撤回，重新加工，而本批次统计抽样结果时，把该生产线的产品测量数据全部剔除，这些剔除的，就是离群点。无论被剔除的数据是最大值还是最小值，已经不重要了，这些数据不参与统计分析。
再举一例，假设我们要调查正常情况下，某大学男女生上网的在线时长，发现有一个数据是：平均每天在线时长超过了12h，天哪！后了解发现，这是一位上网的瘾君子，那这位同学的情况不符合“正常情况下”这个设定，于是在统计过程中剔除出去，不作分析，这也是离群点。
所以大家明白了吗？离群点，根据研究目的，对一组数据中不感兴趣或不能反应总体情况的点予以剔除的数据。由于是否剔除数据这个决定存在这一定的主观性，因此，在作分析时，需要展示出来，并对剔除数据的原因予以解释。
通常箱式图上可以通过标记散点的方式展示离群点，但并不是箱式图上标记的所有散点就是离群点哦。有时候，作者为了让读者更直观地看到数据的分布或看到关键点在数据分布中的位置，也会在箱式图上把所有或关键数据展示出来，这时大家要擦亮眼睛，认真地看看作者的解释啦。
当然，箱式图中轴时最高最低两端一般就是最大最小值，“箱子”的顶边与底边一般是75和25百分位数，“箱子中间”较粗的横线一般就是中位线啦，这是约定俗成的，除非有特殊说明它们有别的意义吧。
关于本系列更新时间：
如无意外，本系列周一更新一期，每期几篇不定，但每期都会集中大家的问题，在下一期中有答疑环节。
关于把统计与生信结合：
由于本系列是由入门开始写，主要内容是帮助统计学小白入门，及对统计的概念的理解及应用，后面是否和生信结合很难说，有时候心血来潮或许会用R或Python尝试画图，大家心痒的话，建议先翻看生信媛的R系类文、还有强烈介绍数据挖掘系列文哦，一定会有惊喜的，哈哈！
更多内容敬请关注我们的公众号：生信媛！看，下面跑出来一个生信媛的二维码，还不快扫它！
