一直追随我们这个科学史随笔系列的读者也许会注意到一个特点,那就是在迄今为止的古希腊部分里,数学占了很大比例。
这不是偶然的,因为古希腊科学中最具持久性的成果大都是数学成果——而这本身也不是偶然的。
在现代科学哲学中,数学跟自然科学是有分别的,我们虽无意细谈这种分别,却不妨用爱因斯坦的一句话来概述。
在一次题为《几何学与经验》的演讲中,爱因斯坦曾经说道:
“只要数学命题是涉及实在的,它们就不是可靠的;
只要它们是可靠的,它们就不涉及实在”。
这句话精辟地显示出了数学的特点。
从自然科学的视角看,这种特点略悖理性:
因为早期的数学概念往往来自自然科学、来自实在。
但我们越崇尚数学的可靠性,就必须越承认它与自然科学的分别,以及与实在的距离。
在人类思想史上,直到近代仍有知名学者,比如法国哲学家勒内·笛卡尔(René Descartes),试图以纯粹思辨来研究自然科学,结果往往错得很离谱。
因为纯粹思辨最适于研究的其实是数学;
而数学与自然科学的分别,以及与实在的距离,则正是以纯粹思辨研究自然科学的最大软肋。
由于在实验科学诞生之前的年代里,纯粹思辨无可避免地是研究自然的主要手段,因此,在数学以外的领域往往错得一塌糊涂——虽然很多开风气之先的贡献依然令人景仰,最具持久性的成果则大都是数学成果。
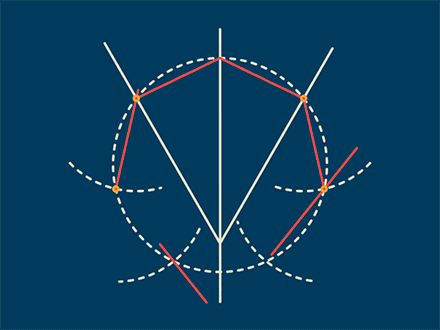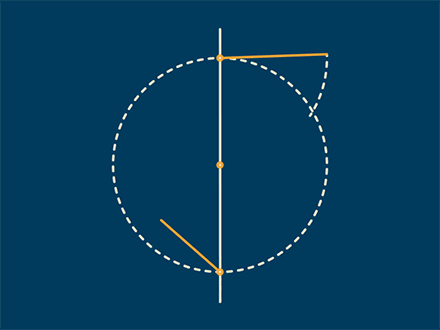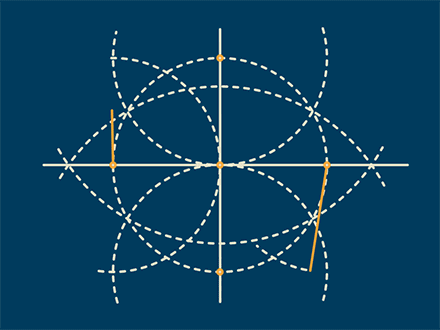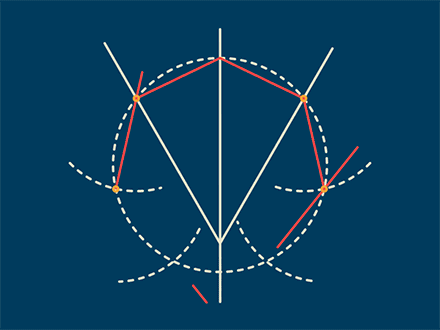
美国斯坦福大学的已故数学史学家威尔伯·诺尔(Wilbur Knorr)曾经表示,古希腊数学里的“问题”是专指作图问题。
而据数学史学家托马斯·希斯(Thomas Heath)引述的公元4世纪的希腊数学家帕普斯(Pappus)的说法,古希腊人将作图问题分为三类:
可用(不带刻度的)直尺和圆规解决的被称为“平面型”、需辅以圆锥曲线的被称为“立体型”、需辅以螺线等其他曲线的被称为“线型”。
由于数学很早就有一种追求“最简”的趋势,因此一个作图问题如果是“平面型”,人们通常就不希望用到“立体型”或“线型”里的工具,这种追求使“尺规作图”这一“平面型”的作图框架获得了特殊的重要性。
一般认为,“尺规作图”是公元前5世纪的希腊数学家恩诺皮德斯(Oenopides)提出的。
欧几里得承袭了这一框架,在《几何原本》中用两条公设(公设1和公设3)确立了“尺”和“规”的基本操作,并解决了大量的作图问题,使之更为著名。
而这一框架的著名,又使得“倍立方”“三等分角”“化圆为方”这“尺规作图三大问题”因无法纳入这一框架而从反面暴得大名。
注:
“倍立方”问题是指“作出一立方体的棱长,使得该立方体的体积是另一已知立方体的2倍”;
“三等分角”问题是指“将任意角度三等分”;
“化圆为方”问题指“作一正方形,使其面积与另一已知的圆相等”。
罗马时代的作家普鲁塔克(Plutarch)曾转述他人的回忆,将“倍立方”问题回溯到柏拉图时代。
据他记叙,有人恳请柏拉图解决一个据说来自神谕的几何问题:
使一个立方体祭坛的体积加倍,以便消弭一场瘟疫。
对几何怀有热忱的柏拉图则“狡猾”地表示,这一神谕的用意乃是让希腊人多学点几何。
不过在推介几何的同时,柏拉图对解决途径也作了提示,称这一问题的解决有赖于找到一对给定线段的两个比例中项。
这个故事因过于契合柏拉图对几何的热诚,被怀疑有可能是柏拉图学院的人自己炮制的,而“倍立方”问题或许在那之前就已有一定知名度(从而值得炮制故事)。
故事给出的将“倍立方”问题转化为寻找两个比例中项的提示,也被认为有可能并非出自柏拉图,而是比柏拉图更年长的古希腊数学家希波克拉底(Hippocrates)提出的。
不过,故事的细节虽可争议,将“倍立方”问题转化为寻找两个比例中项的提示倒是货真价实的。
因为对于长度为a和b的一对给定线段,若能找到长度为x和y的两个比例中项,即a∶x=x∶y=y∶b,则很容易证明,如果b=2a,则x=
3
√2
a正是让边长为a的立方体体积加倍所需的边长,从而可以解决“倍立方”问题。
将“倍立方”问题转化为寻找两个比例中项的提示,则被认为是将一个数学问题转化为另一个数学问题的最早例子。
不过,将一个数学问题转化为另一个数学问题只是提示了可能的解决途径,却不等于解决问题。
“倍立方”问题最早的解决之一是由比柏拉图晚了约半个世纪的古希腊几何学家梅内克缪斯(Menaechmus)给出的。
在数学史上,梅内克缪斯被认为是最早定义圆锥曲线的人,而他之所以定义圆锥曲线,据信正是为了解决“倍立方”问题。
现代解析几何来复述,梅内克缪斯对“倍立方”问题的解决用了两条抛物线:
x
2
=ay和y
2
=2ax。
不难证明,这两条抛物线除原点以外的交点的x坐标为x=
3
√2
a,正是让边长为a的立方体体积加倍所需的边长。
当然,梅内克缪斯的这一解决方法由于用到抛物线,超出了“尺规作图”的框架,按帕普斯的分类,相当于将“倍立方”问题划为了“立体型”问题。
跟“倍立方”问题相比,“三等分角”问题没什么故事,有可能只是源自与三等分线段的简单类比,或者跟构造正多边形有关——比如构造正九边形就需要三等分60°角;
“化圆为方”问题则据普鲁塔克的说法,是公元前5世纪的古希腊哲学家阿那克萨哥拉(Anaxagoras)因宣称太阳不是神而遭牢狱之灾时,在狱中为打发时光而思考的问题。
这两个跟“倍立方”齐名并且差不多古老的问题也没有难倒古希腊的先贤。
我们在这里介绍一种并非最早,却可以同时解决这两个问题的方法,这个方法恰好冠着我们先前介绍过的阿基米德的大名——即用到了所谓阿基米德螺线。
用现代极坐标来表示,阿基米德螺线指的是由方程式r=aθ所定义的平面曲线,其中a为常数。
注:
极坐标系是一种平面坐标系。
在平面上取一定点称为极点,由极点引出一条射线,称为极轴。
平面中任意一点,都可用该点与极点之间的距离即矢径,以及该点与极点之间的连线与极轴的角度即辐角这2个参数来定义。
与其他平面坐标系如直角坐标系之间能够相互转换。
利用这一定义,“三等分角”问题的解决是完全直截了当的:
假设∠ABC是需要三等分的角,取B为极坐标原点,以AB为极轴θ=0,设C为∠ABC与阿基米德螺线的交点,则利用阿基米德螺线上任意一点离原点的距离正比于角度,可以将三等分角归结为三等分距离:
即取BD=BC/3,以BD为半径的圆与阿基米德螺线的交点E所对应的极轴BE与AB的夹角∠ABE显然就是∠ABC的1/3(因为BE=BD=BC/3)。
解决“化圆为方”问题则比较微妙,需要用到阿基米德螺线的切线。
阿基米德在《论螺线》一书中证明了这样一个命题(命题18):
设P为阿基米德螺线转完一圈与水平极轴θ=0的交点,P点处的切线与垂直向下的极轴θ=3π/2的交点为T,则OT/OP=2π。
这个命题可以用现代方法来简单地证明一下:
令∠TPO=φ,则OT/OP=tanφ;
另一方面,φ乃是阿基米德螺线在P点的切线与水平极轴的夹角,用大家熟悉的直角坐标来表示的话,tanφ=Δy/Δx,其中 Δx=Δr,Δy=rΔθ,因此tanφ=rΔθ/Δr,根据阿基米德螺线的定义,又有rΔθ/Δr=rΔθ/aΔθ=r/a=θ(当然,是在Δθ→0的极限下)。
由于P为阿基米德螺线转完一圈与水平极轴的交点,因此OT/OP=tanφ=θ=2π。
有了这一结果,就不难看到,直角三角形OPT的面积是OP·OT/2=πr
2
(r为OP的长度),也就是半径为OP的圆的面积。
由此,“化圆为方”问题就变成了作一个与直角三角形OPT等面积的正方形的问题,而这是非常容易的。
当然,用阿基米德螺线解决“三等分角”和“化圆为方”问题也超出了“尺规作图”的框架,按帕普斯的分类,相当于将“三等分角”和“化圆为方”问题划为了“线型”问题。
“倍立方”“三等分角”“化圆为方”这“尺规作图三大问题”还有许多其他解决方法,就不赘述了。
那些方法有一点是共同的,就是都用到了尺规以外的工具——也就是都超出了“尺规作图”的框架。
这不是偶然而是必然的,但这种必然性直到两千多年后的19世纪才被证明。
从这个角度讲,“尺规作图三大问题”与针对第五公设的探索一样,属于数学史上拖延最久才得到解决的问题。
不过不同于后者的是,古希腊的先贤们似乎很早就意识到“尺规作图三大问题”并非“平面型”问题,也就是说不能在“尺规作图”的框架内解决,从而很早就采用了其他方法,也因此未留下太多的失败尝试。
而他们采用的所谓其他方法,比如用圆锥曲线或阿基米德螺线,在很大程度上都是为了解决“尺规作图三大问题”而提出的,这开创了数学发展的全新方向——尤其是圆锥曲线,成为了后世科学中极重要的数学元素。
古希腊的先贤们在面对不可能问题时所展示出的创造力,甚至比势如破竹时的进展更能体现他们令人高山仰止的智慧。