电路大师课系列-模拟集成电路设计第四讲:基本π网络（上）

编者按：UCLA以电路方向的研究和教学闻名于世界，Behzad Razavi教授和Asad Abidi教授更是世界闻名的电路大师。UCLA的研究生课程模拟集成电路设计（EE215A）正是由Razavi和Abidi两位大师轮流授课。我们整理了其中精华部分与大家分享:)

前情回顾：

电路大师课系列-模拟集成电路设计第一讲:绪论与线性时不变系统

电路大师课系列-模拟集成电路设计第二讲:传输函数，零极点的形成及时域响应

电路大师课系列-模拟集成电路设计第三讲:零极点与频率响应

同学们，助教哥又回来啦！这次给大家带来基本 π 网络（上）。下部会有三电容电路（采样保持放大器）。特别感谢 UCLA 研究生焦魔的翻译工作。

基本 π 网络是模拟放大器的基础，大部分放大器或者类放大器电路都有基本 π 网络的身影，新的放大器结构也是对基本 π 网络延伸和改良。所以学好基本 π 网络是非常重要的，深刻理解基本 π 网络后，阅读更复杂的放大器的文献就不是问题了。

基本 π 网络结构

基本 π 网络通过在互易 π 网络一侧添加一个压控电流源（ VCCS ）形成一个非互易网络。我们对这个 π 网络做节点分析（大家可以顺便想一下节点分析 和 Y 参数的关系）：

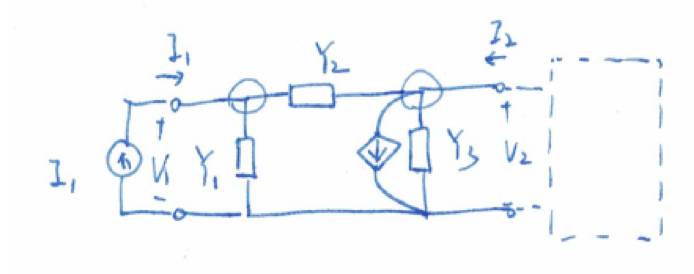
大家看，在等式右侧的受控电流移到等式左边之前， Y 矩阵还是对称的（互易）。

受控电流源移动到左侧之后，正式的 Y 矩阵就不再对称了（网络不再互易）。换句话说， VCCS 打破了这个电路的互易性。

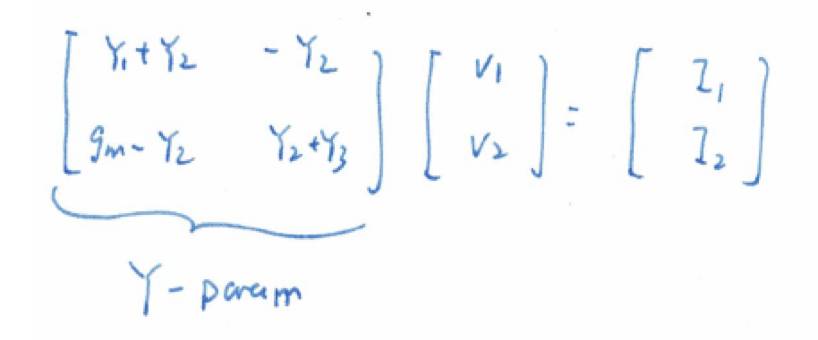
我们假设端口 2 是开路。然后可以解出这个二端口网络的一个最常用的传输函数，即跨阻。

强行解矩阵谁都会，用克莱姆法则，我们可以算出 V ₂ /I ₁ ：

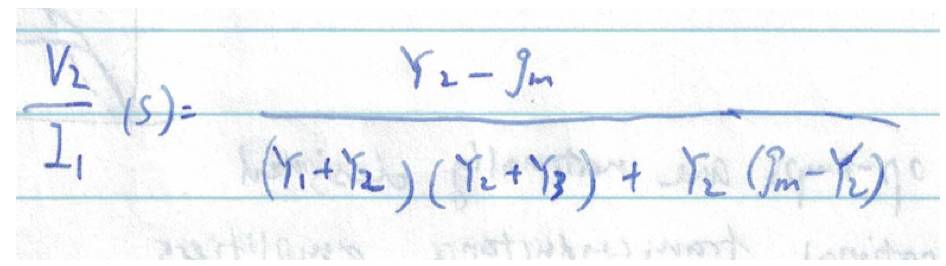
看这个公式，我们肯定会这样：

因为这个表达式是高熵的，对设计不友好的。

Prof. Abidi 教育我们，要把传输函数写成规整的、对设计友好的形式，这样才不会成为划水的电路设计师：

这三种公式都是低熵的，因为他们遵循了一个基本型：

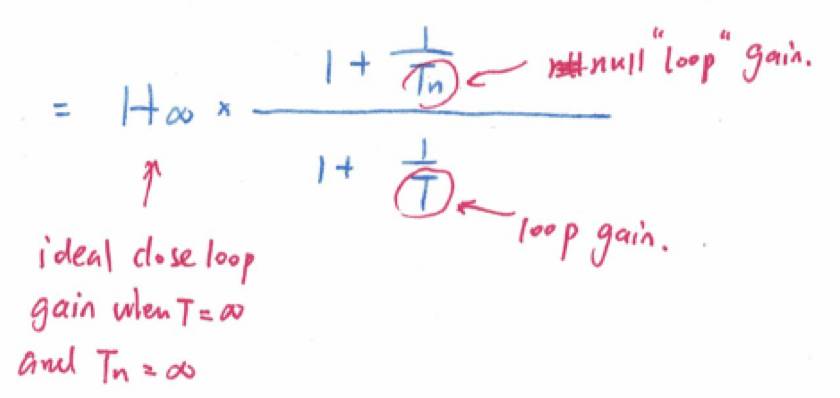
这个基本型是 Prof. Abidi 原引 Prof. Middlebrook 的广义反馈定理（ General Feedback Theorem ），以后有机会我可以专门讲 Middlebrook 的双重抵消注入（ Null Double Injection ）和广义反馈定理。这里先简单介绍一下上面的这个基本型。

H _∞ 是理想闭环增益，它可以有单位，当有单位时，“增益”这个词不再准确，但是大家心里明白就行。

T 是回路增益，它不可以有单位。 T 与这个网络反馈的能力相关。

T _n 是 Null 回路增益， 它也不可以有单位。 T _n 与这个网络的前馈的能力相关。

想要达到理想闭环增益， T 和 T _n 都必须远大于 1 才行。

用基本 π 网络分析实际电路

基本 π 网络在很多地方都有应用：

例 1 ：电阻负载跨导放大器（ OTA ）

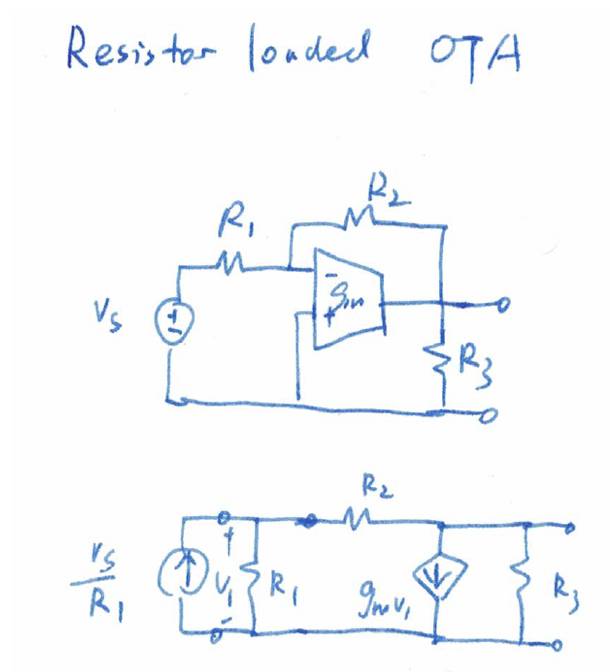
用基本型分析电路，算出增益为：

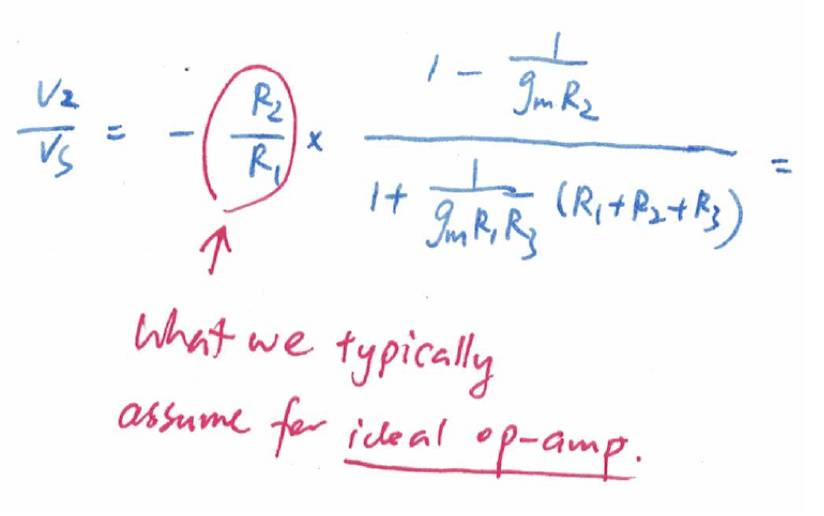
大家看， -R ₂ /R ₁ 是我们通常会假设一个理想运放接反馈电阻会有的增益。但是，要想用 OTA 达到同样的理想增益，我们需要

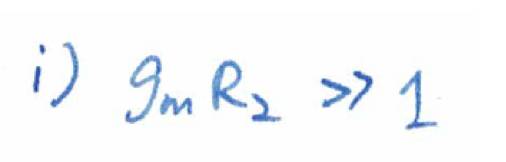
然后重写增益函数的分母， 我们可以得到：

所以还要：

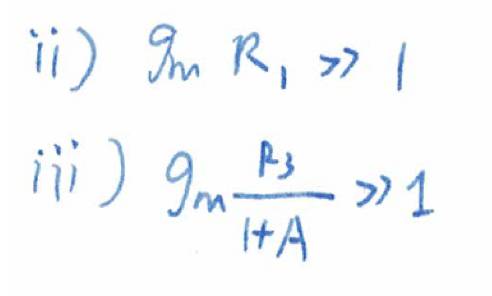
这里 A 是理想增益幅度 R ₂ /R ₁

满足了这三点，我们才能有理想的增益。这说明，如果源阻抗比较小，那 g _m 就会要很大，导致更高的功耗。满足了第二点，第一点一般都可以满足，因为需要增益的话 R ₂ 一般比 R ₁ 要大。但是第三点要求我们的负载阻抗不能太小，因为它要除以一个增益乘以 g _m 后还要远大于 1 。

例 2 ：光电信号放大器

下图展示了一个简单的光电信号放大器，该电路用于测量光电二极管输出的电流信号并转换为电压输出。

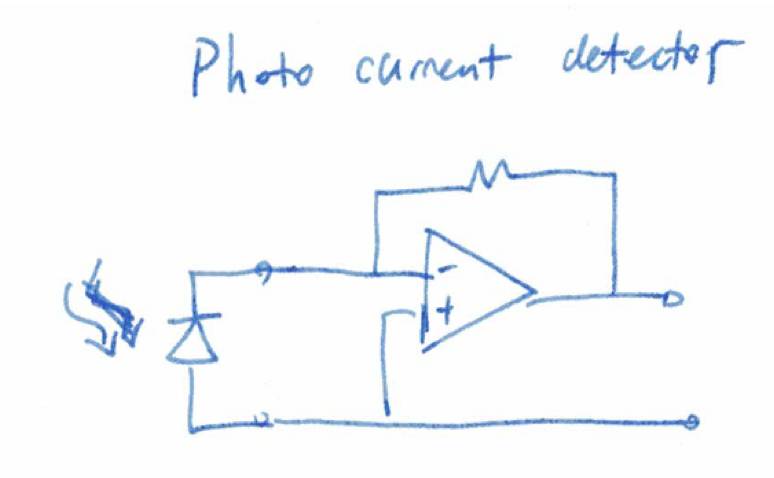
该电路的等效模型如下， C ₁ 主要为光电二极管的电容， C ₃ 为 VCCS 的寄生电容和负载电容（下一级的输入电容）。我们可以猜测 C ₃ 的一半是实现 g _m 时产生的寄生电容一半是负载电容。因为要捕捉微弱的光线，光电二极管一般很大，所以 C ₁ 可以被假设远大于 C ₃ 。 R ₂ 为反馈电阻。

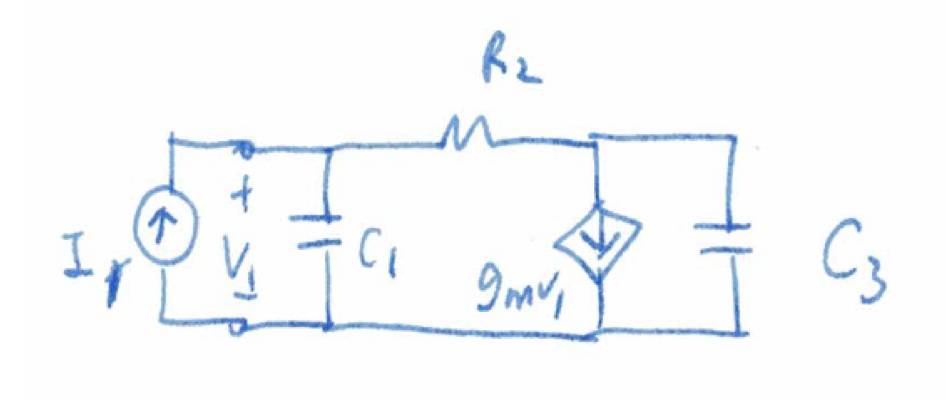
现在根据基本 π 型列出传输函数，并重写成二阶低通基本型：

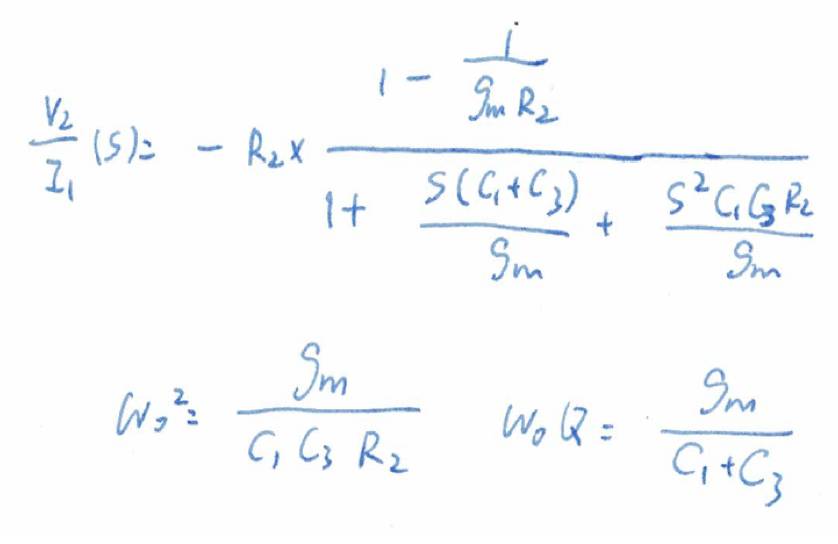
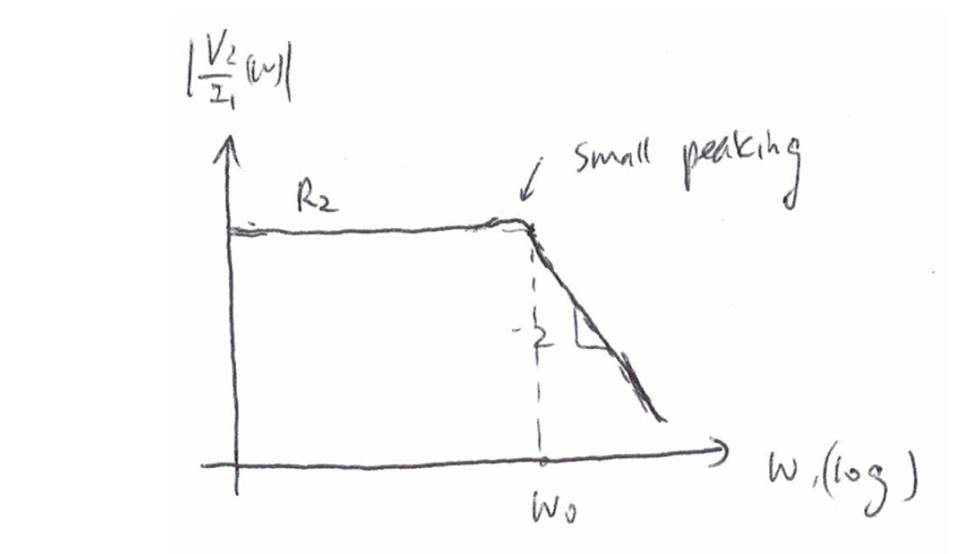
光电信号是基带信号，带宽很高 ，所以我们放大器的 -3dB 带宽要达到信号的带宽。 所以我们要让 Q 等于 1 ，这样带宽约为 ω ₀ ，而且尖峰非常小（阶跃响应不会有波纹）。

我们又知道 C ₃ 远小于 C ₁ 。所以

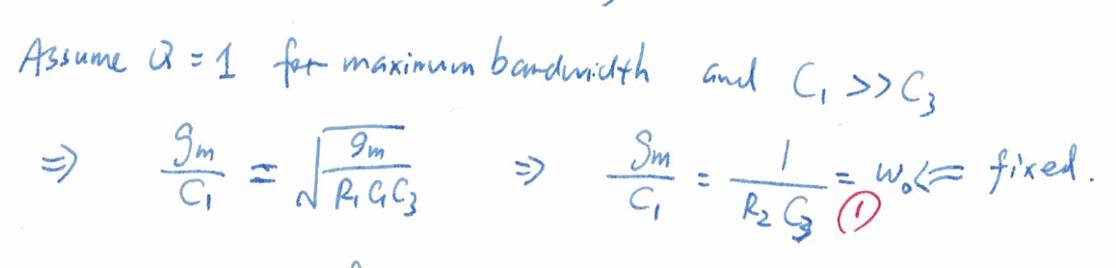
如果设计满足公式 1 ，那么 g _m R ₂ 也就远大于 1 了，因为 C ₁ /C ₃ 远大于 1 。

ω ₀ 根据信号带宽已经定下， R ₂ 根据光电二极管电流大小和目标输出幅度可以定下， C ₁ 根据发光二极管的尺寸已经定下，所以我们只需要选择 g _m 和 C ₃ 。 之后我们会学习 MOSFET 结构，但是现在我们可以做一个简单的预习设计。根据 ω ₀ 和 C ₁ 我们可以算出 g _m ，在我们所假设的一种特定条件下， g _m 正比于 W/L 。然后，根据 ω ₀ 和 R ₂ 我们可以算出 C ₃ ， 它正比于 W × L 。知道了 W/L 和 W × L 我们就可以算出 W 和 L 了，如果算出的 L 小于你所用工艺的 L ，那么这个结构就不能满足你的需求啦，要么换一个结构要么换更好的工艺吧！

最后做出来的传输函数应该长这样：

最后说一点很重要，任何手算的设计数据都是估计值，用仿真机跑出来后肯定有比较大的误差，但是没关系，我们可以降低估算的尺度，再设计几次，或者用仿真机微调。但是不管做任何设计，盲目地使用仿真机都是错误的，从手算开始的习惯是非常重要的。

最后，能看到这里的都是真爱粉，爱他的话请点文末的“赞赏”给助教哥输送核桃补脑吧

大家好，感谢大家长期以来对矽说的关注！

《矽说》创办的宗旨就是与大家分享有用的信息，倾听大家的声音，并争取帮工程师发声，为中国的芯片行业工程师社区建设尽自己的一份力量。

我们建立了矽说交流群，希望能给大家提供一个互相交流的平台，多多结识志同道合的人。也欢迎大家给我们提意见，吐槽！