生活中的密码学

一、经典密码学

每个人都有自己的秘密，这个秘密可能是美好的回忆，如第一个暗恋的女孩，也可能是尴尬的事故，如第一次尿裤子、第一次逃课。更多的时候，你的秘密是验证你身份的一种标识，比如银行卡密码、手机和电脑密码、 qq 密码。

有了秘密，就需要保存，你可以记在心里、写在纸上、记在电脑或手机等设备上。

对于记录在案的秘密，我们需要防止被其他人发现。比如假设你是一个高中男生，你给女朋友写了封情书，不希望让父母知道，那该怎么办呢？你可以选择把情书锁好，不让父母接触到。这个方法当然好，但是道高一尺、莫高一仗，小孩子总是斗不过大人的。

另一种更加有意思的办法是，你在文字上做点手脚，方法是这样的：

• 你需要给女朋友发送 Ilove marin

• 你和女朋友约定，将每个字母替换成 ascii 字母表后面的第 2 个字符

根据 ascii 代码表和映射规则， I love marin 会变成 K"nqxg"octkp ，这个一般人很难看懂，足够骗过父母了。

映射规则表：

原值	映射值	原值	映射值
I	K	m	o
空格	"	a	c
l	n	r	t
o	q	i	k
v	x	n	p
e	g

• 女朋友收到上述 K"nqxg"octkp 后，再反向把原文翻译出来，这就不是很难了。

上面我们展示的这个过程，就是一种“加密”。在我们看的谍战电视剧中，后方指挥部给前方的“谍报”人员发送命令时，使用一个密码本，将发送的信息经过映射后编程密文传送给前方，前方人员使用同样的密码本进行翻译。这与我们演示的过程如出一辙。

二、“对称”加密算法

上面的这种经典的“加密”过程，称为“对称”加密算法。假设原文为 Plain ，密文为 Cipher ，密码本为 PrivateKey ，加密过程可描述为：

Cipher= CryptoFunc （ PrivateKey, Cipher ）

这里面可以调整的是两个东西：

（ 1 ） PrivateKey ，就是谍战片中的密码本，或者“情书”例子中映射表。

（ 2 ） CryptoFunc ，这两个例子都是用了字典映射的方法。

在手工处理的场景下，上述加密和解密方法还是比较安全的，只要你没有拿到密码本，就只能靠不停的尝试来破解。

计算机诞生后，情况就不同了。《美丽心灵》里面，图灵使用了计算机辅助，帮助英国破解了德国的通信密码，在战争中起到了重要作用。现代计算机产生以后，密码学的体系得到了蓬勃发展。目前使用的“对称”加密算法，包括 DES 、 3DES 、 AES 等，加密方法都是公开的，但只要密钥长度足够，就无法暴力破解。

“对称”加密算法的原理，可以在网上很容易找到，这里就不叙述了。

二、“非对称”加密算法

“对称”加密算法的用途很大，但也有一个明显的限制，就是通信的双方必须要先协商一个共同认可的“密钥”，这在很多实际场合是做不到的，例如：

一家银行需要在互联网上提供加密通信服务，但它无法与所有的客户提前约定一个加密通信的秘钥，有下面几个原因：

• 不能所有用户共享一个 秘钥 ，这个 秘钥 迟早被泄露

• 即使每个用户单独设置一个 秘钥 ，用户也可能遗失，操作很复杂

对于这家银行来说，它需要的是这样一种机制：

• 我有一对密钥，分别是公钥 c 和私钥 d

• 所有客户都可以获取我的公钥 c ，但私钥 d 只有我自己保存

• 客户需要发送信息 x ，使用公钥进行加密，得到 c(x)

• c(x) 可以以任意的方式传送给银行

• 银行使用私钥 d ，对 c(x) 进行解密得到原文 x ， d(c(x)) = x

• 只有使用 d 才能解密，所以 c(x) 即使被其他人截获，也无法破解

在这种机制下，这家银行就不用和客户提前协商密钥了，它只要向客户公开自己的公钥，就可以实现和客户之间的保密通信。

这么牛的“加密”机制，就是我们今天广泛使用的“非对称”加密体系，也被称为“公钥私钥”体系。

但怎么才能做到呢？几个核心的要素是

• 通过 c 加密原文后，通过 d 可以解开原文，且只能通过 d 解开原文。

• c 是公开的，需要保证通过 c ，无法推导出 d

• 无法通过穷举的方法破解 c 和 d

• 为了满足密码大量使用的要求，这样的 c 和 d 还需要足够多

要做到这一点可不容易，人类到目前为止，运用高深的数学理论，也只发现了两类的方法，用于实现“非对称”加密体系，分别是：

• 基于大质因数分解的 RSA 加密算法，目前用于数字签名、 SSL 通信等领域

• 基于椭圆曲线的 ECC 算法，有取代 RSA 的趋势，在数字货币中大量使用

RSA 加密算法

RSA 加密算法，这里不计划讨论其数学推导的过程，重点展示一下有几个核心的概念。

1 、质数有无穷多个。

这个很容易证明，如果质数只有有限个，假设是 p1 - pn ，则构造一个数 k=p1*p2*pn+1 ，这个数要么自己是个质数，要么有一个不同于 p1 - pn 的质因数。

2 、如何判断一个数 m 是质数？

只能通过不断的尝试，看看有大于 1 的整数 n 整除 m 。这个过程可以做一些优化，比如只需要尝试到 sqrt(m) ，还可以把 n 按照 6K 、 6K+1 、 6K+2 、 6K+3 、 6K+4 、 6K+5 来描述，显然当 K>0 以后，只需要看看 6K+1 和 6K+5 能不能整除 m 。写成 python 代码如下

3 、对大整数 M 做质因数分解，当 M 足够大的时候，是一件非常困难的事情。

质因数分解只能通过穷举的方式去尝试， M 比较小时，计算过程是很快的，如 6=2 × 3 。但当 M 非常大时，比如 M = p × q ， p 和 q 都是质数，且 p > 2^512, q > 2^512 ，整个分解的过程在计算上就是几乎不可能。

4 、 RSA 就是根据上述的数学原理来构建密钥。分别是：

p ， q	足够大的质数
n	大数， = p*q ， n 的位数就是加密的强度
φ (n)	大数的欧拉函数， = (p-1)*(q-1)
e	在区间 ( 1, φ (n) ) 中随机选择的一个与φ (n) 质的数，一般用 65537
d	通过φ (n) 和 e 计算出的， e*d ≡ 1 (mod φ (n))

公钥是 (n,e) ，私钥是 (n,d) 。

加密过程是： m^e ≡ c （ mod n ），这是数论上的同余操作。

解密过程是： c^d ≡ m （ mod n ），证明过程需要用到欧拉定理。

5 、 RSA 的强度就是质因数分解的强度，目前的计算机水平下，强度为 1024 位的 RSA 密钥还是无法通过计算暴力破解。

6 、一个实际操作的问题，如何产生足够大的质数 p 呢？还要保证足够随机？

基本要求就是要足够随机。要产生 n 位的质数 p ，基本的算法是：

（ 1 ）产生 n 位的（ 0 ， 1 ）随机数

（ 2 ）将首位和末位都修改成 1

（ 3 ）判断其是否为质数，如果是则结束，否则回到第一步

用 python 可以演示一下上述过程：

上述代码可以产生 56 位的大质数，如： 50539924440930437 。更大的质数，就需要用到更加优化的方法了。

7 、目前这个领域最牛逼的程序是 openssl ，使用 openssl 可以快速产生公钥和私钥。用下面的命令:

openssl genrsa -out private.key 1024

openssl rsa -text -in private.key

ECC 加密算法

这个算法用到的数学就更多了，后面再慢慢细讲,本文略过.

三、“非对称”加密算法的常见应用场景

1 、加密通信。

以 RSA 算法为例，使用公钥对报文进行加密，使用私钥解密，通信过程不怕信息泄露。从 RSA 的细节可以看出，只能对不超过 n 的整数进行加密。那如何加密一段很长的文本呢？实践中有两个方法：

（ 1 ）将文本切割成多段，每一段长度不超过 n 的位数，逐段加密后再拼接

（ 2 ）更好的方法是，采用“对称”加密和“非对称”加密结合的方法，如先选一个随机密钥，用 DES 加密算法将原文加密，然后在用 RSA 公钥，对前面使用过的 DES 密钥进行加密，和密文一起发送。接收者先用私钥解开 DES 密钥，再用 DES 密钥解开原文。 SSL 的握手协议（ https ），就是这样实现的。

2 、身份识别（数字签名）

日常生活中，签名是非常重要的。

• 在一张银行转账单上签名，代表我认可这笔业务是我同意做的，如果有一天我想反悔，银行可以拿出那张签名的单据，我就无法抵赖了。

• 在一张借条上签名，代表我承认这笔借款，以后需要偿还的，否则拿着签名的借条，就可以去法院告我了。

这些案例都说明一个问题，我们需要通过签名来声明自己的身份。在计算机的世界里，怎么能做到类似的通过签名来声明身份的功能呢？

“非对称”加密可以做到这一点。

在“非对称”加密算法中，我们前面提到的都是用公钥加密、私钥解密。这个过程中，加密者可以是任何人，但解密者只能是持有私钥的人。这个过程实现的是私密通信的过程。其实还有另外一种用法，就是使用私钥加密，公钥解密。 RSA 算法保证了只有用私钥加密，公钥才能解出来，如果解出来的文本和声明的原文一致，那就可以确定之前是用私钥加密的，是其他人无法伪造出来的。这就是所谓的数字签名。其过程如下：

• 我有一对公钥和私钥，并对外公布了公钥

• 我用私钥对一段文本进行了加密，我将原文、密文、公钥一起发布出来

• 验证者用公钥将密文解开，将得到的文本与我声明的原文比较，如果相同，则验证通过。否则验证失败。

这就是数字签名的完整过程，网上银行业务的电子签名，都是这样实现的。

这里还有一个问题，如果有人使用了另一对公钥和私钥，对同样的原文进行了加密，将原文、伪造的私钥加密的密文、伪造的公钥发布出来，对这个签名的认证也是通过的。怎么才能防范这个问题呢？

实践中采用二次签名的方式就可以了。以网上银行为例，银行会使用自己的私钥对用户的公钥进行签名，并发放给用户。在用户提交业务签名时，其必须要把公钥及银行的签名一起提交，银行会验证这个公钥的签名，成功后再验证客户的签名。

打个形象的比方，银行的签名就好比银行业务单据上的公章，客户的签名就好比是签字。银行先验证公章，确保是银行的业务单据，再验证客户的签名。

通过二次签名，就解决了客户伪造公钥和私钥提交业务报文的问题。

四、再论密码

回忆一下本文第一段的问题，我们每个人都有大量的密码需要保存和记忆，例如： 银行卡、 qq 、微信、支付宝、股票账户、微博账户 ......

账户实在是太多了，所以很多人的密码都设置为类似或者相同。

设想下面的场景：

1 、你在某网站注册了用户，输入了自己的密码（例如： 1qaz2wsx ）。

2 、网站把你的密码（ 1qaz2wsx ）明文记录在了数据库中。

3 、网站不幸被黑客攻陷，你的用户信息遭到泄露，包括你的密码。

4 、黑客用你的密码，打开了你的支付宝、微信、银行账户。。。。。。

我不是在危言耸听，这是完全可能发生的。

问题的核心是，网站记录了你的密码原文，这是 万恶之源 。

不能记录密码的原文，又要实现密码的验证，这怎么才能做到呢？

这就需要用到密码学中的单向散列算法，常用的是 MD5 、 SHA-1 和 SHA-256 。

散列算法的作用是，将一段文本（ text ）映射成一段散列值，它有几个特性：

1 、相同的文本，得到相同的 hash 值

2 、不同的文本，得到相同 hash 值的概率极低。这种情况称为碰撞。

3 、通过 hash 值，无法还原成原始的文本。（并非一一对应）

4 、文本微小的变化，会导致 hash 值发生剧烈的变化。称为雪崩效应

我们可以用 python 简单实验一下：

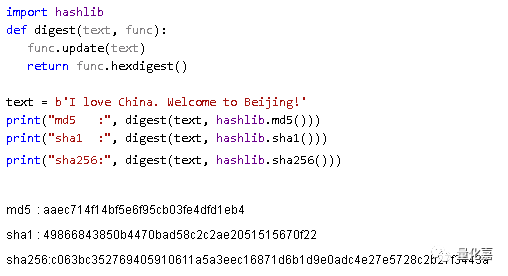
散列函数有这广泛的用途，例如：

1 、在软件分发时，同时分发软件的散列值，用户就可以验证下载数据完整性。

2 、上面网站密码的案例，系统只需要保存密码的散列值，验证时采用相同的散列方法，直接校验散列结果是否一致就可以了。

目前的状况是：

• md5 已经被认为是不安全了，改进版本是 RIPEMD160 。

• 2017 年 2 月份， google 宣布实现了 sha1 的碰撞。但目前 sha256 还没有发现漏洞，被认为是安全的。

• 比特币里面广泛使用了 sha256 和 RIPEMD160 。

至此，对身边常用的密码学的应用，做一下简单的总结，表格如下：

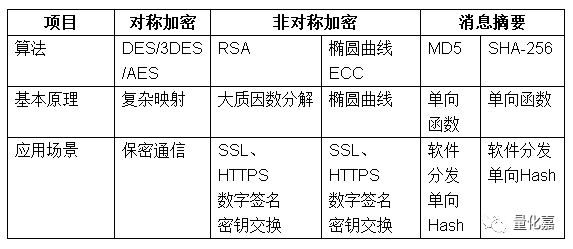
转发自 量化嘉