文/赵丽;黄文礼(本文通讯作者);巴曙松
ABSTRACT
We mainly develop a model measuring the optimal effort of a risk-neutral hedge fund manager in a continuoustime framework. The fund manager chooses the optimal effort to maximize the present value of total fees and reduce liquidation risks, trading off extra return benefits against the cost of the effort. We find that the manager's effort depends on the ratio between the fund's assets under management (AUM) and the high-water mark (HWM), and endogenous fund liquidation has key influence on the dynamics of the effort. Our calibration suggests that when the fund is close to liquidation, the manager exerts greatest effort. The more distant the fund value is from the liquidation boundary, the less effort the manager chooses to make; when the fund value is approaching the HWM, the manager's optimal effort still decreases, but the rate of decline becomes far slower. The optimal effort contributes to both increasing the likelihood of survival for the fund and preserving the fund's going-concern value. A growth of degree of the effort cost, volatility of the AUM, exogenous liquidation probability or endogenous liquidation boundary decreases the optimal effort. We also find empirical evidence that may support our theoretical conclusion.
1. Introduction
Since the 1990s, the global hedge fund industry has developed substantially and quickly, becoming increasingly important to the modern portfolio management. According to HFR inflows and performance gains through the volatile macroeconomic environment in 2015Q1 increased total hedge fund capital to a new record of $2.94 trillion. Although the hedge fund capital posted a decline in the first quarter of 2016, it still remained above $2.87 trillion. One major feature of hedge funds is the special compensation contracts. Highwater mark contracts can be regarded as the combination of option-like compensation contracts and the high-water mark (HWM), which is known as a loss carry-forward provision. Besides the management fees that are typical for mutual funds and are usually collected as 2% of the fund assets under management (AUM), i.e., the fund value, as long as the fund survives, hedge fund managers also charge performance fees. The performance fee relies on the HWM, which for each investor is the maximum value ever reached by the past fund's AUM since her investment (in some contracts, the HWM is also subject to certain adjustments). When the fund's AUM exceeds the HWM, the HWM is reset as the current fund's AUM and the manager usually receives 20% of this excess profit as a reward for good performance. In addition, the compensation contracts vary with different funds.
How is the manager's optimal effort devoted to running the fund under such compensation?
By asking this question, first, we intend to investigate the dynamics of the effort with the fund value's distance from the HWM, and discuss whether the optimal effort conduces to preserving the fund's goingconcern value. Although the HWM contracts are prevalent, whether they are optimal or beneficial is an open issue. Under the principalagent framework, Dybvig et al. (2010) discover that in a second-best world where the manager's signal about future market prices is observable but the effort is not observable, the option-like compensation contracts may be optimal. However, the research fails to describe the effort dynamics. Unlike under a management-fee compensation that is not very sensitive to the fund's performance, the manager's effort should be more dependent on the relative distance between the fund value and the HWM under the HWM contracts.
Zhan (2011) investigates and compares five compensation schemes that are commonly employed in the mutual fund or hedge fund industry, likewise under the principal-agent framework. Specially, the paper finds that the HWM provision induces more effort when the fund's AUM is slightly under the HWM, but it dampens the manager's effort when the fund's AUM is far away from the HWM and the manager's skill is poor. Ray and Chakraborty (2008) construct a simple optimization problem assuming that the portfolio follows uniform distribution, and find that as the distance between the fund's AUM and the HWM increases, the manager's effort falls.
However, both Zhan (2011) and Ray and Chakraborty (2008) only apply a single-period discrete-time model, assuming that hedge funds have a determined termination, and do not consider the possibility of fund liquidation during the limited period. In contrast, we study the dynamics of the managerial effort in a continuous-time framework of hedge fund valuation. Our setting is more reasonable in that the fund has a infinite horizon and can be liquidated once the exogenous or endogenous liquidation condition is triggered.We find that liquidation is one crucial factor that determines the effort dynamics.
Second, this question also contributes to understanding the funds' risk-adjusted extra return, α. Manager's effort plays an important role in explaining of the fund performance. Chevalier and Ellison (1999) use the average SAT score at the fund manager's undergraduate institutions as a proxy variable to reflect the manager's effort, ability or networks of contacts, and find that mutual fund managers who attended the institutions requiring higher SAT scores have better performance. Also, they recognize that younger managers exhibit better performance than those olders, and the reason is that young managers may make more effort and work harder considering that they have longer careers ahead. Similarly, for hedge funds, although market conditions, investment opportunities and leverage choices of the fund, as well as the manager's skill and luck are all determinants of the extra return α, the influence of the fund manager's own effort should not be ignored. Our findings concerning the effort can be a guide to empirical studies on hedge fund's performance.
To our knowledge, our model is the first to discuss the optimal effort of the hedge fund manager under a continuous-time framework and more practical assumptions. We extend the log-normal diffusion process setting of the AUM in Goetzmann et al. (2003) (GIR henceforth), to constant volatility σ and undetermined extra return α that the manager chooses to maximize her value function (present value of total fees). Just as GIR, throughout the paper, we assume that market opportunities, the manager's skill and the leverage are fixed, and also rule out the influence of luck on the extra return. Under these assumptions, the undecided extra return can be regarded as a measure to judge the fund manager's effort, that is, α is equivalent to the manager's effort in our model. It is a natural approach, since if the manager devotes herself to information acquisition within her capacity, she would employ a better investment strategy that results in higher excess returns on the fund. In this way, we associate the fund's extra return with the effort, and measure the manager's effort explicitly.
To increase the compensation fees, the fund manager may need to seek high extra returns through great effort. At the same time, making the effort is costly. Here we take the cost function with a form similar to that of the adjustment cost function used in Hayashi (1982) and Bolton et al. (2011). So the fund manager dynamically trades off the benefit and the cost, when deciding the optimal effort α. Our model also contains other important features of hedge funds, especially the HWM contracts and fund liquidation. When the hedge fund is liquidated, the manager will lose all future payoffs, and we will show that this costly liquidation impacts the manager's optimal effort significantly. Thanks to the fact that the risk-neutral manager's value function is homogeneous of degree one in the fund's AUM and the HWM, we find the relationship between the fund manager's effort and the ratio of the AUM and the HWM. In addition, we derive the corresponding ordinary differential equations (ODEs) for the manager's and investors' value functions, together with the lower boundary condition for liquidation and the upper boundary condition when the fund's AUM is exceeding its HWM.
In our dynamic framework, the manager's effort depends on the moneyness of the fund p, i.e., the ratio of the fund's AUM and its HWM, ranging from the lower liquidation boundary to the upper boundary, 1. The higher the moneyness p is, the lower the effort α and the decline rate. When the fund approaches liquidation, the manager tends to exert greatest effort, in spite of resulted expensive cost. The costly liquidation (downside risk) in our model damages both the manager's future payoffs and reputation. So to reduce the risk, the riskneutral manager behaves as if she was risk-averse. Also, the degree of effort decreases with the distance of the fund from liquidation. Besides, as the fund's AUM gets closer to the HWM, the manager's optimal effort still decreases, although with a slower rate, which indicates that the manager's motivation to make the fund value exceed the HWM is not strong. The payoff of performance fees shrinks the fund's AUM, increasing the probability of liquidation in the future. Our result covers the fact that a risk-neutral manager is averse to collect performance fees too soon. However, the rate of decline is becoming slower when p approaches 1, due to the coming performance fees. The optimal effort induced in our model contributes to both increasing the likelihood of fund survival and preserving the fund's going-concern value. It can be concluded that incorporating both the HWM contracts and fund liquidation is beneficial for the survival of funds and fund investors. We also find empirical evidence that may support our theoretical conclusion.
Our findings are contrast to the results in standard settings, such as Zhan (2011) and Ray and Chakraborty (2008), since the standard framework does not involve the assumption of fund liquidation, and only focuses on the HWM contracts. The HWM contracts are thought to be a series of call options on the fund value with a changing strike price, the HWM. Therefore, it is intuitive that a risk-neutral manager makes greater effort when she is close to gaining performance fees (p is approaching 1), comparing with the effort when the option-based contracts are deep out of the money. By letting the endogenous liquidation boundary be zero (with no liquidation), our model assumption is consistent with the standard settings, and the optimal effort in this case increases as p, which agrees with the standard intuition. So we claim that liquidation is one crucial risk that could determine the effort dynamics, and the increasing effort induced by the case with no liquidation is not beneficial.
We also discuss the impacts of the effort cost, market conditions and the compensation structure. An increase in the effort cost level, volatility of the AUM, exogenous liquidation probability or endogenous liquidation boundary decreases the manager's optimal effort and total payoffs to the manager. In addition, higher rate of the management fee or performance fee induces greater effort, a higher amount of total fees paid to the manager, and a lower level of investors' value. A decrease of either the management or performance fee rate has a larger impact on all the three values than an increase, and management fees play a major role in the compensation contracts.
Our findings are related to GIR, which provide a quantitative valuation framework for hedge fund dynamics for the first time. GIR derive closed-form solutions for both the manager's and investors' value functions under conditions such as the compensation structure, liquidation requirements, the HWM and investors' withdrawals. Our model also incorporates these features. Unlike their hypothesis that the net asset value follows a log-normal diffusion process, we allow a varying extra return α, which can be chosen optimally by the fund manager and represent the effort the manager is willing to make. In this way, we can investigate changes of extra returns caused by the manager's effort.
On the technical side, our paper is related to Browne (1997, 2000), which solve a series of optimal control problems concerning dynamic active portfolio management and optimal behavior of investors, respectively, with general utility functions. Following the methodology, Wang et al. (2015) study the equity-for-guarantee swap, an innovation way of enterprise financing, faced by a risk-averse entrepreneur. Li et al. (2016) construct a contract model under time-inconsistent preferences of a risk-neutral agent. Also, we consider an optimal control problem for a risk-neutral hedge fund manager. Despite the assumption of risk neutrality, the manager behaves endogenously riskaverse and makes greatest effort when liquidation risk is approaching.
Lan et al. (2013), Drechsler (2014) and PW all study the optimal leverage choice of a fund manager with different model assumptions. PW conclude that the manager acts like a Merton-type investor with a CRRA utility function, unwilling to raise the fund value over the HWM too soon. Lan et al. (2013) give a sufficient framework to analyze the economics of hedge funds, and highlight that the risk-neutral manager behaves risk-averse, and decreases leverage ratio when the fund approaches liquidation. Drechsler (2014) finds a closed-form solution to the risk choice of hedge funds, and also realizes that the degree of risk-taking lowers as the moneyness falls. In comparison, we focus on the variation of the manager's effort with fixed leverage policy. It turns out that the manager's effort increases rapidly as the fund is on the verge of liquidation, and when the AUM is close to the HWM, the effort stays at its lowest level. From the perspective of the manager's effort, the manager's risk-averse behavior near liquidation and unwillingness to prompt the fund's AUM to cross the HWM can be observed in our model simultaneously.
The remainder of the paper is constructed as follows. Section 2 presents the valuation model containing the manager's effort to be chosen optimally. In Section 3 we deduce the ODEs for value functions of both the manager and investors and determine the optimal effort. Section 4 shows some comparative statics, economic implications and empirical results. Section 5 concludes.
2.Model
The main feature of our model is the incorporation of the manager's effort as an endogenous variable to model the dynamics of hedge funds. At the same time, we also consider the adjusted HWM, management fees and performance fees, the exogenous liquidation, and performance- induced endogenous liquidation.
2.1. Compensation structure
We denote P as the fund's assets under management (AUM), i.e., the net asset value of the investors' positions, and H as the current high-water mark. Let r be the risk-free rate, and without loss of generality, we also assume that investors withdraw their positions proportional to the AUM continuously, i.e., δP, where δ represents the withdrawal rate.
The manager's payoffs come from management fees as well as performance fees. Management fees are not sensitive to the fund performance and paid continuously at a constant percentage of the AUM (denoted as c) provided that the fund survives. The payment of performance fees relies on the HWM H. In the simplest case, H is the highest historical value of the fund's AUM P. Besides that, H is also subject to certain adjustments in some compensation contracts. As in GIR, H is adjusted up at a contractually growth rate g, and down at the withdrawal rate δ, as well as the charged percentage of management fees c. The growth rate g represents the rate required by investors to compensate for their opportunity costs and the value of g can be equal to the risk-free rate r, 0, or other values depending on the contracts. When the fund's AUM P exceeds H, H is reset as the new value of P and the performance fee is paid as a fraction k of this excess profit.

2.2. Fund's AUM and manager's effort
In the absence of payouts and the probability of liquidation, the AUM P is assumed to follow a log-normal diffusion process in GIR. In the model, the expected rate of extra return and the volatility of the fund value are both constant, indicating that the impacts of stochastic market conditions and various leverage choices on the fund value are excluded from the modeling. If not, either one of these could have significant effects on the fund's returns and risks. Besides, GIR do not consider the effects of a manager's performance due to either skill or luck.
Inspired by GIR, to focus on our purposes, we also assume that the impacts of all above factors on the fund's AUM are fixed and consider a moderate-skill manager. Let αt be the extra return, or the risk-adjusted return in excess of r, and σ be the volatility of the fund's AUM, Pt.6 To analyze the optimal effort made by the fund manager, here the only varying variable (the control variable) is the extra return αt, which can be chosen by the manager to maximize her present value from all future fees. The assumption means that in our model, except for the manager's endogenous decision, other conditions make no difference to the fund's AUM. Given that the effects derived from other conditions are invariant, here the extra return αt can be regarded as a measure to represent the effort chosen by the hedge fund manager. By this means, we can evaluate the effort explicitly.
The relationship between the extra return and the manager's effort is natural. If the manager spends more time and money on searching for valuable information, finishing in-depth market analysis report, doing due diligence on products, and performing more sophisticated models to select better products and time the market within her capacity, she would construct better investment strategies and thus obtain higher extra returns on the fund. A similar relationship also exists between students' effort and their test scores. For mediocre students, their test scores are positively related to the effort they make. If they work harder, it is reasonable that the gained scores will be better.

While the manager has incentives to seek for higher extra returns so as to receive higher compensation fees, she needs to consider the accompanying cost for making certain effort, since the effort is not costless. Without loss of generality, we assume that the effort cost can be measured by a loss of wealth to the manager, and the function to measure the loss of wealth, G(αt, Pt), has a standard quadratic form, similar to the adjustment cost function in Hayashi (1982) and Bolton et al. (2011):

where i is a positive constant parameter measuring the degree of the effort cost. The convex function of the effort cost relates to both the realized effort αt and the fund value Pt, and agrees with decreasing returns to scale concerning the increased marginal effort expenditure. To choose her optimal effort, the manager needs to make a trade-off between return benefits against the effort cost while considering impacts of liquidation and the high-water mark contracts
Fund liquidation may occur for two reasons. The first one is exogenous where the liquidation is assumed to be a Poisson process with probability λ per unit of time, and such liquidation can be derived from investors' liquidity need. Let τ1 denote this exogenous liquidation time. When the exogenous liquidation occurs, the AUM Pτ1 jumps to zero, and the manager can do nothing about it. The second one depends on the fund manager's performance and is hence endogenous. If the AUM Pt drops to a substantially low level, investors would lose faith in the manager and therefore liquidate the fund. Let the level leading to liquidation be the product of a constant fraction b and the HWM H, and τ2 be this endogenous liquidation time, so that we have

In summary, the liquidation time of the fund satisfies τ = min(τ1, τ2), at which we assume that the manager loses all future fees and investors receive the fund's AUM Pτ . Prior to the endogenous liquidation, the dynamics of the AUM Pt can be deduced as follows:
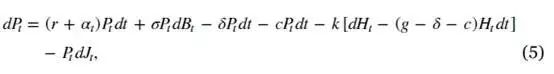
where Bt is a standard Brownian motion. The first and second terms together represent the changes of the fund value relative to the fund manager's effort. The third and forth terms reflect investors' withdrawals and management fees, respectively, and the fifth corresponds to the performance fees paid if the fund value exceeds the HWM. The last term refers to a Poisson jump process accounting for the exogenous liquidation, where Jt is a jump process with intensity λ.
2.3. Value functions
Throughout the paper, time is continuous and the hedge fund does not possess a pre-specified expiration date. The manager is risk-neutral and discounts her wealth at a constant rate β. Since the manager has the ability to pursue risk-adjusted extra returns, the time value of the manager's wealth may be more expensive and her subjective discount rate may be larger than the risk-free rate r. Following GIR, we assume that β is equal to r. Extending our model to allow for differences between the manager's subjective discount rate and the risk-free rate is straightforward, but it is not the main concern of our model and no additional insight would be obtained for our main issue. The manager's objective is to maximize her expected present value of total wealth, by choosing the optimal dynamic effort α. Let F (P, H; α) be the manager's value function, and it satisfies,
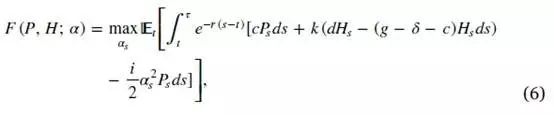
subject to the dynamics of Pt (5), the dynamics of Ht (1), the liquidation boundary condition (4) and the effort constraint (2). The manager's value function contains her payoffs from management fees and performance fees, and the loss of wealth from the cost of the effort. Upon fund liquidation, the manager loses all future payoffs, and the value function equals to 0.
Moreover, when the manager's effort is chosen, the value of investors' positions M(P, H; α) is determined as follows:
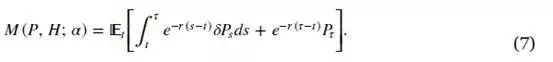
Investors's discount rate is the risk-free rate r. They receive money outflows at a fixed fraction before liquidation, and gain the whole fund value once liquidation occurs.
3.Solution
In the region P

Since the degree of the effort cost i and the AUM P in the duration of the fund are both positive, the second-order condition is naturally met.
Because the manager's optimal problem is homogeneous in the fund's AUM P and HWM H of degree one, we can apply the ratio of P and H to rewrite the above problem. Let the lowercase letters denote the corresponding variables or functions divided by the HWM H, so the variable p=P/H ranges from the liquidation boundary b to the upper boundary 1. The manager's value function can also be written as F (P, H) = Hf (P/H) = Hf (p), and in this way, the problem can be simplified from solving PDE equations to ODE ones.

Our boundary conditions follow GIR and PW. However, in our model, the fund manager influences the likelihood that the fund value hits the lower or upper boundary through the optimal effort.
Similarly, we can get the HJB equation for the investors' value function M(P, H), and through M(P, H) = Hm(p), we derive the following ODE for m(p):

(完)
文章来源:Economic Modelling 2017年4月10日(本文仅代表作者个人观点)
本篇编辑:牛淑雅
温馨提示:现微信最新版本“订阅号”已实现公众号置顶功能,广大读者可点开“金融读书会”公众号,点“置顶公众号”键,即可将“金融读书会”置顶,方便查阅。




















