
数据分析师,无疑是数据时代最耀眼的职业之一,而统计学,又是数据分析师必备的基础知识。
1.集中趋势(Central Tendency)
2.变异性(Variability)
3.归一化(Standardizing)
4.正态分布(Normal Distributions)
5.抽样分布(Sampling Distributions)
6.估计(Estimation)
7.假设检验(Hypothesis testing)
8.T检验(T-test)
一、集中趋势(Central Tendency)
1.众数
出现频率最高的数;
2.中位数
把样本值排序,分布在最中间的值;
样本总数为奇数时,中位数为第(n+1)/2个值;
样本总数为偶数时,中位数是第n/2个,第(n/2)+1个值的平均数;
3.平均数
所有数的总和除以样本数量;
小结:
现在大家接触最多的概念应该是 平均数,但有时候,平均数会因为某些极值(Outlier)的出现收到很大影响;
举个小例子,你们班有20人,大家收入差不多,19人都是5000左右,但是有1个同学创业成功了,年入1个亿,这时候统计你们班同学收入的“平均数”就是500万了,这也很好的解释了,每年各地的平均收入数据出炉,小伙伴们直呼给祖国拖后腿了,那是因为大家收入被平均了,此时,“中位数”更能合理的反映真实的情况;
二、变异性(Variability)
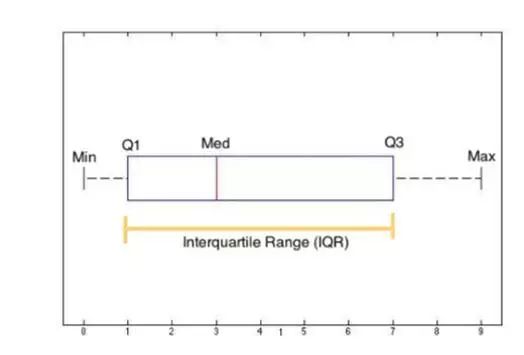
1.四分位数
上面说到了“中位数”,把样本分成了2部分,再找个这2部分各自的“中位数”,也就把样本分为了4个部分,其中1/4处的值记为Q1,2/4处的值记为Q2,3/4处的值记为Q3
2.四分位距 IQR=Q3-Q1
![]()
四分位数.jpg
3.异常值(Outlier):
小于Q1-1.5(IQR)或者大于Q3+1.5(IQR);
对于异常值,我们在处理时需要剔除;
4.方差(Variance)
![]()
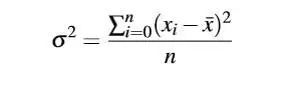
2方差variance.jpg
5.平方偏差(Standard Deviation)
-方差的算术平方根
6.贝塞尔矫正:修正样本方差
-问:为什么要用贝塞尔矫正?
实际在计算方差时,分母要用n-1,而不是样本数量n,原因如下
![]()

3贝塞尔矫正.jpg
三、归一化(Standardizing)
1.标准分数(Z-score)
一个给定分数 距离 平均数 多少个标准差?
标准分数是一种可以看出某分数在分布中相对位置的方法。
标准分数能够真实的反映一个分数距离平均数的相对标准距离。
![]()

4归一化standardizing.jpg
四、正态分布(Normal Distributions)
1.定义:
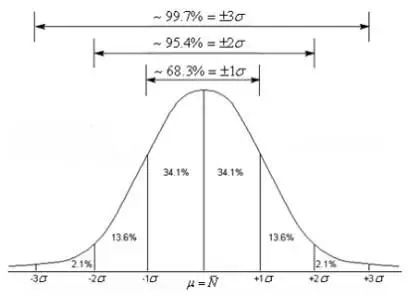
随机变量X服从一个数学期望为μ,方差为σ²的正态分布,记为N(μ,σ²)
随机取一个样本,有68.3%的概率位于距离均值μ有1个标准差σ内;
有95.4%的概率位于距离均值μ有2个标准差σ内;
有99.7%的概率位于距离均值μ有3个标准差σ内;
![]()
5正态分布normal distribution.jpg
五、抽样分布(Sampling Distributions)
1.中心极限定理(Central Limit Theorem)
设从均值为μ,方差为σ²的任意一个总体中抽取样本量为n的样本,当n充分大时,样本均值的抽样分布近似服从均值为μ、方差为σ²/n的正态分布
2.抽样分布(Sampling Distributions)
设总体共有N个元素,从中随机抽取一个容量为n的样本,在重置抽样时,共有N·n种抽法,即可以组成N·n不同的样本,在不重复抽样时,共有N·n个可能的样本。每一个样本都可以计算出一个均值,这些所有可能的抽样均值形成的分布就是样本均值的分布。但现实中不可能将所有的样本都抽取出来,因此,样本均值的概率分布实际上是一种理论分布。数理统计学的相关定理已经证明:在重置抽样时,样本均值的方差为总体方差的1/n
视频中的例子:
48盆MM豆,计算出每盆有几个蓝色的MM豆,48个数据构成了总体样本。然后随机选择五盆,计算五盆中含有蓝色MM豆的平均数,然后反复进行了50次。这就是n为5的样本均值抽样。
![]()
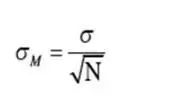
6抽样分布sampling distributions.jpg
六、估计(Estimation)
1. 误差界限(Margin of error)
![]()
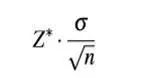
7误差界限margin of error.jpg
2. 置信度(Confidence level)
We are some % sure the true population parameter falls within a specific range
我们有百分之多少确信总体中的值落在一个特定范围内;
一般情况下,取95%的置信度就可以;
3. 置信区间(Confidence Interval)
![]()
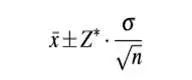
8置信区间.jpg
七、假设检验(Hypothesis testing)
![]()

9假设检验hypothesis testing.jpg
1. 问题:什么是显著性水平?
显著性水平是估计总体参数落在某一区间内,可能犯错误的概率,也就是Type I Error
A Type II Error is when you fail to reject the null when it is actually false.
![]()

9假设检验-零假设和对立假设.jpg
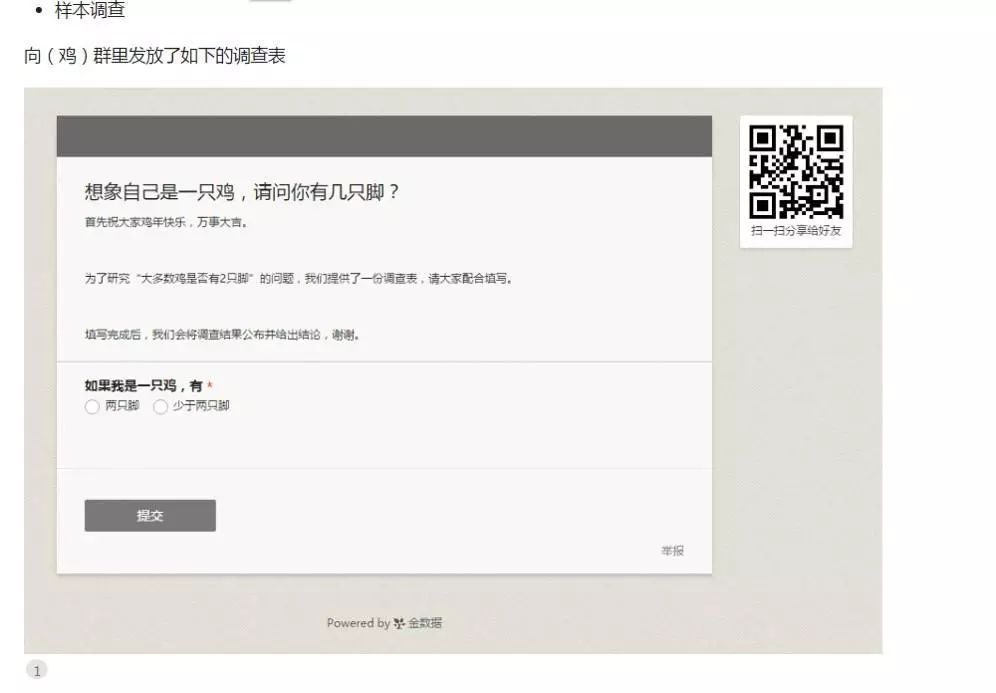
![]()
9.3假设检验-案例:鸡.jpg
![]()
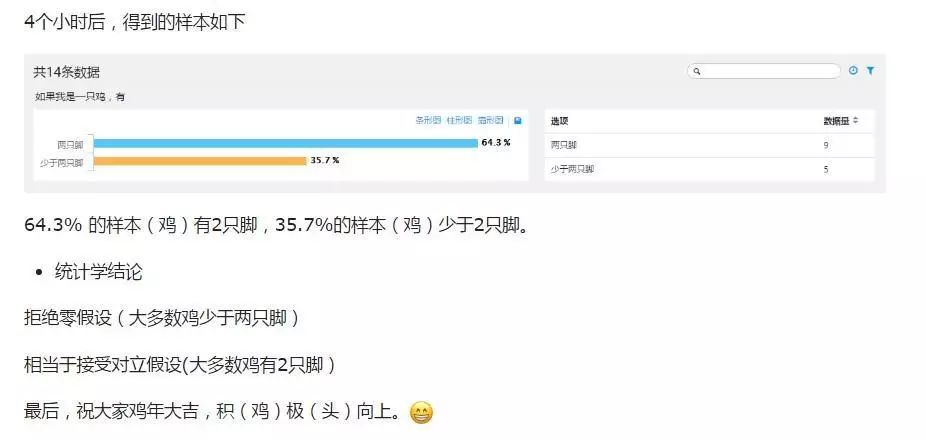
9.4假设检验-案例:鸡.jpg
作者:zhengweiyu 原文地址:https://discussions.youdaxue.com/t/topic/29031
2. 如何选择备选检验和零假设?
一个研究者想证明自己的研究结论是正确的,备择假设的方向就要与想要证明其正确性的方向一致;
同时将研究者想收集证据证明其不正确的假设作为原假设H0
推荐阅读:http://bbs.pinggu.org/thread-1071082-1-1.html
八、T检验(T-test)
1.
主要用于样本含量较小(例如n<30),总体标准差σ未知的正态分布。
流程如下:
![]()

10.t检验.jpg
是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著;
一般检验水准α取0.05即可;





