
以上解读为李文杰( 社区昵称:@月本诚 )在 AI研习社CVPR小组 原创首发,我已经努力保证解读的观点正确、精准,但本人毕竟才学疏浅,文中若有不足之处欢迎大家批评指正。所有方法的解释权归原始论文作者所有。
具有高标签利用率的图滤波半监督学习方法

本文解读了一篇被CVPR2019大会接收的半监督学习方向的论文,点击【阅读原文】到AI研习社CVPR小组查看原文。在之前AI研习社直播的CVPR论文分享会上,论文的作者之一吴晓明老师做了现场分享,大家可以将第一个回放视频跳转到1:59:23处听吴老师的现场讲解。本文基于论文原文和老师的PPT对文章内容进行了重新梳理和解读,详略适中,希望对大家有帮助。
《Label-Efficient Semi-Supervised Learning via Graph Filtering》一文研究了半监督学习问题,作者们提出了一种基于图滤波的半监督学习框架,并利用该框架对两种典型的图半监督分类方法LP和GCN进行了改进,新的方法不仅能同时利用图的连接信息和节点的特征信息,还能提高标签的利用效率,文中提出的改进方法在所有的实验数据集上都取得了最好的效果。作者用图滤波框架统一了看起来完全不同的LP和GCN,其“低通滤波”的观点精炼地解释了这两种方法在实际应用中奏效的原因,提高了研究者对于此类方法的认知水平。
1.预备知识
1.1 目标问题
图半监督分类问题即给定图G、图信号矩阵X以及节点标签矩阵Y(稀疏矩阵,只有部分节点有标签)要求输出标签矩阵Y’(给出每个节点的类别),以下图为例:
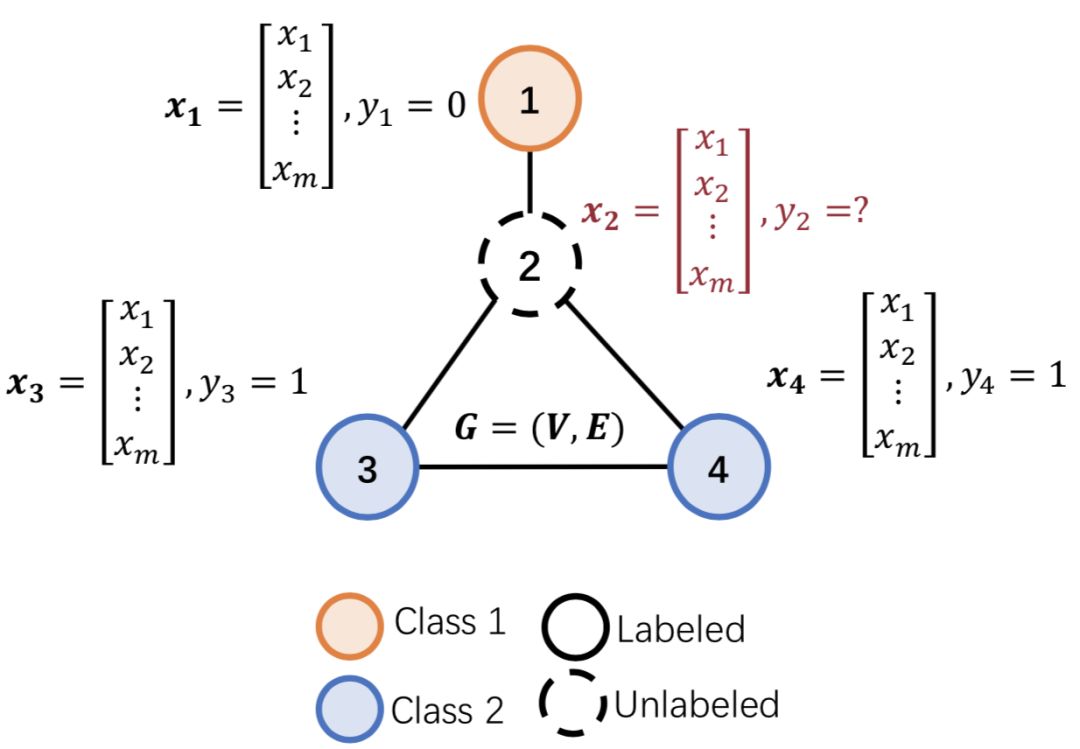
图中的节点1、3、4为有标记的节点、节点2为未标记的节点。每个节点对应一个特征向量x_ixi,半监督分类的目的就是利用所有节点的特征和已标记节点的标签来预测未标记节点(节点2)的类别。
图半监督分类根据节点之间的相似度来分配标签,节点间的相似度越高,其类别相同的概率就越高,于是便可以将其中一个节点的类别赋予另一节点。节点的相似性不仅由图的连接结构反映,也可能被节点的特征隐式的表达,所以只有综合利用节点的连接信息和特征信息才能得到更好的相似度表征,进而提高标签分配的正确率。
1.2 图的频谱分析
一个无向图可以用拉普拉斯矩阵L表示,对L进行特征分解可以得到一组标准正交的特征向量(可以组成标准正交基和正交矩阵),每个特征向量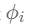 都有对应的特征值
都有对应的特征值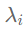 。在图信号处理领域中,这组标准正交基被称为图的傅里叶基(Fourier Basis)对应的特征值代表这个基信号的频率(Frequency)。相关定义见下式:
。在图信号处理领域中,这组标准正交基被称为图的傅里叶基(Fourier Basis)对应的特征值代表这个基信号的频率(Frequency)。相关定义见下式:
L = D-W
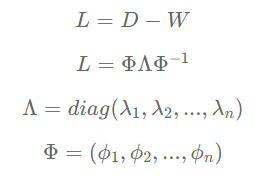
其中W为图的邻接矩阵,D为度矩阵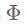 是L的特征向量按列排列而成的正交矩阵,
是L的特征向量按列排列而成的正交矩阵,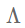 是L的特征向量组成的对角矩阵。值得注意的是,拉普拉斯矩阵有多种定义,以上第一个公式的定义只是最原始的一种。另外还有归一化的拉普拉斯和对称归一化的拉普拉斯定义如下:
是L的特征向量组成的对角矩阵。值得注意的是,拉普拉斯矩阵有多种定义,以上第一个公式的定义只是最原始的一种。另外还有归一化的拉普拉斯和对称归一化的拉普拉斯定义如下:
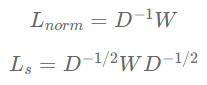
L_{norm} = D^{-1}W
它们的区别主要在“对称”和“归一化”上,差别并不是很大,为了避免读者混淆所以此处先将它们都列举出来。图信号的频率反映了它的变化程度,低频的信号较平滑,相邻节点的信号值相似度高,而高频信号的变化较为剧烈,相邻节点的信号值可能差异较大。频谱分析的目的是将复杂信号分解成某种相对简单的基本信号的线性组合,通过研究这些简单信号的性质及它们在原始信号中的占比就能推测出原始信号的性质,这是化繁为简、化大为小的解构主义哲学的体现。例如一维傅里叶变换将一维信号分解成复指数函数的线性组合(离散信号)或积分求和(连续信号)。而常用的二维图像DCT变换将图片分解成余弦基信号的线性组合。
类似的,在将此概念推广到图信号处理领域,基信号变成了拉普拉斯矩阵的特征向量 ,而任意的图信号都可以被表示成
,而任意的图信号都可以被表示成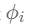 的线性组合(标准正交基的线性组合可以表示n维空间中的所有向量)。
的线性组合(标准正交基的线性组合可以表示n维空间中的所有向量)。
f = \Phi c = \sum_{i=1}^{n} {c_i \phi_i}
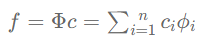
图信号(graph signal)就是在图上定义的信号,图中的每一个节点都对应着一个实数值,可以用向量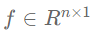 表示一个图信号,其中n代表图节点的个数。多变量的图信号或者说多维的图信号可以用矩阵
表示一个图信号,其中n代表图节点的个数。多变量的图信号或者说多维的图信号可以用矩阵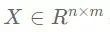 表示,此时每个图节点都对应一个长度为m的一维向量,该向量表示节点的特征。
表示,此时每个图节点都对应一个长度为m的一维向量,该向量表示节点的特征。
1.3 图卷积滤波
所谓“滤波”是指过滤掉信号频谱中的特定成分,比如说常见的低通滤波就是指尽量保留信号的低频成分并过滤掉其高频成分。可以将滤波看做一个信号映射函数,该函数接收一个原始信号并输出过滤后的信号。滤波一般通过在原始信号上乘以滤波器实现,论文中定义了如下的图卷积滤波器:
G = \Phi p(\Lambda)\Phi^{-1}
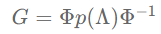
其中,函数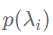 被称为频率响应函数。使用此卷积过滤器对图信号f进行卷积可得:
被称为频率响应函数。使用此卷积过滤器对图信号f进行卷积可得:
\bar f = Gf = \Phi p(\Lambda)\Phi^{-1} \cdot \Phi c = \sum_i^n p(\lambda_i)c_i\phi_i
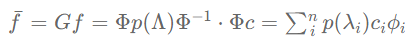
可以发现,滤波信号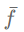 中每一个基信号
中每一个基信号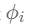 的比例
的比例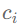 都被函数
都被函数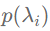 缩放了。频率响应函数控制着滤波器对不同频率的基信号的响应,我们可以设计不同性质的频率响应函数满足不同场景的滤波需求。
缩放了。频率响应函数控制着滤波器对不同频率的基信号的响应,我们可以设计不同性质的频率响应函数满足不同场景的滤波需求。
1.4 图滤波与半监督分类
图半监督分类的基本假设是“相邻节点的标签相似”,这意味着我们希望有标记节点周围的图信号是平滑的、低频的,我们期望学到低频的表示信号,所以应该使用具有低通性质的滤波器和频率响应函数。作者就是用这种“低通图滤波”的视角统一解释了LP和GCN并基于此做出了有效的改进。
2. 动机
经典的Label Propagation算法只能利用图的结构信息,无法利用节点的特征。而新兴的Graph Convolution Network需要大量的Label用来训练和验证,但半监督学习任务的标签数量本来就少,所以GCN在标签数据较少的情况下可能难以奏效,因为它的标签利用效率是低下的。为了解决LP不能利用节点特征的问题,作者对其做出了改进并提出GLP。为了解决GCN模型复杂度较高且标签利用率较低的问题,作者对其进行了改并进提出IGCN。两种方法都是在图滤波的框架下提出,在理论上可以被统一的解释,在实践中也都有很好的效果。
3. 方法介绍
3.1 图滤波与LP
1) 原始LP算法
标签传播算法(Lable Propagation)简称LP,是一种简单有效的图半监督学习方法,在科研和工业实践中均被广泛应用。LP的目的是得到一个能满足真实标签矩阵Y同时在图上又足够平滑的预测/嵌入矩阵Z。LP模型的优化目标如下:
Z = \arg min \lbrace ||Z-Y||_2^2 + \alpha Tr(Z^TLZ) \rbrace
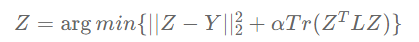
其中矩阵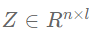 ,其中
,其中 表示类别的个数,矩阵的每一行表示一个节点的多类别预测概率(也可以视为节点嵌入向量)。优化目标的第一项约束预测矩阵与真实标签矩阵的误差尽可能小,第二项约束目标矩阵
表示类别的个数,矩阵的每一行表示一个节点的多类别预测概率(也可以视为节点嵌入向量)。优化目标的第一项约束预测矩阵与真实标签矩阵的误差尽可能小,第二项约束目标矩阵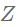 在图上的变换尽量平滑,被称为拉普拉斯正则项,正则的力度用参数
在图上的变换尽量平滑,被称为拉普拉斯正则项,正则的力度用参数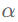 控制。这是一个无约束的二次优化问题,有解析解:
控制。这是一个无约束的二次优化问题,有解析解:
Z = (I+\alpha L)^{-1}Y
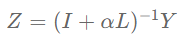
得到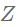 之后,可以直接选择每一行中取值最大的一类作为节点的类别,或者在此之前多做一步列归一化的操作。
之后,可以直接选择每一行中取值最大的一类作为节点的类别,或者在此之前多做一步列归一化的操作。
2) 图滤波视角下的LP
若从图滤波的视角看,可将LP算法分成3大部分:
1.图信号:标签矩阵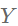
2.滤波器:低通滤波器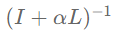
3.分类器: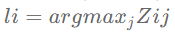
其中,滤波器:
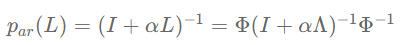
p_{ar}(L) = (I+\alpha L)^{-1}= \Phi(I+\alpha \Lambda)^{-1}\Phi^{-1}
满足上文中卷积滤波器的定义,被称为自回归(Auto-Regressive)滤波器,其激活响应函数为:
p_{ar}(\lambda_i) = \frac{1}{1+\alpha \lambda_i}
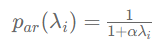
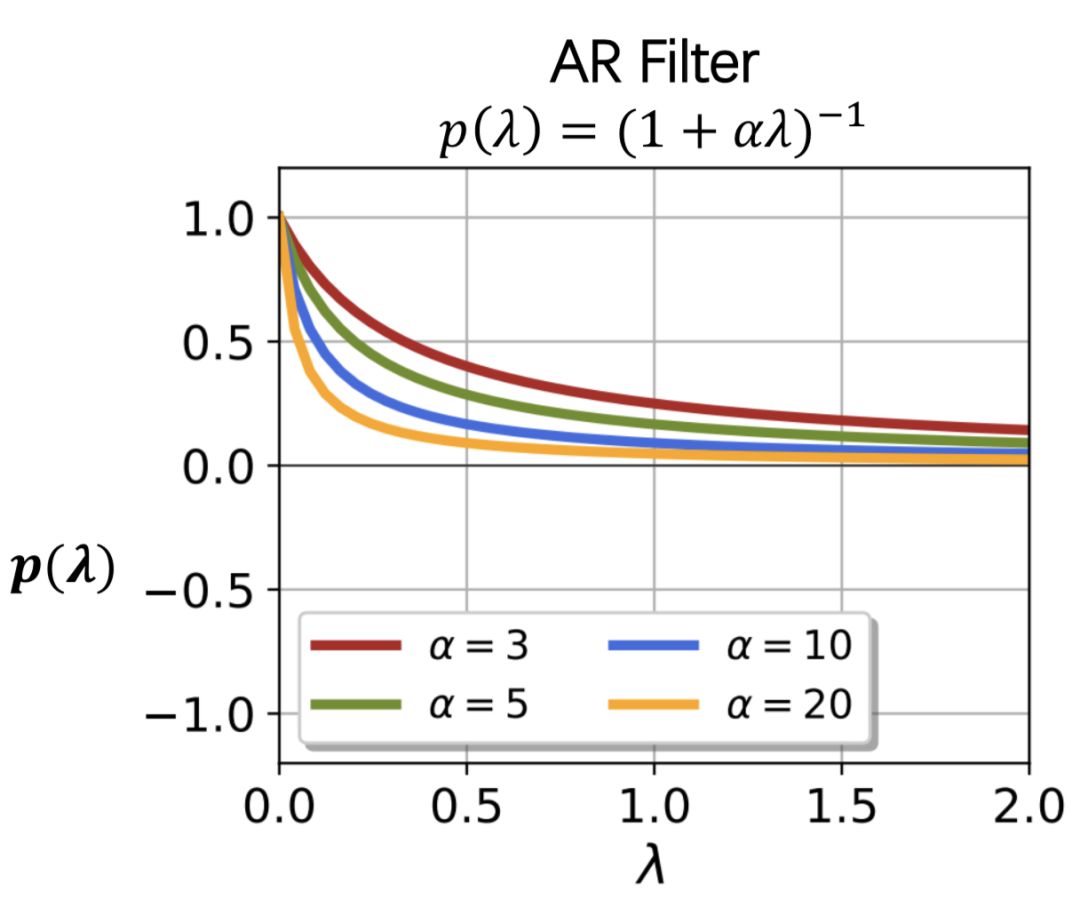
从下图来看,自回归滤波器显然是低通的、抑制高频的,其平滑力度随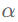 的增大而增大。
的增大而增大。
3) 推广的标签传播算法GLP
作者将图滤波视角下LP的三大组件进行了推广泛化,提出了广义标签传播算法(Generalized Label Propagation)GLP。具体推广如下:
1.图信号:使用所有节点的特征向量组成的特征矩阵X作为输入信号
2.滤波器:可以是任意满足定义的低通图卷积滤波器
3.分类器:可以是在带标签节点的嵌入表征上训练得到的任意分类器
这个推广非常自然,也很容易理解,最关键的步骤是对节点特征矩阵进行低通图滤波。这一步可以视为特征提取过程,作者利用低通滤波器提取出了更平滑的数据表征,并且同时考虑了图的连接信息和节点特征信息,弥补了原始LP无法利用节点特征的缺陷。而滤波器与分类器的推广泛化则大大提高了算法的灵活性,使GLP很容易就能整合到不同的问题领域。
3.2 图滤波与GCN
1) 原始GCN
GCN是一种在频谱上定义的图卷积网络,它简单有效,在半监督分类问题上有优异的表现。GCN首先对邻接矩阵加入自连接并进行对称归一化得到重归一化矩阵 :
:
\tilde{W} =W+I
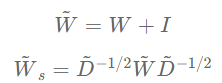
第一个式子相当于引入了各节点到自身的连接,第二个式子中 是矩阵
是矩阵 的对称归一化拉普拉斯矩阵。基于
的对称归一化拉普拉斯矩阵。基于 ,原文作者定义GCN的层级传播过程为:
,原文作者定义GCN的层级传播过程为:
H^{(t+1)} = \sigma \left ( \tilde{W}_s H^{(t)}\Theta^{(t)} \right)
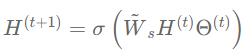
其中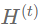 表示第t层的输入,
表示第t层的输入,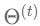 是第t层的待学习参数,σ可以是神经网络中的各种激活函数。
是第t层的待学习参数,σ可以是神经网络中的各种激活函数。
一层图卷积先对输入信号左乘以重归一化矩阵 ,然后再使用参数矩阵Θ进行投射变换,最后使用激活函数进行非线性变换。堆叠多个图卷积层后最后使用softmax激活函数进行分类,比如双层图卷积:
,然后再使用参数矩阵Θ进行投射变换,最后使用激活函数进行非线性变换。堆叠多个图卷积层后最后使用softmax激活函数进行分类,比如双层图卷积:
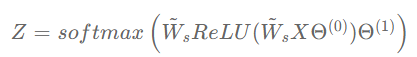
Z = softmax\left( \tilde W_s ReLU(\tilde W_s X \Theta^{(0)})\Theta^{(1)}\right)
可以使用反向传播算法对此GCN进行训练得到最终模型。
2) 图滤波视角下的GCN
从双层GCN的式子中可以看到,GCN其实就是不断地重复着1) 左乘 2)投射变换 3)激活变换 三个步骤。其中投射变换和激活变换是普通神经网络中的通用操作,而“左乘”重归一化矩阵可以看做对输入信号进行图滤波,因为重归一化矩阵满足:
\tilde W_s = I-\tilde L = \Theta(I-\tilde \Lambda)\Theta^{-1}
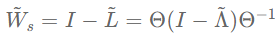
其中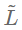 为矩阵
为矩阵 的对称归一化拉普拉斯。滤波器
的对称归一化拉普拉斯。滤波器 对应的频率响应函数为:
对应的频率响应函数为:
p(\tilde\lambda_i) = 1-\tilde\lambda_i
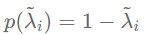
如果我们将双层GCN中3个操作的顺序稍微替换一下,将两个图滤波步骤全部放在第一层,比如:
Z = softmax\left(ReLU(\tilde W_s^2 X \Theta^{(0)})\Theta^{(1)}\right)
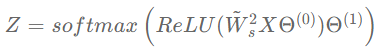
此时的GCN就变成了GLP的一种特殊情形,其滤波器为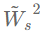 ,输入信号为X,分类器为双层感知机,
,输入信号为X,分类器为双层感知机,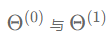 便是感知机中每一层的权重矩阵。k层GCN可视为滤波器为
便是感知机中每一层的权重矩阵。k层GCN可视为滤波器为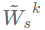 ,输入信号为X,分类器为k层感知机的GLP,滤波器的频率响应函数为:
,输入信号为X,分类器为k层感知机的GLP,滤波器的频率响应函数为:
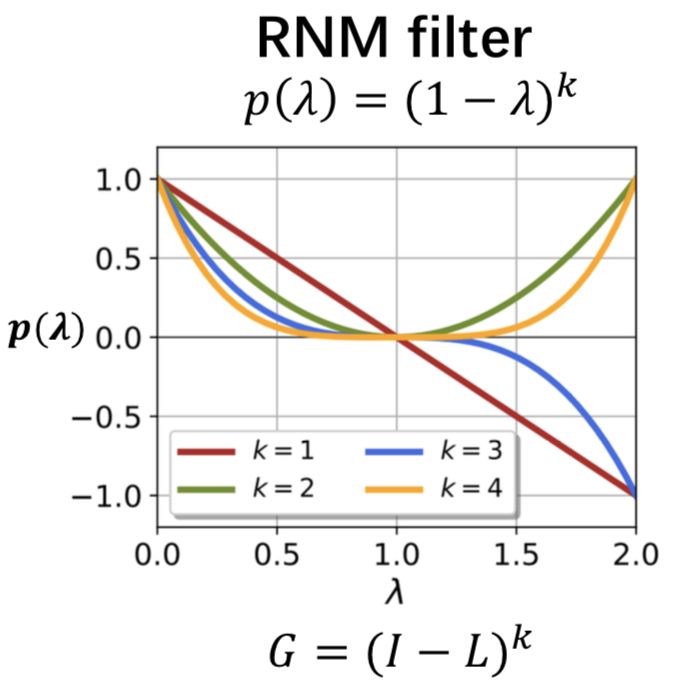
p(\tilde\lambda_i) = (1-\tilde\lambda_i)^k
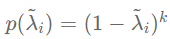
从下图可以看到,该滤波器在[0,1]区间内是低通滤波器,且其低通程度随k的增大而增大。所以多层GCN的滤波器比单层GCN的滤波器更加低通,平滑力度更大。
在图滤波的视角下,我们可以用频率响应函数的性质来解释GCN 1) 使用对称化归一化拉普拉斯定义 2) 使用重归一化技巧(添加自连接) 的原因。采用对称归一化拉普拉斯矩阵可以将特征值的取值范围限制在[0, 2]之间,而重归一化技巧可以将特征值的取值范围进一步缩小,这促使滤波器越来越接近于完全低通。 作者在Cora数据集上对重归一化前后GCN的频率响应函数进行了可视化,如下图所示:
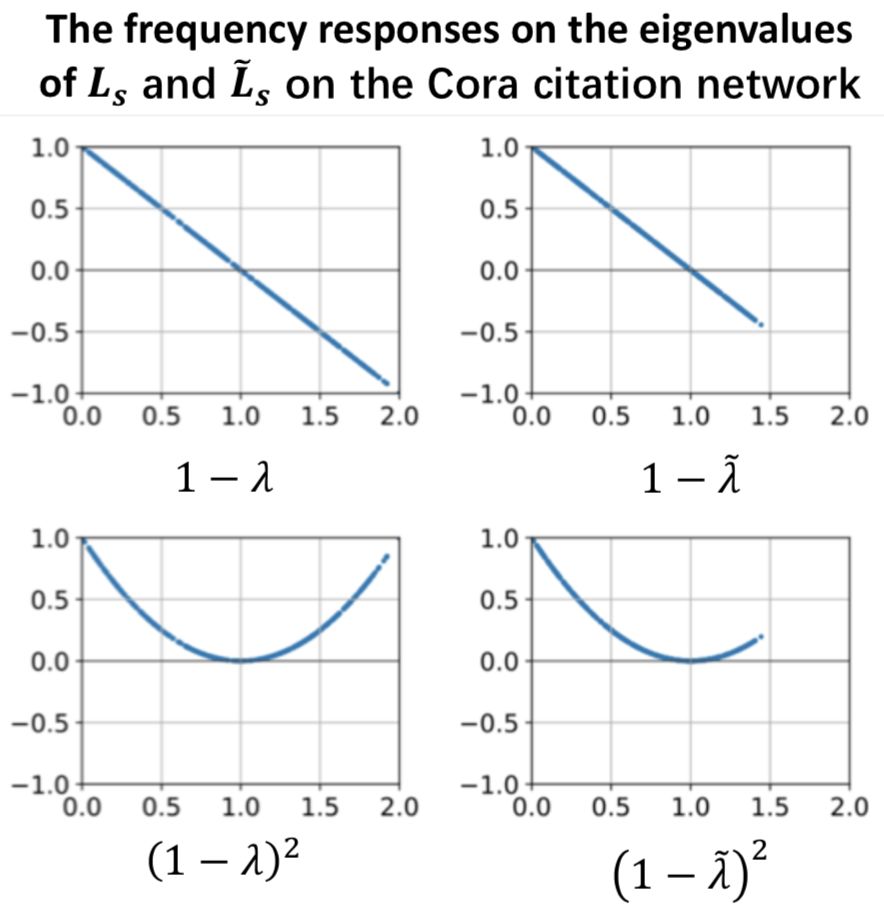
可以看到,无论是单层还是双层,重归一化后的拉普拉斯矩阵的特征值都被限制到了1.5以内,验证了作者们对于重归一化技巧在应用中奏效的解释。事实上,可以证明重归一化技巧能使拉普拉斯矩阵的特征值范围压缩到区间:
[0, \frac{d_m}{d_m+1}\lambda_m]
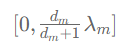
其中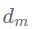 表示图中节点度(Degree)的最大值,
表示图中节点度(Degree)的最大值,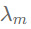 为对称归一化拉普拉斯矩阵的最大特征值。
为对称归一化拉普拉斯矩阵的最大特征值。
3) 图滤波增强版GCN
虽然堆叠多个GCN层可以增加滤波的平滑力度,但也会引入更多待学习参数,这使得网络需要更多的数据训练以避免过拟合。为了解决这个问题作者提出了IGCN(Improved Graph Convolutional Network)。IGCN将GCN中的重归一化矩阵全部替换成了重归一化滤波器,即:
Z = softmax\left( \tilde W_s^k ReLU(\tilde W_s^k X \Theta^{(0)})\Theta^{(1)}\right)
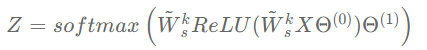
作者称滤波器:
p_{rnm}(\tilde L_s) = \tilde W_s^k
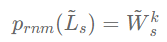
为重归一化(Renormalization)滤波器,其频率响应函数为:
p_{rnm}(\lambda) = (1-\tilde\lambda)^k
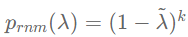
显然,IGCN可以通过调节k来直接控制滤波的平滑力度且不会引入额外的待学习参数,这可以使模型维持在浅层水平,无需过多数据即可达到理想的训练效果,提高了模型的标签利用效率。
4. 实现与验证
4.1 平滑力度与计算性能
无论是GLP还是IGCN,都可以通过控制参数或者参数k来控制滤波的平滑力度,那么应该如何根据应用场景调整平滑力度呢?作者指出数据集的标签率是调整平滑力度的一个关键参考,当标签率较小时平滑力度应该较大,以使较远的无标签节点也能与有标签节点获得相似的特征表示;当标签率较大时,平滑的力度应该较小,标签的传播范围不宜太远,以保持特征的多样性。作者使用不同平滑力度的RNM滤波器在Cora数据集上做了实验并做了t-SNE可视化,其结果如下:
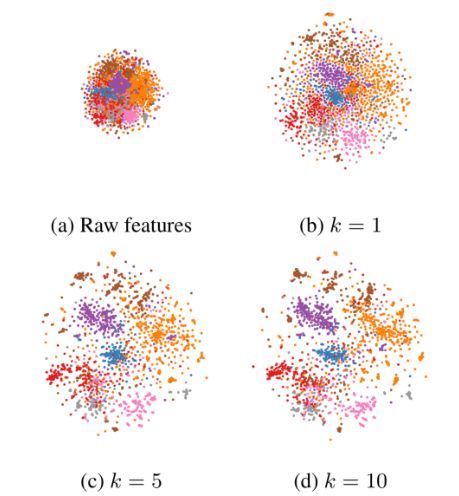
可以发现,随着平滑的力度增大,滤波结果的类簇变得越来越紧凑,簇间距越来越大,分类边界也变得更加清晰,此时只需要少量的标签便可以进行分类,这就直观地解释了平滑力度设置与数据标签率之间的关系。
除了平滑力度外,文中还讨论了两种滤波器的计算性能。由于AR滤波器涉及到了运算代价很高的矩阵求逆运算,作者使用k阶展开多项式来进行近似以降低计算复杂度。对于k阶RNM滤波器,可以利用拉普拉斯矩阵在实际应用中往往是稀疏的特性来进行计算加速。作者在文中分析了两种滤波器在理论上的计算复杂度,旨在说明其实用性。
4.2 半监督分类任务实验对比
作者在4个引文网络数据集和1个知识图谱数据集上进行了半监督分类任务的实验,并与许多出色的模型进行对比,包括Youshua Bengio团队的GAT。几个数据集的节点规模、类别数量以及特征数量均不相同,这样的实验安排能够衡量模型在各种场景下的表现,比较全面。各数据集的统计指标如下表:
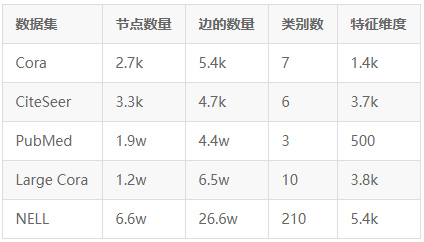
为了方便了解数据的量级,我使用k(千)和w(万)对数据进行了简化表示。除了选用不同规模的数据集,作者还为数据集设置了不同的标签率以观察平滑力度与标签率之间的关系,其设定如下表:
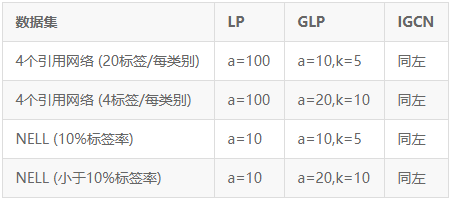
各模型在各数据集上的分类正确率如下:
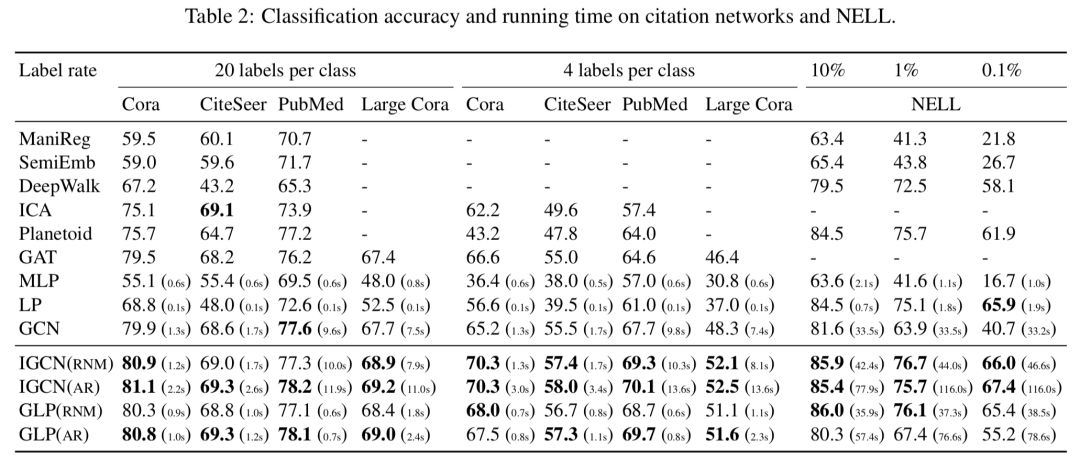
实验结果显示,经图滤波改造的方法在所有场景下的表现均优于其他对比模型。但从运行时间上来看,GLP与IGCN的耗时显然要更多一些,在规模较大的NELL数据集上最为明显,不过总的来说是在可接受范围内的。
4.3 Zero-Shot半监督回归任务实验对比
除了分类,GLP和IGCN还可以用于半监督回归。2018年CVPR的一篇论文使用GCN做了0样本图片识别(Zero-Shot image recognition)任务,即只使用类别的文字描述和类别之间的关系为没有任何训练样本的类别(Unseen Class)学习一个视觉分类器。该文在给定一个已知类别的分类器的前提下,使用每个类别的文字描述嵌入特征和类别关系作为输入,并以已知分类器最后一层的权重为回归目标训练了一个6层的GCN,然后将GCN的输出作为未知类别的分类器最后一层的权重,并使用新的权重组成分类器对所有类别进行预测。该文将Zero-Shot学习巧妙的转化成了图半监督回归问题,这使许多半监督回归方法都能应用于0样本学习任务,该文方法(GCNZ)的整体流程如下图所示:
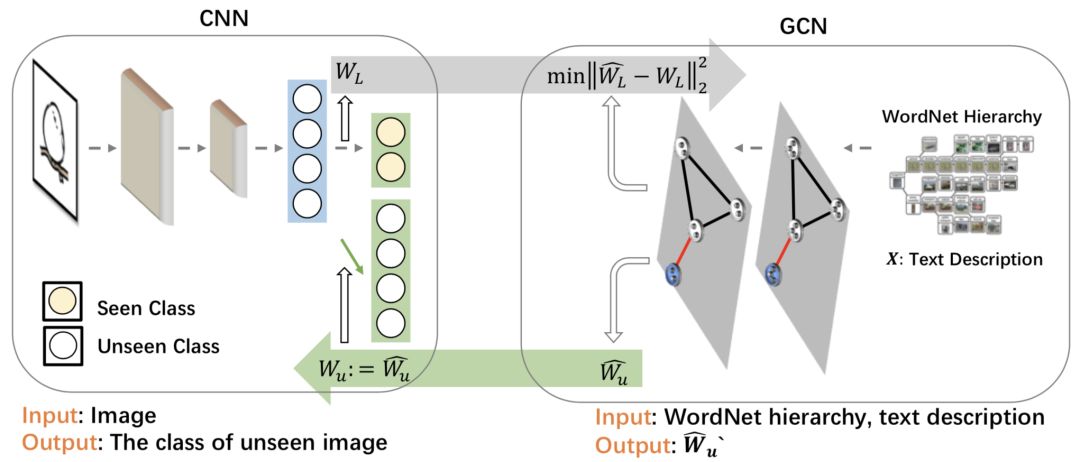
作者使用GLP和IGCN替换了此文中的GCN,并在AWA2数据集上使用一个预训练的ResNet-50网络进行了0样本学习任务的实验,各模型的性能对比结果如下表:

可以看到,IGCN的效果最好。由于GCNZ在发表时已经是State-of-the-art级别了,其核心组件是GCN,而GLP和IGCN又比GCN效果好,所以对于它们在0样本图片识别任务上的提升是有预期的了,这个实验说明了图滤波方法应用的广泛性。作者已将源代码公布至其github仓库。
5. 总结
总的来说,图滤波的想法是又简洁又实用的,虽然看起来简单但是理解却很深刻,有很强的理论指导意义和实践意义。合上这篇论文,只需记住“低通滤波”四字精髓。由于半监督分类问题是追求平滑和低通的,所以文章就以低通滤波为例为我们展示了图滤波的简洁和强大,但图滤波的框架和思想在“非低通”的问题上也是一贯适用的,例如我们可以设计中通的、高通的滤波器来解决相关的问题。我认为这篇论文的重要贡献是给图半监督学习打开了思路,提供了一条宽阔的路线,相信基于图滤波还可以做不少文章。我从这篇文章再次感受到了对原理的思考与探索的重要性,所有的改进和提升都离不开对原理和运作机制更深的了解。希望日后能在CVPR上看到更多有洞见的,有强解释性的文章。

每天进步一点点
扫码参与每日一题
扫码查看
【现代自然语言处理最佳/最新进展(文献阅读清单)】

今天距离CVPR 2019开幕就剩 23 天啦!![]()
明天AI研习社将公布CVPR 2019的
顶会赞助计划最终名单,敬请关注!
左右滑动查看更多内容
 点击 阅读原文 ,查看更多内容
点击 阅读原文 ,查看更多内容














