有些讲傅里叶级数的文章涉及的内容较深，对于一些数学知识不够的学生来说有点儿难以看懂。本文从较基本概念出发，试图将傅里叶级数的基本概念讲清。由于本人才疏学浅，错误地方在所难免，望大家不吝赐教。
阅读本文有一个要求：希望大家能够跟着计算，这样才能真正理解。
首先，我们从最基本的矢量出发。
我们都知道:
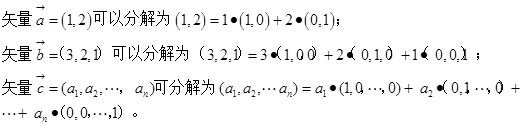
相信大家都知道
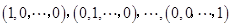为空间中的
n
个单位正交基。我们规定
R
n
中的一组基
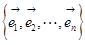，若满足
=
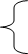
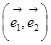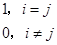i
，
j=1,2
，···，
n
那么称其为单位正交基。通过这组基可以表示由这组基张成的
n
维空间中的任何向量。那么，对于一个由无数函数构成的无穷维函数空间，是否也存在这样一组基呢，使得任意函数均可由这组基表示？答案是肯定的。不过在讲这组基之前，我们先介绍一下函数内积的概念。
一般来说
,
在闭区间
[a,b]
上
,
两个连续函数
f(x),g(x)
的内积定义为二者乘积在
[a,b]
上的黎曼积分，即
,
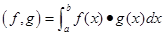同样我们类比定义函数空间中的一组单位正交基
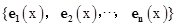，满足
,
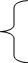
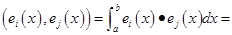
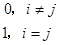i, j=1,2,
···，
n
现在，我们来讲函数空间中的那组正交基。
傅里叶在对热传导问题的研究中为了求解偏微分方程而建立了傅里叶级数，傅里叶级数理论表明任何一个函数都可以用三角函数的和来表示，而这些三角函数正是傅里叶找到的那组正交基：
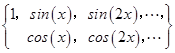
我们也称此为三角函数系。
下面我们来验证一下，三角函数系是否满足正交基的定义。对于三角函数我很很自然会取闭区间
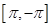
①
（
1
，
sin
（
kx
））
=
；
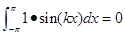k=1,2
，···
②
（
sin
（
kx
），
sin
（
hx
））
=
；
；
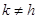k
，
h=1,2,3
···
③
（
cos
（
kx
），
cos
（
hx
））
=
；
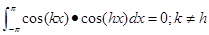k
，
h=1,2,3
···
注：利用积化和差公式很容易求得上述结果
④
（
1,1
）
=
；
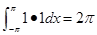⑤
（
sin
（
kx
），
sin
（
kx
））
=
；
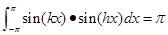⑥
（
cos
（
kx
），
cos
（
kx
））
=
；
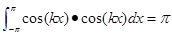从①～⑥可以看出三角函数系的确是一组正交基，但由于函数与自身的内积不为
1
，故这组基不是单位正交基。
类比矢量的长度，我们定义函数的长度（以区间
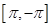，为例说明）
∣
∣
=
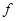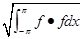
通过这个，我们便可以对基进行单位化：
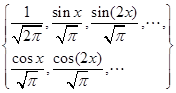
当然，为了方便我们也可以不用单位正交基，而只用正交基，于是任意函数
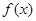可以表示为
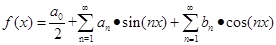
三角函数前的系数为该函数在这一个基上的分量。类比向量分量的运算：
，
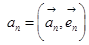其中
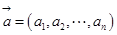。我们定义函数在某一基上的分量为
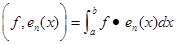
其中
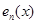表示函数空间中的某一基。
于是，我们可以求得
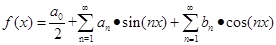中的
，
，
，
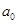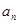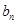计算方式如下：
⑴
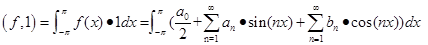
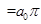
故
；
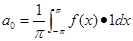⑵
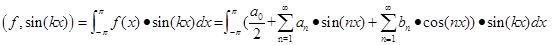
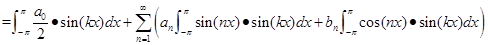
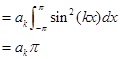
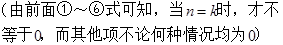
同理
⑶
；
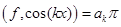于是，
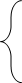
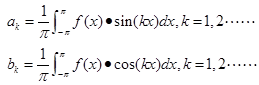
综合⑴～⑶可得
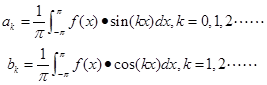
这个式子即为系数的表达式，如果是用单位正交基，那么直接内积后便可得系数。
这与泰勒级数一样，虽然都求出了系数，但却不一定能够收敛到
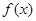，这是有条件的。这个条便是狄利克雷收敛定理。有兴趣的可以自行查阅数学分析教材或高等数学教材。
这样我们就基本弄清了傅里叶级数的模样，更深内容留待大家自行学习。
参考文献：
⑴
《高等数学》，天津大学数学系，高等教育出版社；
⑵
课堂笔记
