
▲
点击上图,成为会员
超过13万人在听
每天半元钱,听吴晓波说世界万千
民主好还是专制好?
恐怕所有人都会投向民主。
但民主究竟是什么?
支持民主的人们会发现,彼此的理解并不相同。
例如,在美国当地时间2月21日刚刚去世的经济学巨匠肯尼斯·阿罗眼中,民主并不一定反映着“公共意志”,而且不同的制度设计,会直接影响民主的结果。

为纪念这位伟大的经济学家,乃至一个伟大时代的逝去,吴老师今天在音频中讲述了阿罗的生平和时代【点击收听】,小巴就来讲讲阿罗提到的“民主困境”。
文/巴九灵(微信公众号:吴晓波频道)
川普和希拉里的这场美国大选,很多吃瓜群众注意到一件事:希拉里获得的选民票却多于川普(47.66%:47.5%),却输了整场大选。
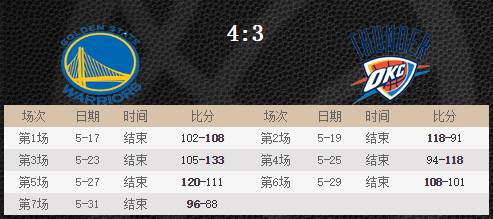
简而言之,原因就像勇士队和雷霆队的这七局比赛,虽然比分加和是743:750,雷霆队更多;但决定胜利的方式是获胜场次,所以勇士队7局4胜。
同理,希拉里获得了更多的选民票,但决定胜利的方式是,谁赢得更多州的选举人票,所以川普赢了。

你可能开始发觉民主投票有点闹心了,但这还只是两位候选人的情况。
假设有一天,我们要选出“国民水果”,候选者有苹果、西瓜和香蕉。
投票人有三位,巴八灵、巴九灵、巴零灵。
他们投票时,三种水果的排序是这样的:
巴八灵:苹果>西瓜>香蕉
巴九灵:西瓜>香蕉>苹果
巴零灵:香蕉>苹果>西瓜
尴尬了。
多数人认为西瓜优于香蕉,多数人认为香蕉优于苹果,多数人认为苹果优于西瓜。

这就是著名的“孔多塞悖论”:公共选择的偏好,成了一个循环。
2000年,维基百科的一次改版方案投票就采取了孔多塞制,结果五个方案里:方案1打败了方案4,方案4打败了方案3,方案3又打败了方案1……惨不忍睹。
这时,有人提出了另一种投票方式:我们给排名计分!例如巴九灵认为“西瓜>香蕉>苹果”,就给西瓜3分,香蕉2分,苹果1分。
最后汇总,西瓜共得X分,香蕉共得Y分,苹果共得Z分,就可以排序了。
在上文三人投票的例子中,最后西瓜、香蕉和苹果会同得6分,但是当投票人数变多,差距就拉开了。时至今日,一些国家的大选,一些比赛的最佳球员评选,仍会采用这种“波达计数法”。

但是这个方案仍然有许多问题:
① 可以通过参选人数影响排序;
三种水果一同参选时,每种各得6分,并列第一。
但是如果香蕉放弃参选了:
巴八灵:苹果(2分)>西瓜(1分)
巴九灵:西瓜(2分)>苹果(1分)
巴零灵:苹果(2分)>西瓜(1分)
苹果就以5分胜过西瓜的4分,改变了平局局面。但其实民众内心的偏好没变,只是候选人的数量变化了而已。
② 为了帮助心爱的水果获胜,选民可能故意把最有力的竞争者排在最后;
巴六灵:榴莲>西瓜>香蕉>苹果
巴七灵:榴莲>苹果>西瓜>香蕉
巴八灵:苹果>西瓜>香蕉>榴莲
巴九灵:西瓜>香蕉>苹果>榴莲
巴零灵:香蕉>苹果>西瓜>榴莲
例如这种情况下,如果按照一人一票制,榴莲原本是最受欢迎的选择。
但如果按照积分制,榴莲的排名却会垫底。
或许巴八灵、巴九灵、巴零灵的内心是把榴莲排在第二的,但是为了增加自己最爱水果的获胜概率,必须把它排在最后。
1991年,太平洋岛国基里巴斯举行大选,政府党派支持者就是通过这种方式,把威胁最大的对手排在最后,使得党派候选人成功当选。

现在,你是不是觉得设计一种完美的投票制度挺难的?
1951年,肯尼斯·阿罗基于种种坑爹的投票案例,通过数理化的方法证明出了一般性的结论——阿罗不可能性定理。
怎么证明的就不给你们讲了,毕竟太复杂你(wo)也看不懂。简而言之,就是当候选人至少有3位而投票人数有限时,无法同时实现以下五个理想的条件:
①所有人自由表态;
②如果所有人认为苹果优于西瓜,那最终结果应该也是;
③没独裁者,某人偏好不能直接决定最终结果;
④我更爱苹果/西瓜,不受香蕉参不参选影响;
⑤如果所有人都不改变自己更爱苹果还是西瓜的偏好,那即使对香蕉的偏好改变了,也不会影响苹果和西瓜之间的相对排名。
是不是觉得这五点都挺理所当然的?然而数学推导证明,它们不可能共同实现,比如达成了①②④⑤,就一定会出现独裁者。
这就是“阿罗不可能性定理”,虽然它描述的是很抽象的情况,却仍然对我们反思民主制度有所帮助:众多个体的偏好没那么容易汇聚成某种共识。

1972年,51岁的阿罗凭借一般均衡理论获得诺贝尔经济学奖,也成为至今最年轻的获奖者。但在他的眼中,社会选择理论(包含阿罗不可能性定理)才是自己最重要的贡献。
当然,除了理论贡献,他还教出了四位诺奖得主。
2017年2月21日,95岁的肯尼斯·阿罗去世。算上2006年去世的弗里德曼,2009年去世的萨缪尔森,2013年去世的科斯、布坎南、阿尔钦,2014年去世的贝克尔……那个经济学群星闪耀、突飞猛进的年代正在离我们远去。

重整河山待后生,尤其是,期待中国经济学界的“后生”。

跟吴晓波去汉诺威
了解前沿机器人和智慧工厂
对接百名中德企业家/对话中德智造
参观西门子、大众、奔驰、ABB等标杆名企
点击下图,了解更多
▼















