
圆锥曲线历来是高考的重中之重,但是最近不少考题的求解中过分依赖于繁杂的计算,使得学生对此黯然伤神。本文希望用若干个有趣的例子,充分发挥几何证明的威力,简化计算。让学生在掌握重要结论的同时,充分发挥思维上的想象空间,并综合利用各方面的知识,从解题中获得学习乐趣。
1. 椭圆——天使之眼
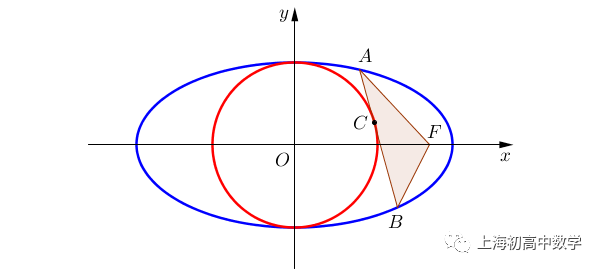
椭圆里用得最多的应该是中点弦的相关性质,可以看作是圆的垂径定理在椭圆中的一般化。本文介绍的这个例子也和圆有关,结论相当简洁优美,当然,这个例子来源于徐汇区某校的一道考题。我把它一般化了。

(这个图不是很标准,当然这并不重要)
一般化后的结论:已知标准椭圆
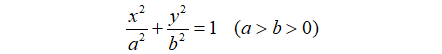
以椭圆短轴为直径作圆O,椭圆右焦点为F,过点C(y轴右侧)作圆的切线与椭圆交于A、B两点,则有结论AF+AC=BF+BC=a,或者,△ABF的周长为2a
证明过程如下所示,设点A(m、n),m>0
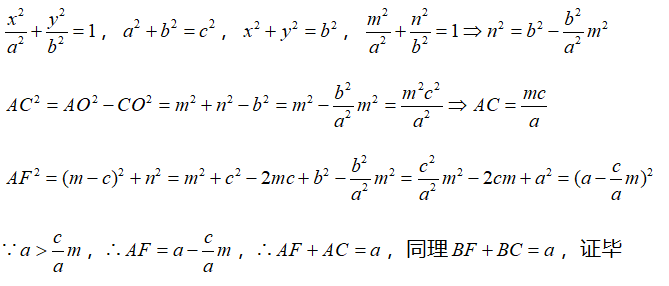
整个证明过程都是字母,本以为会相当繁琐复杂,却不想再一次被“
设而不求
”的简洁而优美的解析几何所征服。如果用平面几何处理,应该会很难算。这道题完美呈现了解析几何的力量和美感。有欲擒故纵的深远,有出人意料又仿佛情理之中的天衣无缝,甚至有不劳而获的确幸感,美如天使
当然,本例的切点和焦点在同一侧,如果在异侧,结合上述证明过程,不难得到AF-AC=BF-BC=a
2. 双曲线——等轴等距
对于等轴双曲线 x²-y²=m²,有这样的一个性质 (如图所示):如果一条直线和双曲线的一支相交于两点A和B,和这一支两侧的渐近线交于点C和D,那么AC=BD.
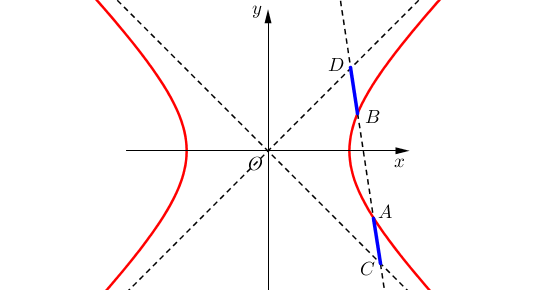
为了简化计算过程,增加问题的趣味性,我们分两步完成证明,同时揭示一下双曲线重要的几何特点。首先回忆一下反比例函数 y=k/x 的性质,如图所示
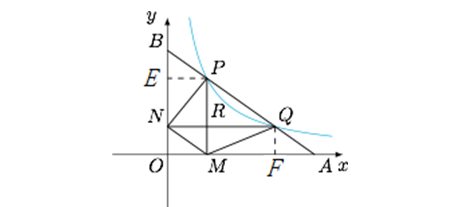
由反比例函数的性质可以得到矩形
EPMO
和矩形
QNOF
面积相等,减掉公共部分矩形NRMO,则矩形EPRN和矩形QRMF面积相等,所以它们的一半:三角形
PRN
和三角形
QRM
面积相等。加上公共部分三角形PQR,则三角形
PNQ
和三角形
PQM
面积相等。
又因为三角形PNQ和三角形PQM具有公共底边PQ所以它们的高应该相等,可以得到NM平行于PQ,所以四边形BPMN和四边形QNMA均为平行四边形。由对边相等可以得到:BP=MN以及QA=MN,至此我们证明了:
BP=QA
。
接下来我们通过一个简单的例子来证明许多老师上课时提到的一个结论:
等轴双曲线是反比例函数旋转45°得到的。
先看一下坐标旋转的概念。在下图中,有两套坐标体系:xOy和XOY,它们之间旋转了 θ 角,对于某一个特定的点,其坐标在两个体系中分别表示为 (x,y) 和(X,Y),
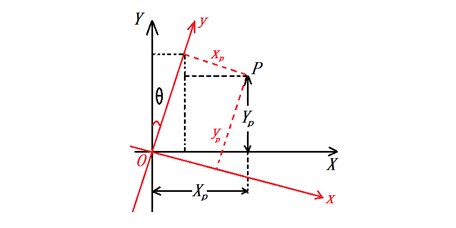
它们的转换关系可以很容易的从图中得到
X=ysinθ + xcosθ
Y=ycosθ-xsinθ
当θ=-45°时,
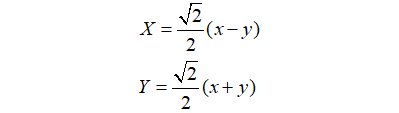
当P点在XOY坐标系中满足Y=k/X时,在xOy坐标系表示为:x²-y²=2k,即反比例函数旋转45°就得到等轴双曲线,原来的X轴,Y轴变成了对应的渐近线。
至此,我们利用简单的几何方法证明了等轴双曲线的割线性质。
3. 抛物线——万剑归一
抛物线有一个很好的光学性质:
平行于对称轴的光线入射后都会聚焦到抛物线的焦点
。翻译成数学语言就是:过抛物线上的任意一点P作切线,切线倾斜角等于切线和FP的夹角(其中F为抛物线焦点)。(即图中∠APC=∠BPF)
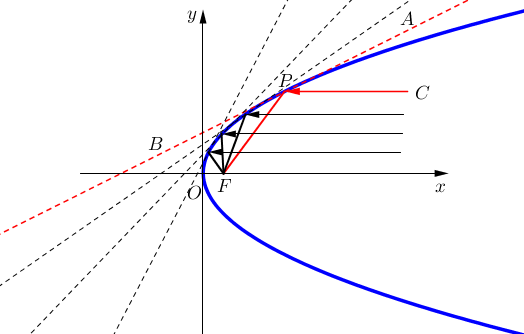
证明如下:先求过抛物线y²=2px上一点P的切线方程,不同于传统上设直线方程,联立方程组消元,利用二次方程判别式为零的方法,这里利用切线的严格定义和极限计算技巧,也希望同学对切线的理解更上一层楼。
很多学生对切线的理解,仅限于初中圆的切线。但是必须强调一点,和曲线只有一个交点的直线未必是切线(反例有很多,例如上图中,平行于x轴的任意曲线都和抛物线有且仅有一个交点,但显然不是切线)。
切线是割线的一种极限,当直线和曲线的两个交点无限靠近时,割线就变成了切线。
我们先计算过抛物线上两点
(如下)的割线斜率
k
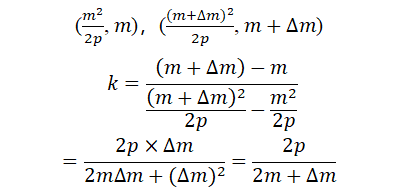
切线斜率为
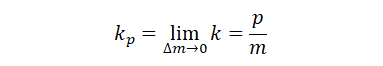
因此,过
P
点的切线方程用点斜式表示为:
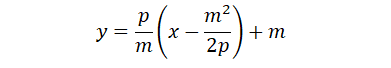
而过点
F
点和
P
点的直线方程为:
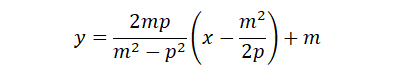
该直线和切线的夹角的正切为:
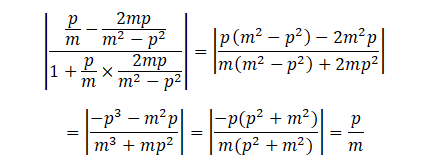
至此,可得:抛物线切线倾斜角和切线与
FP
的夹角是相等的,即证明了平行于对称轴的光线入射后都会聚焦到抛物线的焦点。
4. 抛物线——弯弓射雕
说起两个角相等,不由得想起这个例子,已知A(p,0),直线x=-p上有一动点B,O是坐标原点,∠AOB的角平分线与AB的交点的轨迹方程为y²=px
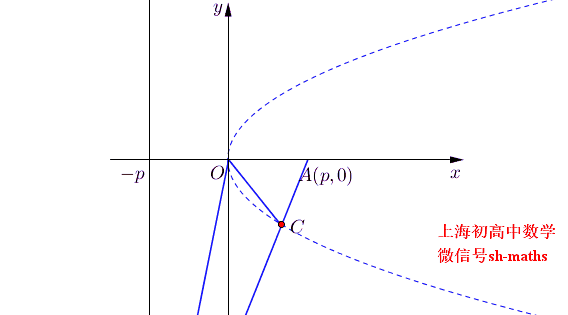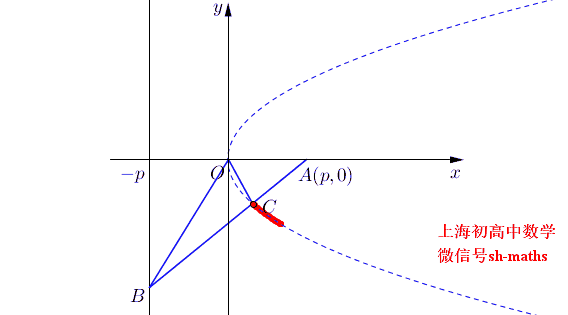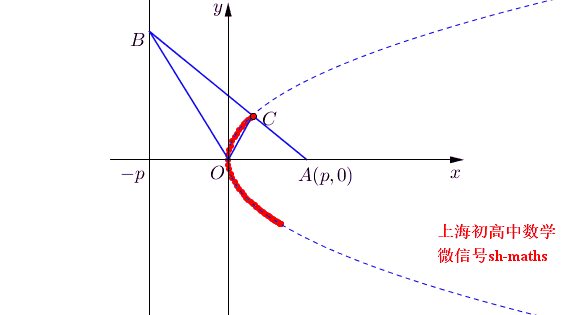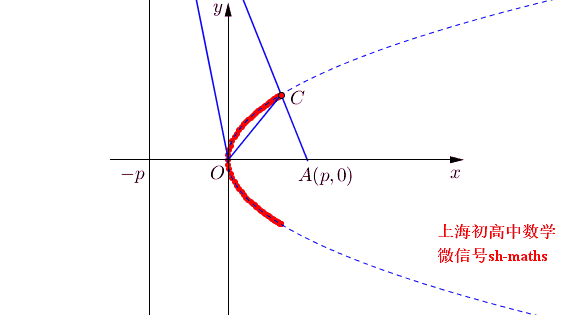
证明如下,设直线OC为y=kx,则直线OB为
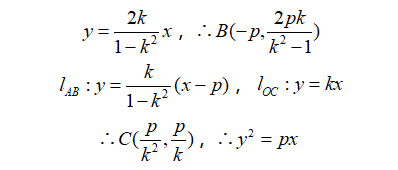
当然,这里的A点并不是该抛物线的焦点,而关于抛物线的焦点弦,则有更多的性质,在
《降龙十八章》
中第十二章我有罗列,这些常见性质,我就不一一证明了
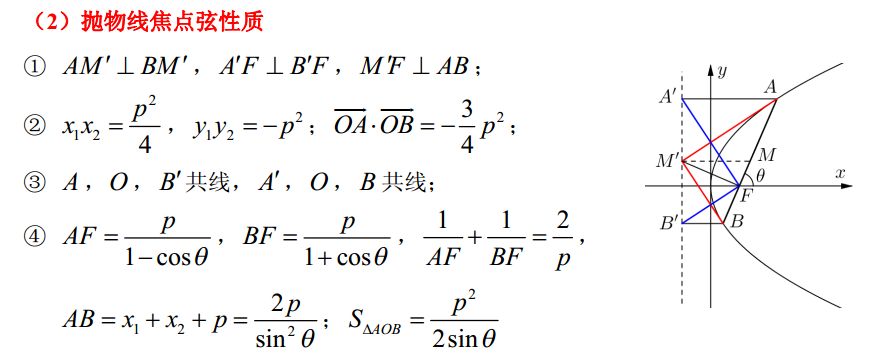
最后,希望本文能起到一个抛砖引玉的效果,让大家来分享更多有趣的例子,让更多人发现解析几何的魅力,体会“设而不求”的简洁优美,感受这些看似巧合却又早已注定在解析中的神奇性质。
原作者:亏盈同源不忘初心
修改增添:谭峰
【往期内容】
朋友圈最爆笑的期末考试题,哈哈哈哈
2018上海春考数学试卷
期末考试前,你必须知道一件事
近十七年上海春考试卷下载地址
四校八大自招信息汇总
2018年上海春季高考招生信息汇总
2018上海市高三一模填选难题解析(十个区)
2017年上海市春考与合格考数学试卷
迄今最难的高三一模卷——2018宝山
你要的2018高三一模卷和答案都在这





