z-score会改变数据分布吗

先说结论: z-score 不会 修改原来的数据分布。

这篇是 z-score的标准化究竟怎么弄？ 中如下内容的修订

那么默认参数下，我们就是对矩阵按列进行z-score的标准化。检验标准很简单，计算标准化的数据的均值和标准差，因为z-score的结果就是让数据服从均值为0，标准差为1的正态分布。

里面说z-score的效果是让数据转换成正态分布的说法是不正确的。z-score的效果就是让变换后的数据的均值为0，标准差为1，不会改变原来的数据分布。（每当看到0和1，就不自觉地想到标准正态分布，真是尴尬呀）

当然这篇文章不只是纠正一个错误而已，还想介绍一个除了搜索以外还有什么方法是可以验证自己的想法的方法。这个方法很简单，就是 实践出真知 。

因为我原来的观点是z-score会改变了数据分布，那么最简单的验证方法就是找一个原本不是正态分布的数据做一个z-score变换，观察前后的数据分布即可。而这个可以通过R语言实现。

什么样的分布不是正态分布呢？

x  1:100
y  1:100
mean(y) # 50.5
sd(y) # 29.01149
plot(x,y, pch=".")

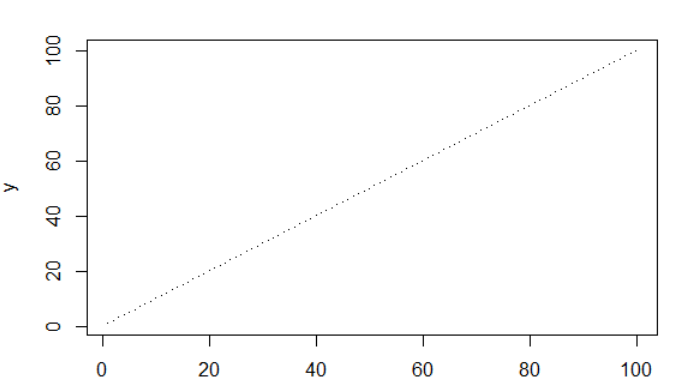
嗯，这个肯定不是正态分布！

之后，我们将y进行z-score变换，也就是 scale 一下

y.s  scale(y)
mean(y.s) # 0
sd(y.s) # 1
plot(x,y.s, pch=".")

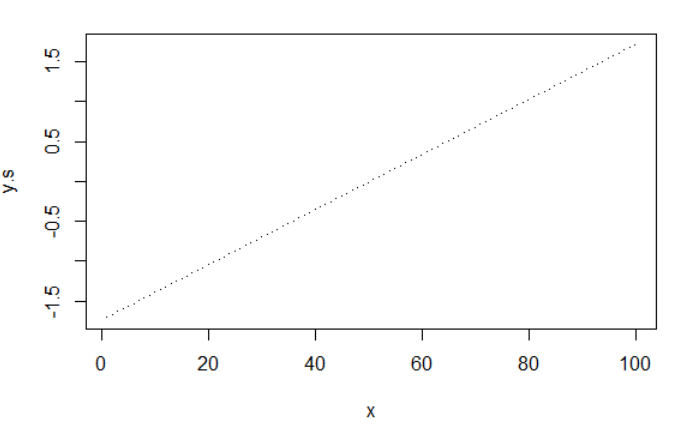
原来是什么分布，z-score变换之后还是原来的分布。因为z-score做的事情是将数据整体偏移（减法）保证了均值为0，随后进行压缩（除法），保证了方差为1。

最后说一句: 尽管我们可以通过学习别人的经验来获取知识，但网络上的资料未必都非常优秀（包括我的），有一些内容是笔误，有一些内容是作者没有搞清楚就写，因此，有些时候你还需要通过自己实践才行。