士兵们,在远方金字塔的顶上,四千年的岁月在俯视你们!
——拿破仑, 1798 年 7 月 21 日在埃及
1858 年,苏格兰律师兼文物收藏家莱因德
(A. Remy Rhind, 1833
一 1863)
在前往尼罗河谷的旅途中买了一份文献,这份文献是几年前在上埃及底比斯城(现在的卢克索附近)的一个小建筑废墟中出土的。这份文献现在被称为《莱因德纸草书》(Rhind Papyrus), 是一本包含84 个数学问题的文集,内容涉及算术、早期代数和几何
[1]
。由于莱因德 30 岁时英年早逝,这批文献随后为大英博物馆所拥有,成为永久馆藏。这份纸草书最初被发现时是 548.6厘米长、33.02厘米宽的卷轴,但是当大英博物馆得到它时,一部分已经遗失。然而,十分幸运的是,后来发现这些遗失的部分由纽约历史协会所保存,因此现在可以看到完整的文献。
古埃及的神殿及宝藏,总是令欧洲的旅行者们神往不已。1799 年拿破仑率领军队入侵埃及,虽然以失败告终,但是却为大批的学者、文物研究者和探险者们打开了通往埃及的大门。拿破仑对文化和科学有着浓厚的兴趣,他的幕僚中有众多各个领域的学者,其中就有数学家傅里叶
(我们在后面还会谈到他)
。这些学者在整个埃及搜罗古代的宝藏,凡是能带走的都带回了欧洲。他们最著名的发现,就是在尼罗河三角洲最西端的小镇拉希德
(欧洲人称之为罗塞塔)
附近发掘出的一块巨大玄武岩石碑。
和莱因德纸草书一样,罗塞塔石碑最后也是由大英博物馆收藏,上面刻有托勒密五世王朝
(公元前 195 年)
由埃及僧侣组成的议会所颁布的一项法令,分别用 3 种文字——希腊文、古埃及通用文字和象形文字写成。英国物理学家托马斯·杨
(Thomas Young, 1773 一 1829)
是第一个破译出石碑上文字的人
(托马斯兴趣广泛,最著名的成就是他关于光的波理论)
。通过比较 3 种文字中相似符号的重复部分,他能够编纂出一部关于古埃及文字的初级字典。这部字典最后于 1822 年由法国著名的埃及古物学者商博良
(1790 一 1832)
完成,商博良还在刻文中辨识出了埃及艳后克利奥帕特拉的名字。商博良具有划时代意义的工作,使得学者们得以译出大量写在莎草纸、木片以及石碑上的古埃及文献,其中就有几卷是有关数学的文献。最长最完整的数学文献是莱因德纸草书。
德国学者埃森洛尔最先将莱因德纸草书翻译成现代语言,英译版则由皮特所译, 1923 年在伦敦出版
[2]
。但是影响最广泛的版本则是由蔡斯于 1929 年完成的。蔡斯原本是一个美国商人, 1910 年的埃及之行使他成
为一位埃及古物学者。正是通过他的版本,莱因德纸草书才被普通大众所知道。
[3]
纸草书上的文字是用僧侣体从右向左写成的,这与较早的象形文字截然相反。全文用黑红两种颜色写成,并配有几何图形。它是由一位名叫
阿莫斯
的书吏所写下的,现代的作者一般称他为
阿梅斯
。但是纸草书上所记载的内容不是他自己的著作,他只是将它们从更古老的手稿中抄录下来而已,这可以从他自己的序文中看出:
本书是在第 33 年洪水泛滥季节的第四个月所抄录的,时值上下埃及统治者阿屋赛瑞法老时代,它以相似的形式,为上下
埃及统治者奈马特瑞时代的文献赋予新的生命。抄录者是阿梅斯。
[4]
上面提到的第一位法老阿屋赛瑞,已经确认是希克索斯王朝的君王之一,大约生活在公元前 1650 年左右。第二位法老奈马特瑞是阿美尼赫特三世,统治时期是公元前 1849 年至公元前 1801 年,这一时期被称为中王国时代。因此我们可以确定出原著和抄录的确切时间,
这份文献写于将近四千年前,是目前所知年代最早、内容最广泛的古代数学文献
之一。
[5]
这本著作在一开始就展现了作者的宏大愿景:计划向读者提供一个
“对所有事物全面而彻底的研究,洞察所有存在的事物,知晓所有的秘密”
[6]
。即使这些愿望未能很好地实现,这本著作仍然使我们能够对古埃及数学有非常深刻的领悟。文献中所列出的 84 个问题涵盖算术、口述代数
(求出未知量)
、测量
(面积和体积计算)
,甚至还有等差及等比数列。那些习惯于希腊数学形式结构
(定义、公理、定理和证明)
的人,一定会对莱因德纸草书的内容感到失望,因为这里既没有提出可以应用到某一类问题上的一般规则,也没有根据先前事实逻辑推导出来的结果。相反,问题都是给出特定值的特定例子。它们几乎都是“叙述型问题“,处理的都是很平凡的事物,比如求出一块田地的面积,一个粮仓的容积,或者是如何在许多人当中分配一定数量的面包等。显然,这本著作是书吏学校的一本习题集,因为当时只有皇室书吏阶级才能从事文字工作,包括阅读、书写和算术,也就是我们现在的“3R”
[7]
。该纸草书还包含了一个看上去没有实际用途的问题,其目的显然是挑战和娱乐读者
(见本章后的“古埃及的数学娱乐”)。
莱因德纸草书的开头是两个表:一个是 2 被 3 到 101 之间所有奇数除的
除法表,另一个则是整数 1 到 9 被 10 除的除法表。所有答案都是以单位分数
(分子是 1 的分数)
的形式给出的。不知道是出于什么原因,这是古埃及人所知道的用来处理分数的唯一方式, 2/3 是一个例外,它本身被视作
一个基本的分数。他们花费大量的功夫和技巧将一个分数分解成单位分
数的和。例如, 6 被 10 除的结果是 l/2+1/10, 7 被 10 除的结果是 2/3+ 1/30
[8]
。
当然,古埃及人并没有使用我们现代的符号来表示分数,他们在整数上加一个点
(或者在象形文字上加一个椭圆圈)
来表示该整数的倒数。他们也没有表示加法的符号,单位分数简单地并列写在一起就表示它们相加
[9]
。
该文献接下来处理的是包含减法
(称为“求全”)
和乘法的算术问题,
以及求解未知量的问题。这些问题统称为“啊哈” 问题,因为它们通常以字母 h
(发音 aha 或者 hau)
开头,所代表的意思可能就是要找出的“未知量”
[10]
。例如,第 30 个问题问:“如果问,什么数的 2/3+1/10 是
10, 请告诉他。”文献中记载的答案是 13+1/23, 并且在后面列出一个证
明过程
(我们现今称之为“验证”)
,来证明这确实是一个正确答案。用现代的语言来说,第 30 题等同于解方程
。这类线性方程用所谓的“试位法”来求解:假设用一个合适
(容易算)
的数字表
示
(比如 30)
, 代入到方程中。则等式左边变成 23, 不等于 10。又因为
23 必须乘以 10/23 才能得到 10, 所以正确的解应该是 10/23 乘以假设的值,
也就是 x=300/23=13+1/23。可见,在现代代数符号出现之前约 3 500 年,
埃及人就已经掌握了一种能够有效求解线性方程的方法
[11]
。
第 41 ~ 60 题实质上是几何问题。第 41 题说:“求出一个直径为 9, 高度为 10 的圆柱形粮仓的容积。”解答如下:“减去 9 的 1/9
(也就是 1)
, 得到
8 。将 8 乘以 8, 得到 64。将 64 乘以 10, 得到 640 。”(单位是
立方腕尺
,然后
作者
将此结果乘以 15/2, 转换成“赫卡" ——这是当时用来测量谷物容积的标准单位,1 赫卡等于 4.789立方分米。)
[12]
显然,
为了计算出圆柱的底面积,书吏将圆形的底用边长为直径的 8/9 的正方形
来代替。如果用
来表示直径,则面积公式为
。如果将此公式与
相比较,我们可以发现埃及人使用的
值是
, 这与真实值的误差只有
, 。精确度之高让人惊叹,真是非常了不起的成就!
[13]
我们特别感兴趣的是第 56 题到第 60 题,这几道题都与埃及最著名的名胜古迹金字塔有关,并且所有的问题都用到了单词“塞克特”
(seked,
参见图 1)
[14]
。这个单词的意思我们随后就会知道。
 图 1 莱因德纸草书第56 题
图 1 莱因德纸草书第56 题
第 56 题说:“如果一个金字塔高 250 腕尺,底边的边长 360 腕尺,则它
的‘塞克特’是多少?”阿梅斯的解答如下:
取 360 的 1/2 为 180, 为了得到 180, 乘以 25O, 得到 1/2 1/5 1/50
腕尺。1 腕尺等于 7 掌(palm), 用 7 乘以 1/2 1/5 1/50:
 则塞克特是
掌即
则塞克特是
掌即
让我们来分析一下这个解。显然, 360 的 1/
2 (即 180)
, 是金字塔正方形底边长的一半
(参见图 2)
。”为了得到 180, 乘以 250" 的意思是,找出一个数
使得 250 乘以
等于 180, 因此可得 x=
。但是埃及数学家要求所有的答案都必须以单位分数的形式给出,而 1/2 、1/5 和
1/50 的和正好是 18/25, 所以这个数值是金字塔底边长的一半与金字塔的
高之比,也就是金字塔侧面的横宽对纵高(run-to-rise) 之比。事实上,
阿梅斯发现的这个量
(塞克特)
,就是金字塔的底面与侧面夹角的余切值
[16]
。
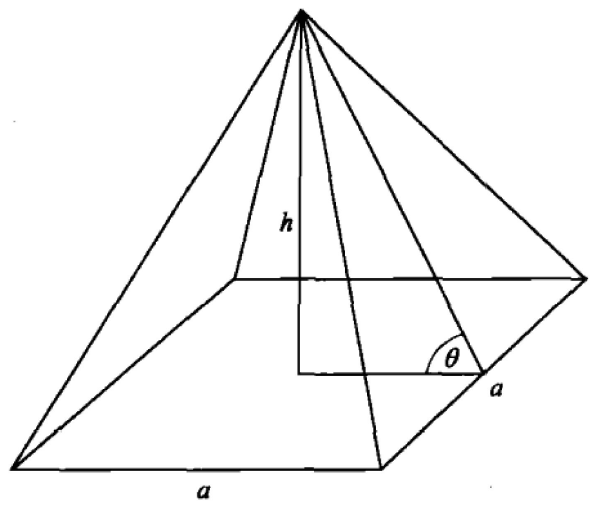 图2 正方形底的金字塔
图2 正方形底的金字塔
有读者可能马上会产生两个疑问。首先,为什么他不像我们今天的做法一样求出这个比率的倒数,也就是纵高对横宽之比呢?答案是,人
们在建造垂直建筑物时,会很自然地去度量当高度增加一单位时,水平方向与垂线的偏离程度,也就是横宽对纵高之比。这确实是建筑学的实际做法,他们用“直倾斜”(batter) 来度量一面想象中的竖直墙的内倾斜率。
其次,为什么阿梅斯要把他的答案乘以 7 呢?其原因是,金字塔的建造者们在测量水平距离时常用“掌”或者“手”作为单位,而测量垂直距离则用腕尺作为单位。1 腕尺等于 7 掌,因此所求出的“塞克特”值
是以每腕尺的“掌数”为单位给出的横宽对纵高之比。当然,我们今天 25 只是将这些比率视作纯数字。
为什么横宽对纵高之比被认为如此重要,以至于被赋予一个专有名词,并且在纸草书中占用了四个题目?原因在于,金字塔建造者必须保持每个面相对水平面的倾斜度是一致的。这可能在纸上看着非常容易,
但是一旦开始实际建造,建筑工人就必须经常检查他们的进度,以确保在施工过程中保持所需的倾斜度。也就是说,每一个面的“塞克特”值必须一样。
第 51 题是第 56 题的相反问题:给出“塞克特”的值和底边的边长,然后求高。第 58 题和 59 题与 56 题类似,得到“塞克特”的值是
掌
(每腕尺)
,所不同的是,答案以 5 掌 l 指
(finger, 1 掌等于 4 指)
来表示。最后,第 60 题是求一个高 30 腕尺、底 15 腕尺的柱子的“塞克特”值。我们不知道该柱子是金字塔形状,还是圆柱形
(如果是此情形, 15 则是底面的直 径)
。然而不论是哪种情况,答案都是 1/4 。
第 56 题中求出的“塞克特”是 18/25
(无量纲单位)
,对应着底与面的夹角是 54°15' 。第 58 题和 59 题所求出的“塞克特”转换成无量纲单位就是
, 即 3/4, 对应的角是 53°8' 。将这些数字与吉萨的一些金字塔的实际角度相比较,可以得到以下有趣的结果
[17]
。
基奥普斯金字塔:51°52'
切夫伦金字塔:52°20'
迈锡里努斯金字塔:50°47'
这些数字与例题中算出的结果非常接近。至于第 60 题中的柱子,它
的角度则大多了,当然也和我们对这种建筑的预期相吻合:
。













