微信昵称为“Zach”的读者朋友问到下面的问题:
左老师,这道题看了解析以后总觉得怪怪的,但是又没有强有力的证据支持我的想法,所以想问问您 .

这道题有三点疑惑.
第(1)处那里,它是同时用了两个基本不等式.
请问,这里满足基本不等式中的“正、定、等”吗?
不是说相加或相乘要为定值吗?但(2x-1)*1也不为定值啊.
第(2)处那里.即便第(1)处没有问题,在连用两个基本不等式之后,已经是前一个式子的最小值,这里又再用一次基本不等式求最小值的最小值,合理吗?
第(3)处,因为用了三次基本不等式.当然要有三个当且仅当.
但是,如果这里三个等式不能同时取等号又该怎么做?(当然这道题可以,有没有可能无法同时取等的时候).
最后,有没有别的易于理解的解法?
谢谢.
Zach,
你应该是认真看过了互动的正确姿势,问的很具体,这才是合适的提问方法.
这样我们的沟通效率才高.
为什么求最值一定要“定”?
童鞋们都知道,用基本不等式求最值的三字诀——一正二定三相等.
市面上的资料基本围绕如何满足“一正二定三相等”的条件来求最值.
但是却很少讲,为什么一定要这三个条件呢?
“正”字不必多说,大家好理解,这是推导基本不等式的前提条件.
再来看“定”:a*b为定值,则a+b有最小值;a+b为定值,则a*b有最大值.即“积定和最小,和定积最大”.
为什么一定要“定值”呢?
看栗子.

这样解虽然使用了基本不等式,但是右边的式子并不是定值,结果正确吗?
显然,当x=2时,(9-2x)x的值等于10>9,所以上面的解法错误.
错误是如何发生的呢?
我们分别画出两个函数f(x)=(9-2x)x,g(x)=[(9-x)/2]^2的图象.
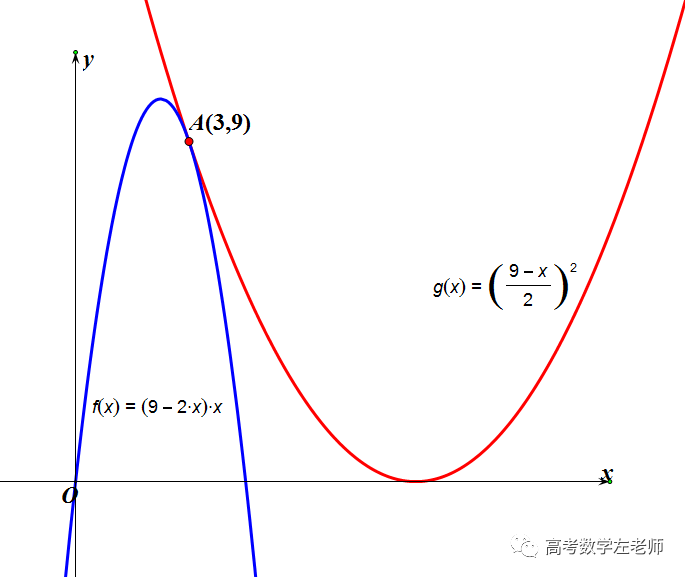
从上图我们能看出:随着x的变化,(9-2x)x、[(9-x)/2]^2也都在变化,而且(9-2x)x始终小于等于[(9-x)/2]^2.
而且,当9-2x=x即x=3时,(9-2x)x等于[(9-x)/2]^2.
这些都没有错.
但是来了.
但是取等号时的位置并不是取最值的位置.
怎样能保证取等号时就是最值呢?
答案是:必须定值!
看正确解法.

再看图象,我们画出函数两个函数f(x)=(9-2x)x,g(x)=81/8的图象.
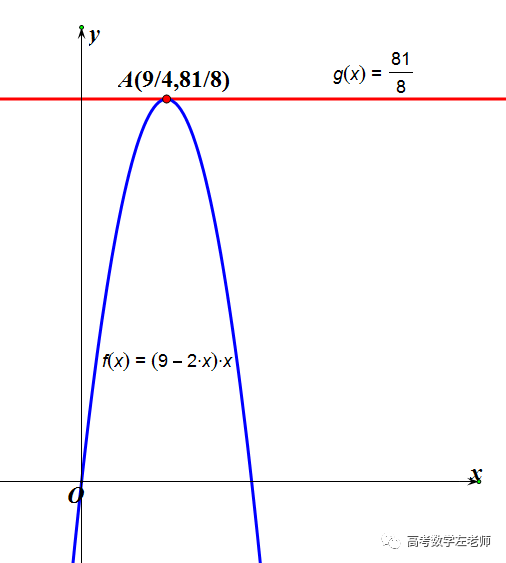
看出定值的好处来了吗?
因为是定值,它的图象是一条平行于x轴的直线,这样就保证了——f(x)的图象都在直线的下方,取等号的位置就是最值的问题.
最后就到了“等”的要求了.
无需多言,如果等号取不到,最值显然也取不到.
可以多步到达“定”,只要多个等号能同时取得
从上面的分析我们能看出,用基本不等式求最值不仅要求“一正二定三相等”,而且顺序都不能变——先要求"正",再要求"定",最后研究取等的条件是否满足.
当然,如果只是使用基本不等式研究两个变量的不等关系,只要明白“正”和“相等”就够了.
比如,我们只是比较0
首先确定是否为正数.
然后使用基本不等式,知道(9-2x)x<=(9-x)^2/4.
最后我们确定,当9-2x=x即x=3时,二者相等.
这就为“定值”提供了另外一种路径——多步到达“定值”.

画出图来,是这样的感觉.
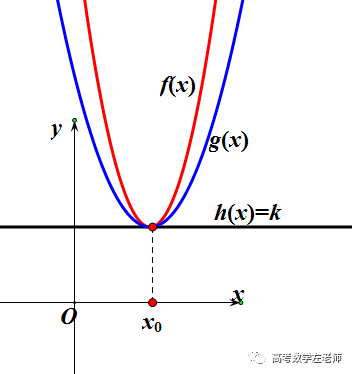
只要中间的两个等号能够同时取得,f(x)也能取得最小值.
所以,你提供的答案解析是可行的.
回到你的问题:如果中间的几个等号不能同时取得,怎么办?
那就说明,这个解法行不通,要换别的思路.
画出图来,就类似于这样.
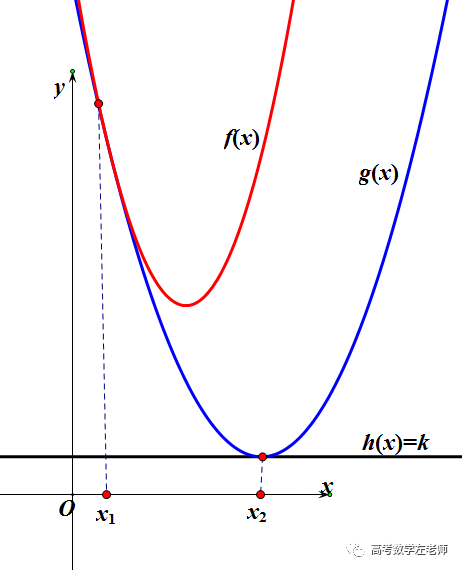
从上图看出,两个取等条件不一致,所以最终取不到最值.
有无其它解法?
你问是否有易于理解的解法?
我想,你的意思是问,有没有一步到位的解法?
也有,但同时需要学一点基本不等式的拓展——从二元到多元.

上面的解法中,用到了四元的基本不等式.
实际上,基本不等式可拓展到n元.学霸筒子们可参考.
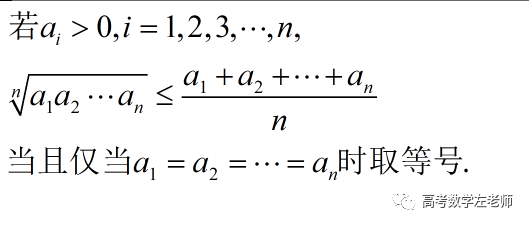
温馨提示:要获取微信公众号“高考数学左老师”的精华内容,可以回复“关键词”,你会获得一份关键词列表.根据这份列表,回复对应的关键词,就可获得内容.
推荐阅读:圆锥曲线综合题之定值问题
上一篇:二面角的平面角如何确定是锐角还是钝角?
--END--
苹果手机用户专属赞赏二维码






