【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第10章 人工神经网络介绍（中）

作者：ApacheCN【翻译】   Python机器学习爱好者
Python爱好者社区专栏作者
GitHub：https://github.com/apachecn/hands_on_Ml_with_Sklearn_and_TF

前文传送门：

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— Chapter 0.前言

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第1章 机器学习概览（上）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第1章 机器学习概览（下）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第2章  一个完整的机器学习项目（上）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第2章 一个完整的机器学习项目（中）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第2章 一个完整的机器学习项目（中二）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第2章 一个完整的机器学习项目（下）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第3章 分类（上）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第3章 分类（中）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第3章 分类（下）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第4章( 上） 训练模型

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第4章( 中） 训练模型

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第4章( 下） 训练模型

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第5章( 上）支持向量机

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第5章( 中）支持向量机

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第5章( 中）支持向量机

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第5章( 下）支持向量机

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第6章 决策树

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第7章 集成学习和随机森林（上）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第7章 集成学习和随机森林 （中）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第7章 集成学习和随机森林 （下）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第8章 降维（上）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第8章 降维（下）

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 ——  第9章 （上）启动并运行TensorFlow

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第9章 （中）启动并运行TensorFlow

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第9章 （下）启动并运行TensorFlow

【翻译】Sklearn 与 TensorFlow 机器学习实用指南 —— 第10章 人工神经网络介绍（上）

多层感知器与反向传播

MLP 由一个（通过）输入层、一个或多个称为隐藏层的 LTU 组成，一个最终层 LTU 称为输出层（见图 10-7）。除了输出层之外的每一层包括偏置神经元，并且全连接到下一层。当人工神经网络有两个或多个隐含层时，称为深度神经网络（DNN）。

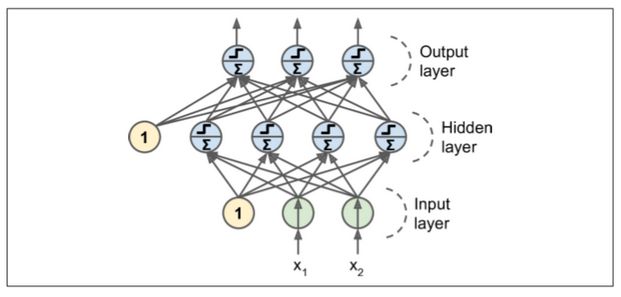
多年来，研究人员努力寻找一种训练 MLP 的方法，但没有成功。但在 1986，D. E. Rumelhart 等人提出了反向传播训练算法。第 9 章我们将其描述为使用反向自动微分的梯度下降（第 4 章讨论了梯度下降，第 9 章讨论了自动微分）。

对于每个训练实例，算法将其馈送到网络并计算每个连续层中的每个神经元的输出（这是向前传递，就像在进行预测时一样）。然后，它测量网络的输出误差（即，期望输出和网络实际输出之间的差值），并且计算最后隐藏层中的每个神经元对每个输出神经元的误差贡献多少。然后，继续测量这些误差贡献有多少来自先前隐藏层中的每个神经元等等，直到算法到达输入层。该反向通过有效地测量网络中所有连接权重的误差梯度，通过在网络中向后传播误差梯度（也是该算法的名称）。如果你查看一下附录 D 中的反向自动微分算法，你会发现反向传播的正向和反向通过简单地执行反向自动微分。反向传播算法的最后一步是使用较早测量的误差梯度对网络中的所有连接权值进行梯度下降步骤。

让我们更简短一些：对于每个训练实例，反向传播算法首先进行预测（前向），测量误差，然后反向遍历每个层来测量每个连接（反向传递）的误差贡献，最后稍微调整连接器权值以减少误差（梯度下降步长）。

为了使算法能够正常工作，作者对 MLP 的体系结构进行了一个关键性的改变：用 Logistic 函数代替了阶跃函数， σ(z) = 1 / (1 + exp(–z)) 。这是必要的，因为阶跃函数只包含平坦的段，因此没有梯度来工作（梯度下降不能在平面上移动），而 Logistic 函数到处都有一个定义良好的非零导数，允许梯度下降在每个步上取得一些进展。反向传播算法可以与其他激活函数一起使用，而不是 Logistic 函数。另外两个流行的激活函数是：

• 双曲正切函数 tanh (z) = 2σ(2z) – 1

• 就像 Logistic 函数，它是 S 形的、连续的、可微的，但是它的输出值范围从-1到1（不是在 Logistic 函数的 0 到 1），这往往使每个层的输出在训练开始时或多或少都正则化了（即以 0 为中心）。这常常有助于加快收敛速度。

• Relu 函数（在第 9 章中介绍）

• ReLU (z) = max (0, z) 。它是连续的，但不幸的是在 z=0 时不可微（斜率突然改变，这可以使梯度下降反弹）。然而，在实践中，它工作得很好，并且具有快速计算的优点。最重要的是，它没有最大输出值的事实也有助于减少梯度下降期间的一些问题（我们将在第 11 章中回顾这一点）。

这些流行的激活函数及其衍生物如图 10-8 所示。

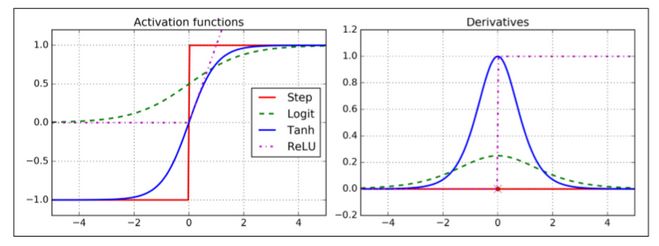
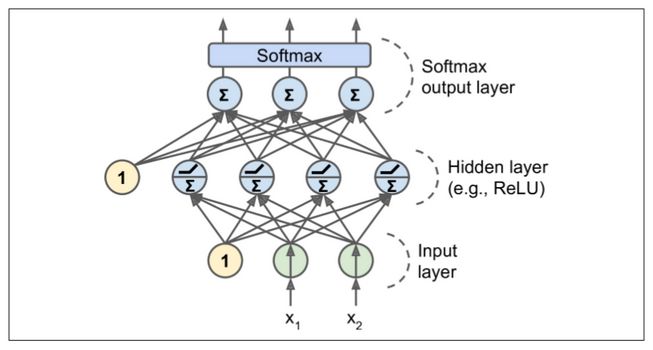
MLP 通常用于分类，每个输出对应于不同的二进制类（例如，垃圾邮件/正常邮件，紧急/非紧急，等等）。当类是多类的（例如，0 到 9 的数字图像分类）时，输出层通常通过用共享的 softmax 函数替换单独的激活函数来修改（见图 10-9）。第 3 章介绍了 softmax 函数。每个神经元的输出对应于相应类的估计概率。注意，信号只在一个方向上流动（从输入到输出），因此这种结构是前馈神经网络（FNN）的一个例子。

生物神经元似乎是用 sigmoid（S 型）激活函数活动的，因此研究人员在很长一段时间内坚持 sigmoid 函数。但事实证明，Relu 激活函数通常在 ANN 工作得更好。这是生物研究误导的例子之一。

用 TensorFlow 高级 API 训练 MLP

与 TensorFlow 一起训练 MLP 最简单的方法是使用高级 API TF.Learn，这与 sklearn 的 API 非常相似。 DNNClassifier 可以很容易训练具有任意数量隐层的深度神经网络，而 softmax 输出层输出估计的类概率。例如，下面的代码训练两个隐藏层的 DNN（一个具有 300 个神经元，另一个具有 100 个神经元）和一个具有 10 个神经元的 SOFTMax 输出层进行分类：

import tensorflow as tf
feature_columns = tf.contrib.learn.infer_real_valued_columns_from_input(X_train) dnn_clf = tf.contrib.learn.DNNClassifier(hidden_units=[300, 100], n_classes=10,                                         feature_columns=feature_columns) 
dnn_clf.fit(x=X_train, y=y_train, batch_size=50, steps=40000) 

如果你在 MNIST 数据集上运行这个代码（在缩放它之后，例如，通过使用 skLearn 的 StandardScaler ），你实际上可以得到一个在测试集上达到 98.1% 以上精度的模型！这比我们在第 3 章中训练的最好的模型都要好：

>>> from sklearn.metrics import accuracy_score 
>>> y_pred = list(dnn_clf.predict(X_test)) 
>>> accuracy_score(y_test, y_pred) 
0.98180000000000001 

TF.Learn 学习库也为评估模型提供了一些方便的功能：

>>> dnn_clf.evaluate(X_test, y_test) 
{'accuracy': 0.98180002, 'global_step': 40000, 'loss': 0.073678359} 

DNNClassifier 基于 Relu 激活函数创建所有神经元层（我们可以通过设置超参数 activation_fn 来改变激活函数）。输出层基于 SoftMax 函数，损失函数是交叉熵（在第 4 章中介绍）。

TF.EXCEL API 仍然是更新的，所以在这些例子中使用的一些名称和函数可能会在你读这本书的时候发生一些变化。但总的思想是不变。

使用普通 TensorFlow 训练 DNN

如果您想要更好地控制网络架构，您可能更喜欢使用 TensorFlow 的较低级别的 Python API（在第 9 章中介绍）。 在本节中，我们将使用与之前的 API 相同的模型，我们将实施 Minibatch 梯度下降来在 MNIST 数据集上进行训练。 第一步是建设阶段，构建 TensorFlow 图。 第二步是执行阶段，您实际运行计算图谱来训练模型。

构造阶段

开始吧。 首先我们需要导入 tensorflow 库。 然后我们必须指定输入和输出的数量，并设置每个层中隐藏的神经元数量：

import tensorflow as tf
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10

接下来，与第 9 章一样，您可以使用占位符节点来表示训练数据和目标。 X 的形状仅有部分被定义。 我们知道它将是一个 2D 张量（即一个矩阵），沿着第一个维度的实例和第二个维度的特征，我们知道特征的数量将是 28×28 （每像素一个特征） 但是我们不知道每个训练批次将包含多少个实例。 所以 X 的形状是 (None, n_inputs) 。 同样，我们知道 y 将是一个 1D 张量，每个实例有一个入口，但是我们再次不知道在这一点上训练批次的大小，所以形状 (None) 。

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")

现在让我们创建一个实际的神经网络。 占位符 X 将作为输入层; 在执行阶段，它将一次更换一个训练批次（注意训练批中的所有实例将由神经网络同时处理）。 现在您需要创建两个隐藏层和输出层。 两个隐藏的层几乎相同：它们只是它们所连接的输入和它们包含的神经元的数量不同。 输出层也非常相似，但它使用 softmax 激活函数而不是 ReLU 激活函数。 所以让我们创建一个 neuron_layer() 函数，我们将一次创建一个图层。 它将需要参数来指定输入，神经元数量，激活函数和图层的名称：

def neuron_layer(X, n_neurons, name, activation=None):
    with tf.name_scope(name):
        n_inputs = int(X.get_shape()[1])
        stddev = 2 / np.sqrt(n_inputs)
        init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
        W = tf.Variable(init, name="weights")
        b = tf.Variable(tf.zeros([n_neurons]), name="biases")
        z = tf.matmul(X, W) + b
        if activation == "relu":
            return tf.nn.relu(z)
        else:
            return z

我们逐行浏览这个代码：

1. 首先，我们使用名称范围来创建每层的名称：它将包含该神经元层的所有计算节点。 这是可选的，但如果节点组织良好，则 TensorBoard 图形将会更加出色。

2. 接下来，我们通过查找输入矩阵的形状并获得第二个维度的大小来获得输入数量（第一个维度用于实例）。

3. 接下来的三行创建一个保存权重矩阵的 W 变量。 它将是包含每个输入和每个神经元之间的所有连接权重的2D张量；因此，它的形状将是 (n_inputs, n_neurons) 。它将被随机初始化，使用具有标准差为 2/√n 的截断的正态（高斯）分布(使用截断的正态分布而不是常规正态分布确保不会有任何大的权重，这可能会减慢训练。).使用这个特定的标准差有助于算法的收敛速度更快（我们将在第11章中进一步讨论这一点），这是对神经网络的微小调整之一，对它们的效率产生了巨大的影响）。 重要的是为所有隐藏层随机初始化连接权重，以避免梯度下降算法无法中断的任何对称性。（例如，如果将所有权重设置为 0，则所有神经元将输出 0，并且给定隐藏层中的所有神经元的误差梯度将相同。 然后，梯度下降步骤将在每个层中以相同的方式更新所有权重，因此它们将保持相等。 换句话说，尽管每层有数百个神经元，你的模型就像每层只有一个神经元一样。）

4. 下一行创建一个偏差的 b 变量，初始化为 0（在这种情况下无对称问题），每个神经元有一个偏置参数。

5. 然后我们创建一个子图来计算 z = X·W + b 。 该向量化实现将有效地计算输入的加权和加上层中每个神经元的偏置，对于批次中的所有实例，仅需一次.

6. 最后，如果激活参数设置为 relu ，则代码返回 relu(z) （即 max(0,z) ），否则它只返回 z 。

好了，现在你有一个很好的函数来创建一个神经元层。 让我们用它来创建深层神经网络！ 第一个隐藏层以 X 为输入。 第二个将第一个隐藏层的输出作为其输入。 最后，输出层将第二个隐藏层的输出作为其输入。

    with tf.name_scope("dnn"):
        hidden1 = neuron_layer(X, n_hidden1, "hidden1", activation="relu")
    hidden2 = neuron_layer(hidden1, n_hidden2, "hidden2", activation="relu")
    logits = neuron_layer(hidden2, n_outputs, "outputs")

请注意，为了清楚起见，我们再次使用名称范围。 还要注意，logit 是在通过 softmax 激活函数之前神经网络的输出：为了优化，我们稍后将处理 softmax 计算。

正如你所期望的，TensorFlow 有许多方便的功能来创建标准的神经网络层，所以通常不需要像我们刚才那样定义你自己的 neuron_layer() 函数。 例如，TensorFlow 的 fully_connected() 函数创建一个完全连接的层，其中所有输入都连接到图层中的所有神经元。 它使用正确的初始化策略来负责创建权重和偏置变量，并且默认情况下使用 ReLU 激活函数（我们可以使用 activate_fn 参数来更改它）。 正如我们将在第 11 章中看到的，它还支持正则化和归一化参数。 我们来调整上面的代码来使用 fully_connected() 函数，而不是我们的 neuron_layer() 函数。 只需导入该功能，并使用以下代码替换 dnn 构建部分：

    from tensorflow.contrib.layers import fully_connected
    with tf.name_scope("dnn"):
        hidden1 = fully_connected(X, n_hidden1, scope="hidden1")
        hidden2 = fully_connected(hidden1, n_hidden2, scope="hidden2")
        logits = fully_connected(hidden2, n_outputs, scope="outputs",
                                    activation_fn=None)

tensorflow.contrib 包包含许多有用的功能，但它是一个尚未分级成为主要 TensorFlow API 一部分的实验代码的地方。 因此， full_connected() 函数（和任何其他 contrib 代码）可能会在将来更改或移动。

使用 dense() 代替 neuron_layer()




注意：本书使用 tensorflow.contrib.layers.fully_connected() 而不是 tf.layers.dense() （本章编写时不存在）。

现在最好使用 tf.layers.dense() ，因为 contrib 模块中的任何内容可能会更改或删除，恕不另行通知。 dense() 函数与 fully_connected() 函数几乎相同，除了一些细微的差别：

几个参数被重命名： scope 变为名称， activation_fn 变为激活（同样 _fn 后缀从其他参数（如 normalizer_fn ）中删除）， weights_initializer 成为 kernel_initializer 等。默认激活现在是无，而不是 tf.nn.relu 。 第 11 章还介绍了更多的差异。

with tf.name_scope("dnn"):
    hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
                              activation=tf.nn.relu)
    hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
                              activation=tf.nn.relu)
    logits = tf.layers.dense(hidden2, n_outputs, name="outputs")

现在我们已经有了神经网络模型，我们需要定义我们用来训练的损失函数。 正如我们在第 4 章中对 Softmax 回归所做的那样，我们将使用交叉熵。 正如我们之前讨论的，交叉熵将惩罚估计目标类的概率较低的模型。 TensorFlow 提供了几种计算交叉熵的功能。 我们将使用 sparse_softmax_cross_entropy_with_logits() ：它根据“logit”计算交叉熵（即，在通过 softmax 激活函数之前的网络输出），并且期望以 0 到 -1 数量的整数形式的标签（在我们的例子中，从 0 到 9）。 这将给我们一个包含每个实例的交叉熵的 1D 张量。 然后，我们可以使用 TensorFlow 的 reduce_mean() 函数来计算所有实例的平均交叉熵。

with tf.name_scope("loss"):
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")

该 sparse_softmax_cross_entropy_with_logits() 函数等同于应用 SOFTMAX 激活函数，然后计算交叉熵，但它更高效，它妥善照顾的边界情况下，比如 logits 等于 0，这就是为什么我们没有较早的应用 SOFTMAX 激活函数。 还有称为 softmax_cross_entropy_with_logits() 的另一个函数，该函数在标签单热载体的形式（而不是整数 0 至类的数目减 1）。

我们有神经网络模型，我们有损失函数，现在我们需要定义一个 GradientDescentOptimizer 来调整模型参数以最小化损失函数。没什么新鲜的; 就像我们在第 9 章中所做的那样：

learning_rate = 0.01

with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)

建模阶段的最后一个重要步骤是指定如何评估模型。 我们将简单地将精度用作我们的绩效指标。 首先，对于每个实例，通过检查最高 logit 是否对应于目标类别来确定神经网络的预测是否正确。 为此，您可以使用