本文获授权转载自微信公众号：无忧公主的数学时间（ID：wuyoushuxue），这是一个六年级小女生无忧公主的数学世界。在公众号里，公主坚持每天一道难题，坚持写原创文章，一年半的时间里发布了500多道题，100多篇原创专栏文章。《棋盘上的“马步”探究》是今年年初时，作为上海业余数学学校的寒假作业而写的一篇探究性论文，刚刚获得了“上海市中学生数学探究性论文”的九年级组一等奖。论文以中国象棋棋盘中“马走日字”为思考点，提出了五个与之相关的数学问题进行探究、推广，非常棒的一篇探究性论文，分享给大家。（如需转载请联系原作者）
0. 问题背景 （本课题为九年级组探究课题）
在中国象棋中，马的走法是一直一斜，棋谚“马走日字”（本质上说，“马走日字”是走1×2 矩形的对角线）。从棋盘上任意一点出发，马能跳到任意的一个点。
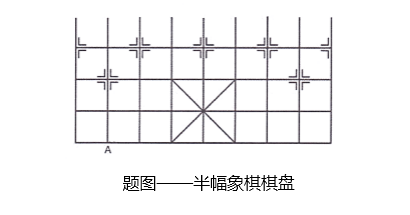
1. 在图中半幅棋盘上，马从点A出发，能否跳到任意的一个点？
分析与解答
我们将半幅棋盘的格点，抽象为5×9的方格矩阵，矩阵中的方格代表棋盘中的一个点。马走“日”字相当于在矩阵中移动时，每一步的行号加减1且列号加减2，或者行号加减2且列号加减1。如果不考虑棋盘的边界问题，每一步一共8种可能移动的方法。原题中的A点，就对应于矩阵中第5行第2列的位置。
为了解答这一题，我构造出了一条遍历矩阵中所有方格的路径，如下图所示。起点为左上角，标号为1，每走一步标号增加1。这样路径轨迹上的标号，就形成了一个从1到45的序列。图中标出了标号1到7的移动方向，作为示例。点A所在的方格，即图中标号32的位置，也显然在这条路径上。从A出发，沿着这条路径，不仅可以到达棋盘中的任意点，而且路径上的方格也不会重复走到。
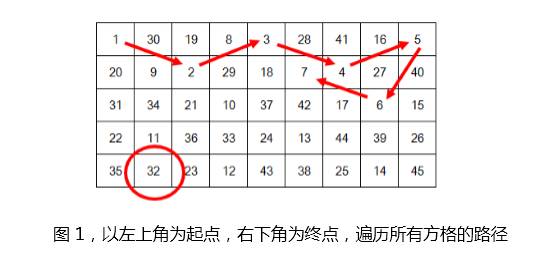
因此，马从A点出发，是可以跳到半幅棋盘上的任意一点的。
另一种解法
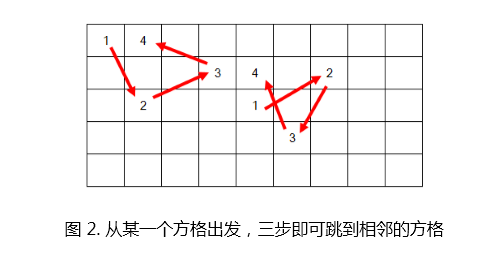
这个问题的上述解法，是基于构造完成的，即构造出了一条遍历所有节点的遍历路径。每个点只走一次的路径，也叫做哈密尔顿路径。我认为还有另一个解法可以讨论。如下图所示，从某一个节点出发，只需要跳 3 步，即可到达相邻的位置。图中给出了以左上角和中心点这两个格子为起点的走法。这个操作所需的最大空间为3×4，所以半幅棋盘的空间足够让马跳到相邻的格子上。因此可以证明从任意方格出发，都可以在3步后到达相邻的位置。那么经过拓展，自然也就可以从任意方格出发，经过有限步，构造出一系列相邻的方格为路径，到达任意目标方格。所以起点为A时一定也能做得到，是这个结论的一个特例。
2. 在图中半幅棋盘上，马从点A出发，能否跳遍半个棋盘，且每个点恰都只走到一次？
分析与解答
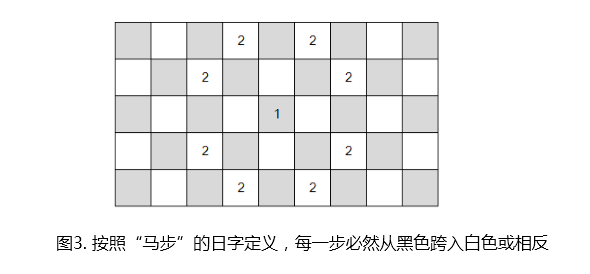
如下图所示，我们将矩阵划分为黑白间隔的样式。马每走一步，必然会跳到一个异色的方格，即从黑色的跳到白色的，或是相反。因此，马跳过的任何一条路径，必然是由黑白间隔的方格组成的序列。如果从任意白色方格出发，且途中每个方格只能经过一次，则整条线路上白色方格的数量必须等于黑色方格的数量，或者比黑色方格的数量大1。而半幅棋盘，总共有45个方格，其中黑色方格为23个，白色方格为22个。因此，从任意白色方格出发，包括A点，不重复地遍历整个棋盘是不可能的。
3. 半幅棋盘上，从哪些点出发，能跳遍半个棋盘，且每个点都只跳一次？
分析与解答
如上题解答中的分析，从任何白色方格出发，都不可能不重复地遍历整个棋盘。而从任意黑色方格出发，遍历整个棋盘，每个方格只走到一次，是可能的。接下来，我们要证明这不仅是可能的，而且确实有解。如下图所示，棋盘中所有的黑色方格一共有23块，因为对称性，如果以其中用字母标出的这8块方格为起点，可以分别构造出一条哈密尔顿路径，则所有黑色方格都可以作为路径的起点了。
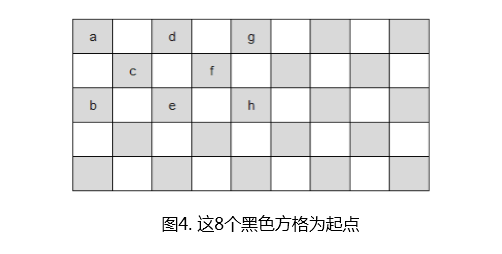
下图给出了以这8个黑色方格为起点的行走方案。所以，以图中任何一个黑色方格为起点，都是存在一条哈密尔顿路径的；而以任何一个白色方格为起点，是不可能做到的。
研究与拓展
上述分析的解法，证明了在5×9的矩阵中，从任何一个黑色格子出发，都存在一条哈密尔顿路径。现在我做一个扩展：基于5×9的哈密尔顿路径，可以扩展到无穷平面空间。也就是说，在无穷大的平面中，都存在一个哈密尔顿路径。
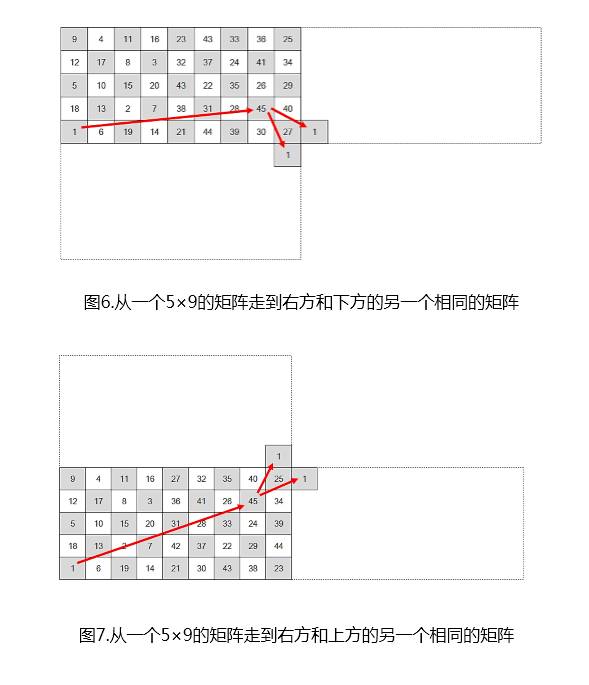
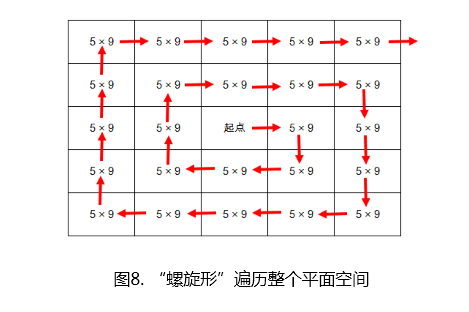
如上面的图6和图7所示，我们构造一条路径，从一个5×9的顶点位置（左下角）可以走到这个矩阵的上、下和右方的同样一个5×9矩阵的顶点位置。这样如果我们把一个平面空间抽象为无数个5×9 的矩阵平铺而成的话，那么就可以从一个顶点出发，采用“螺旋形”的走法，去遍历所有的5×9矩阵。如下图所示，如此走法，就可以构造出在无穷大的平面空间内的一条哈密尔顿路径，即遍历所有的方格，每个方格只走一次。
4. 一个走“目”的“千里马”在整幅棋盘上，能否从任意一点，跳到指定点？
分析与解答
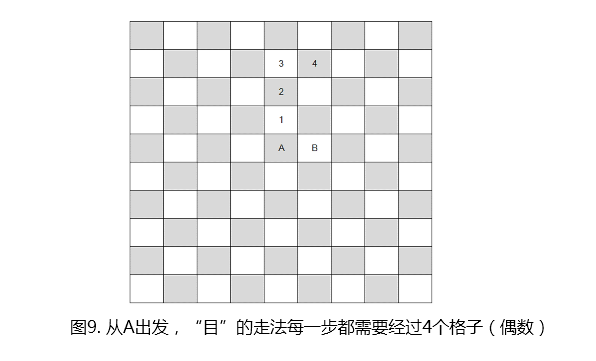
如上图所示，我们假设“千里马”是一只虫子，每次走一个“目”字，都需要爬过4个格子，即从A向一个方向走3格，转90°再走1格。这样，从A出发的任何路径上的每一个能走到的点，距离A的“距离”（即经过的格子数）都是4的倍数，即一个偶数。而从黑色格子（A）出发，终点为白色格子（B），必然需要经过奇数个格子。因此，走“目”字的千里马，从A走到B是不可能的，并且这和棋盘的大小无关。
另一种解法
上述结论还有另一个解法，也比较容易理解。
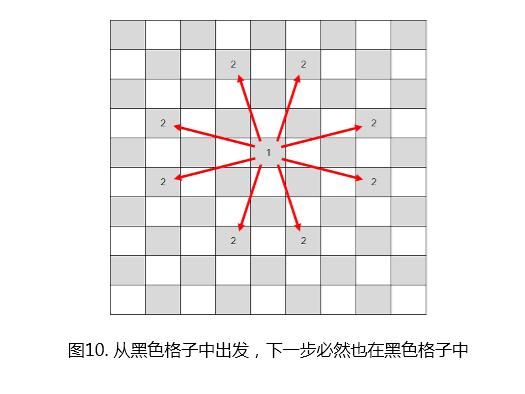
如上图所示，从一个黑色格子出发，下一步必然也在黑色格子中（即必然停留在同色格子内）。因此，无论如何都不可能从黑色格子走到白色格子，反之也一样。
研究与拓展
那么在10×9的整幅棋盘中，从任意一个位置出发，可以跳到的位置的范围是如何的呢？下面我来证明在棋盘中，任意黑色的格子之间可以相互走到，白色的格子之间也可以相互走到。当然，前文已经证明了黑白之间是走不到的。
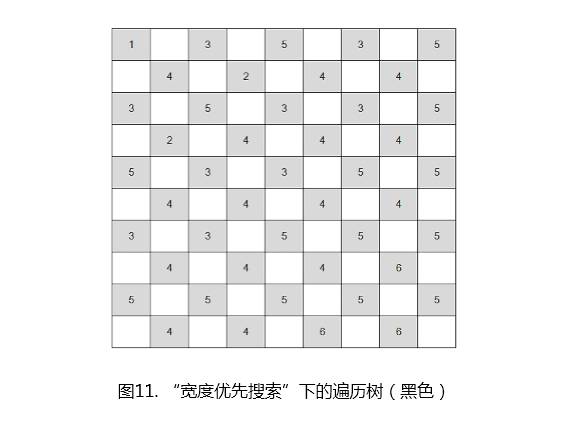
假设左上角的黑色格子为起点，我采用“宽度优先搜索”的算法思想来构造走法。图中左上角标号为1，图中任意标号为i（i > 1）的格子，必然可以找到一个标号为i -1 的格子，通过千里马走到它。实际上标号就表示为从左上角出发，能到达这个格子的最短步数。也就是说，如果从左上角出发，任意黑色格子，最远只需要跳5步（最大标号6减去1）即可到达。
那么从左上角出发，到每一个黑色格子的路径，最终形成了一个树状结构，根节点（出发点）即为左上角的格子。对于任意两个黑色格子，只要从其中一个格子出发，先到达两个黑色格子的公共祖先（共同拥有的上级祖先），当然这里最远可以回到起点，然后再沿路跳转下去就可到达另一个黑色格子。即任意两个黑色格子之间，都存在路径可以到达。
用类似的方法，我们来构造白色格子间的树形结构。
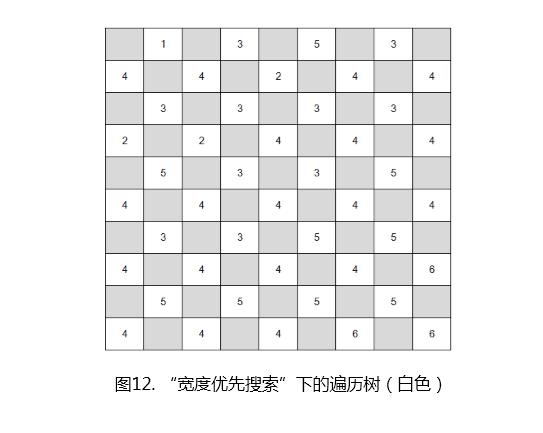
如上图所示，以第一行第二列为起点，遍历结构和前文的黑色格子完全相同。同样方法可以证明，任意白色格子间也可以相互走到。
综上所述，把每个格子看作一个节点，将两两之间能跳到的格子间连边，通过这样的建图的方式，整幅10×9的棋盘的90个节点的图，实际上被构造成了两个互不联通的图。一个由所有黑色格子构成，另一个由白色格子构成，两个图中两两可达（即强连通），但两个图之间没有任何交集。
5. 在一个无限大的棋盘里，有一步能跳“1×n”的“飞马”。怎样的 n（n≥4），能使得它从任意一点出发，能跳到指定点？
分析与解答
我们分两种情况进行分析，讨论n的奇偶性问题。
类似于前文所述的“1×3”的飞马，如果n为奇数，则“1×n”的“飞马，必然只能在同色之间跳转。此时，结论不成立，即不能从任意点出发，跳到任意点，且和棋盘的大小无关。
接下来，我来证明当n为偶数时，必然可以从任意点出发，跳到指定点。
首先，如上图所示，不论n为多少（奇偶不论），从A出发，经过C点后必然可以走到相邻的一个同色的格子。
当n为偶数时，从A出发第一步到达的格子颜色必然和A不同。此时，基于前文的结论，只需要沿着相邻同色的格子走，必然可以达到A相邻的那个异色的格子。如上图所示，B1到B2，一直到Bk。那么如果从任意格子出发，可以经过有限步达到相邻的格子。则沿着相邻的格子逐步迭代，就可以产生一条从A到无限平面中的任意位置的路径了。
综上所述，当n是偶数时，结论成立，即在一个无限大的平面里，飞马从任意一点出发，能跳到指定点。（完）
欢迎大家走进一个六年级小女生的数学世界。>>>无忧公主的123篇原创专栏文章，收藏下来慢慢看哦！
以数学学习为主题，以传播数学文化为己任，以激发学习者学习数学的兴趣为目标，分享有用的数学知识、有趣的数学故事、传奇的数学人物等，为你展现一个有趣、好玩、丰富多彩的数学世界。
