SPSS分析技术：曲线直线化；一氧化碳中毒如何避免？

生活统计学 · 公众号 · · 2017-05-06 00:37

正文

基础准备

前面介绍过，无论是简单线性回归还是多重线性回归，变量之间的线性相关关系是基础，需要注意，这里的相关关系是线性的。

然而很多情况下，变量之间的关系却不是线性的，而是表现为曲线的。通过散点图，我们可以直观的观察变量之间的相关关系如何，左图很明显横轴和纵轴的两个变量之间的相关关系是曲线相关的，而右图的散点图则近似于直线相关。

对于具有曲线相关关系的变量，如果想做回归分析，那么有两条路线可以选择：

曲线直线化，然后用线性回归方法进行；
非线性回归；

SPSS同样提供了这两种曲线回归方法的模块。可以通过【分析】-【回归】-【曲线估算】或【非线性】来选择操作。今天我们介绍SPSS软件中曲线直线化的功能。

SPSS的曲线估算模块

上图是SPSS中曲线估算的模块操作对话框，分析者可以通过这个模块进行曲线直线化，然后再进行数据拟合的过程。在这个对话框中，我们重点强调两点：

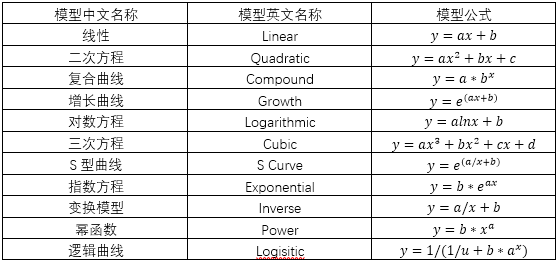
自变量的选择。上方的红框内需要选入的是自变量，这里能够选择的自变量个数只能是一个，也就是说曲线估算（曲线直线化）只提供拟合一个因变量和一个自变量的曲线模型。
曲线直线化模型；SPSS提供的曲线直线化的模型有线性、二次、复合、……、Logistic等11种。这11种曲线模型都能够用于曲线直线化，它们的模型公式为：

曲线直线化

如果面对某些变量的关系是非线性关系（曲线关系）时，最直接的方法就是曲线直线化，曲线直线化的基本原理是将变量进行变换，从而将曲线方程化为直线回归方程进行分析。例如通过散点图观察数据点的分布情况，或者根据前人的文献参考，某个现象的两个变量服从变换模型：

案例分析

近几年经常发生一氧化碳中毒死亡的新闻事件，例如有密闭空间内烧炭自杀和密闭车库开启空调中毒死亡等新闻事件屡见不鲜。很多文献报道过，当空气中的一氧化碳浓度达到3200ppm时，30分钟以内就可以使健康成年人死亡。快速解决高浓度一氧化碳浓度的办法就是通风，因为研究者发现随着通风时间的增加，密闭空间内一氧化碳的浓度会呈指数曲线下降，所以通风的效果是非常显著的。现在有一份一氧化碳浓度随时间下降的数据，用指数方程对该份数据进行拟合。

（例题数据文件已经上传到QQ群，群号请见文章底部温馨提示）

分析思路

本案例中的因变量是一氧化碳浓度，自变量是时间。做回归分析前，首先需要研究一氧化碳浓度与时间的相关关系，可以使用散点图来观察。通过散点图的分布情况，如果是线性关系，则直接使用线性方程拟合，如果是非线性，那就根据散点的分布情况或文献记载，选择合适的曲线直线化模型。如果以上两种方式的效果都不理想，那就采用SPSS的非线性模块，这部分内容会在接下来几天介绍。

分析步骤

制作散点图；

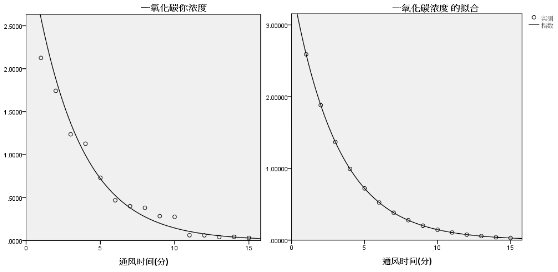
左图为X（通风时间）和Y（一氧化碳浓度）的散点图；右图为X（通风时间）和LnY（Ln一氧化碳浓度）的散点图。明显的，左图的散点图是曲线分布的，而通过指数变换后，散点图则变为直线分布状态了，说明该案例的数据是服从指数方程的。可以表示为：