大年初二话函数思想

微信后台有童鞋问到了这样一道题.

这是浙江省2012年高考数学理科卷第9题.

这使我想说一说，什么是函数的思想.

大家平时经常听老师说，某某题考查了函数与方程的思想，那函数思想到底指什么呢？

通俗地讲，函数思想指的是一种意识，一种解题时的思维习惯，具体说就是用变量和函数的观点来思考问题.

你可以从下面三个层次去体会，在解题时你是否有意识地运用了函数思想？

是不是想到把字母看作变量或把代数式看作函数？

看栗子.

分析：根据离心率e=c/a,我们能用关于a的式子来表示离心率e.

把看到的字母当做变量，把看到的代数式看作关于变量的函数，这就是函数思想的体现.

你有这个意识吗？

是不是想到使用函数的性质？

一旦你把表达式看作函数，就要习惯用函数的性质去解决问题.

看栗子.

请独立思考3分钟.

解题过程中用到了指数函数的单调性.

你有这样的意识吗？

是不是能够根据需要主动构造函数？

这是更高层次的要求，也是观察学习者是否真正具备函数思想的重要途径.

构造函数解题的特征是：原来的题目中没有给出明确的函数，甚至不是一个函数问题，但是可以根据要解决的问题的特征及求解的目标，构造一个需要的函数，然后通过研究所构造的函数的性质，从而解决问题.

一言以蔽之，为有利于解题，我们要能够无中生有地创造一个函数出来.

看栗子.

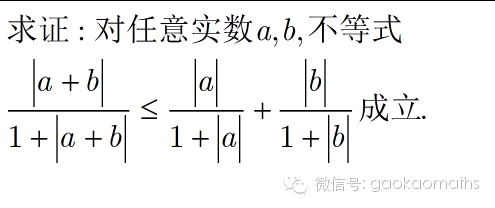
请独立思考3分钟.

分析：这个不等式的每一项的形式都相同，这就促使我们用一个共同的式子来统一，即构造一个函数.

事实上，上面用到的函数也称为“糖水函数”.把1看作水的质量，x看作糖的质量，则f(x)表示糖水的浓度.

显然，随着糖----溶质x的增加，糖水变得更甜一些，即糖水的浓度增大，说明f(x)是x的增函数.

你也练练手

看栗子.

分析：等式左边的两个括号内的代数式形式是一样的，这促使我们想到构造函数.

同时，为有利于分离这两个括号，我们构造一个含有对数符号的函数.

今天的栗子真多，而且还很甜.

从上面的栗子得到这样的经验：遇到形式相同的代数式时，我们往往联想到构造函数.

回到最初

该收尾了，回到最初童鞋提出的这道浙江高考题上.

选项中等式两边是不是形式很接近？

肿么办？

构造函数呗.

有童鞋问，为什么不构造函数f(x)=e^x-2x呢？

为神马呢？

哎，这个函数单调性不好确定啊.

本文你一定要再读一遍，看看这三行红字是否已经融入你的血液.