2016 年 7 月 30 日至 8 月 7 日,第 39 届欧洲杂耍大会(European Juggling Convention)在荷兰的阿尔梅勒举行, 8 月 3 日凌晨的搏击之夜(Fight Night)自然再度成为了众人关注的焦点——它是杂耍斗(combat juggling)这项运动最大的赛事。在杂耍斗的圈子里,有两个响当当的大名你必须要知道:德国选手 Jochen Pfeiffer 目前世界排名第二,之前拿过 6 次搏击之夜的冠军;英国选手 Luke Burrage 目前世界排名第一,之前拿过 8 次搏击之夜的冠军。这一年的比赛中,两位老将均以完胜的成绩轻松进入 32 强,并在淘汰赛阶段过关斩将,最终成功在决赛场上相遇。最终,世界排名第二的 Jochen 以 5 比 4 的成绩击败了世界排名第一的 Luke ,夺得了又一个搏击之夜的冠军。
杂耍斗是一种两人对战类的体育运动。比赛规则非常简单。每局比赛开始时,两名选手各自抛耍 3 个杂耍棒。任何一方都可以故意上前干扰另一方(但只能针对对方手中的或者空中的杂耍棒,不能针对对方的手臂和身体)。谁站到最后,谁就赢得该局。先赢 5 局者获得比赛的胜利。
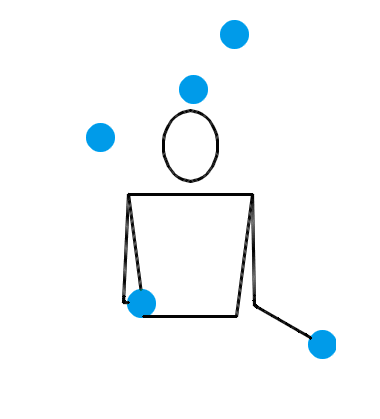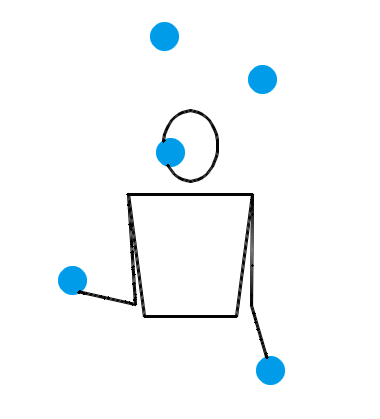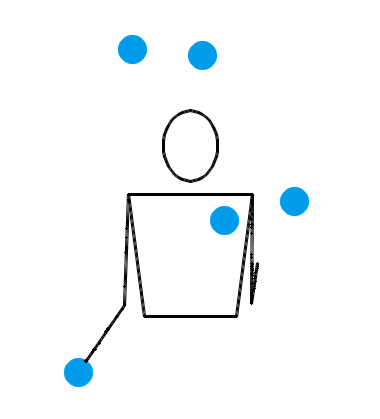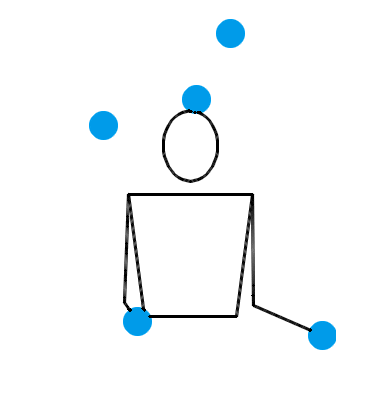
典型的一局比赛大致就像下面这样。这是 Jochen 和 Luke 的第 6 局比赛。
这场决赛确实打得精彩,出现了很多漂亮的瞬间。比如,在第 5 局比赛中, Jochen 做出了一个非常漂亮的防守动作。注意他在最后是如何改变自己的抛耍模式,在不违规的情况下(控制至少 3 个杂耍棒且任意时刻至少有一个杂耍棒在空中)抵挡住对手进攻的。
第 7 局比赛出现了更有意思的局面: Luke 从对方手中抢来了一个杂耍棒,于是在对方满地捡棒子时,自己居然抛耍起了 4 个杂耍棒!
不知道有没有人仔细看过视频后,发现了一个有趣的细节: Luke 虽然抛耍起了 4 个杂耍棒,但是他的动作好赖皮呀!用哪只手抛出的杂耍棒,就用哪只手接住,任何一个杂耍棒都没有在两手之间交替。这恐怕不能叫做杂耍吧!这是不是要算违规呀?
还真不是。两只手各自独立地抛耍 2 个物体,确实是一种基本的杂耍模式。让我们来看三个演示动画,它们分别对应抛耍 3 个物体、抛耍 4 个物体和抛耍 5 个物体时最基本的杂耍模式:
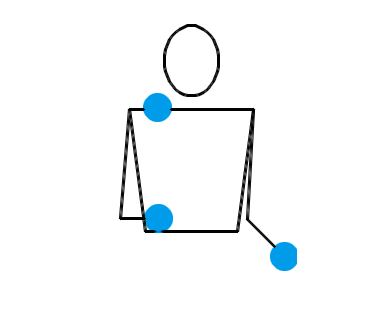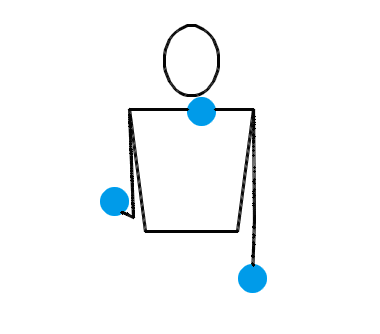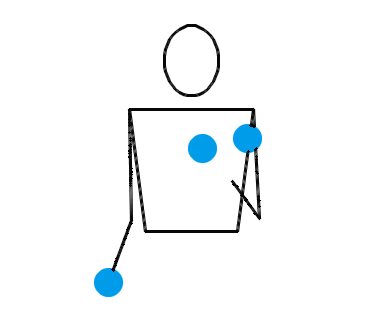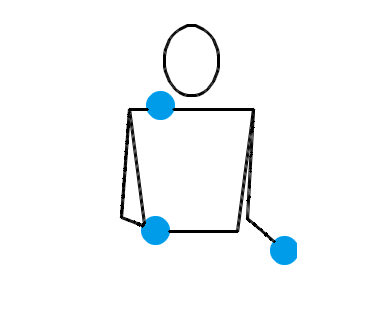
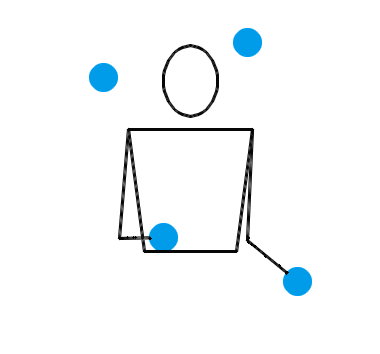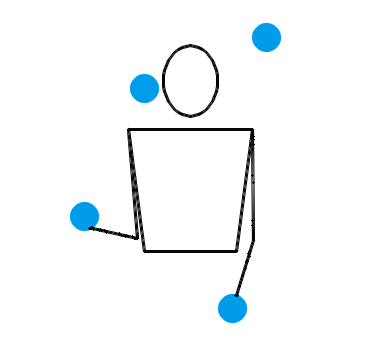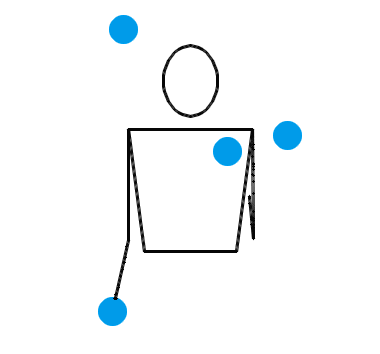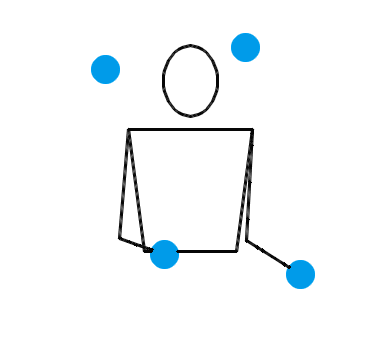
按照大多数人的理解,在任何一种杂耍模式中,左右两只手一定是交替地、有节拍地不断抛耍小球。也就是说,右手接住某个小球并立即把它重新抛出,片刻后就该轮到左手接住某个小球并把它抛出,再过相同的时间后就又该轮到右手接住某个小球并把它抛出……今后,我们把某只手接住并抛出某个小球叫做一次“接抛”。接抛动作将会以右手、左手、右手、左手的顺序轮流完成。我们假设每次接抛动作都是瞬间完成的,小球停留在手中的时间忽略不计。接下来,我们还会把相邻两次接抛之间的时间叫做“一拍”。我们假设杂耍过程中,每一拍的时长都是相同的。
上面这些杂耍模式之所以是“最基本的杂耍模式”,其实就是因为,每次接抛动作都是完全相同的。这意味着,每个小球每次都被抛到了相同的高度,都会在空中停留相同的拍数。如果每个小球都在空中停留 3 拍,结果会怎样呢?让我们画个图来分析一下:

图中,横坐标表示时间,纵坐标表示高度,弧线则表示随着时间的流逝,小球们的高度是如何变化的。每个小球都在空中停留了 3 拍,表现在图上就是,每条弧线都横跨了 3 个区间。由图可知,这里面实际上一共有 3 个小球(我们用 3 种不同的线条分别表示出了它们的轨迹)。此时,每个小球都会交替地来到左手和右手上。
类似地,如果每个小球都在空中停留 5 拍,我们就需要 5 个小球,才能让双手不会闲下来。可以看到,在这种情况下,每个小球也都会交替地来到左手和右手上。
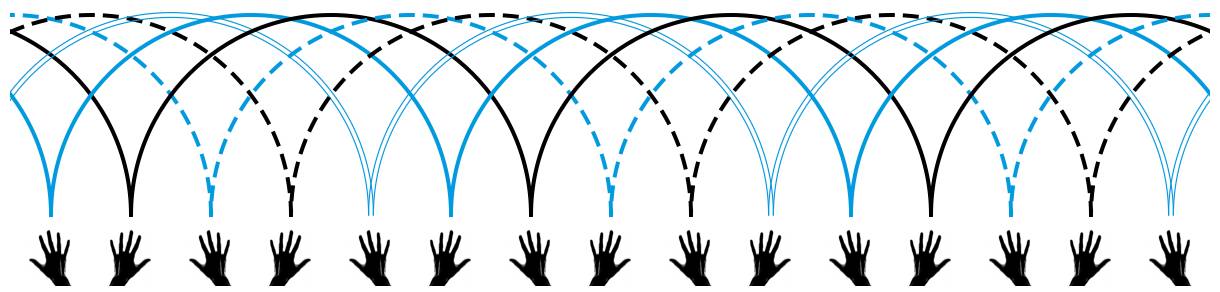
然而,如果每个小球都在空中停留 4 拍,情况就不一样了:对于任意一个固定的小球来说,不管它被哪只手扔了出去, 4 拍之后它将回到同一只手中。可以看到,此时对应着小球数为 4 的情况,也就是上面三个动画中的中间那个动画。
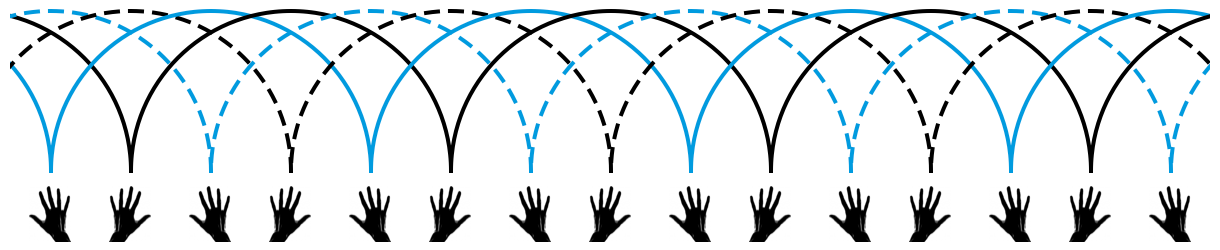
不妨用 n 来表示杂耍模式中的小球数。正因为在这种最基本的杂耍模式中, n 的奇偶性会导致如此大的区别,所以当 n 为奇数和 n 为偶数时,这种杂耍模式的俗名都是不一样的。当 n 为奇数时,所得的杂耍模式叫做“瀑泻”(cascade);当 n 为偶数时,所得的杂耍模式叫做“喷泉”(fountain)。
难道当 n = 4 时,就没有什么左右手能互相传递小球的杂耍模式吗?倒也有,比方说用一种叫做“倾盆”(shower)的杂耍模式就行了。事实上,倾盆可以适用于一切的 n ,并且不管 n 是奇数还是偶数,每个小球的位置都会在左右手之间切换。不过,这种模式的问题是——它太水了,还是不像杂耍。让我们还是先来看看 n = 3, 4, 5 时倾盆的演示动画吧:
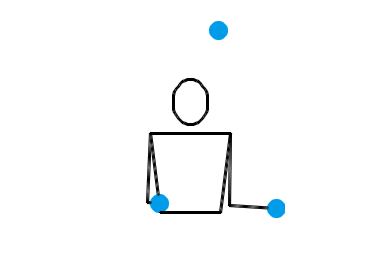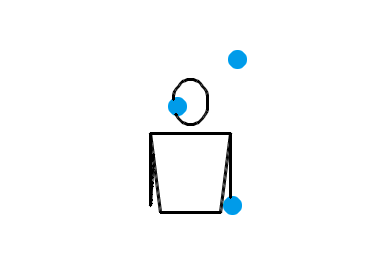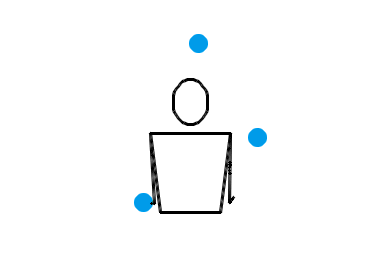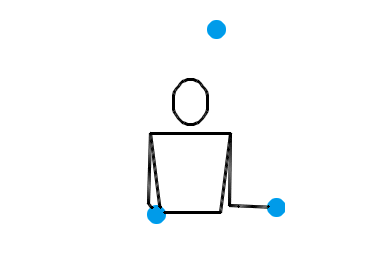
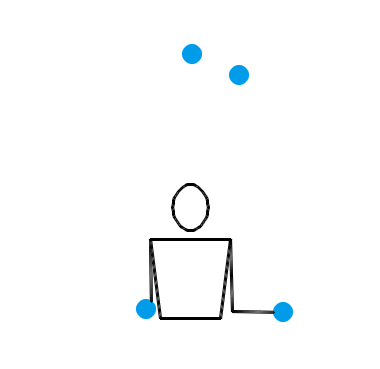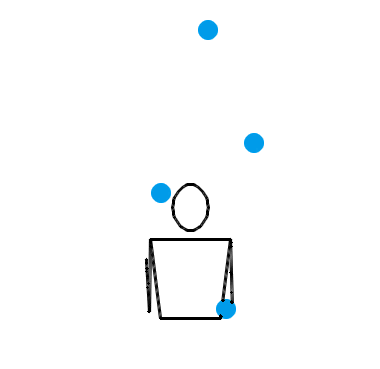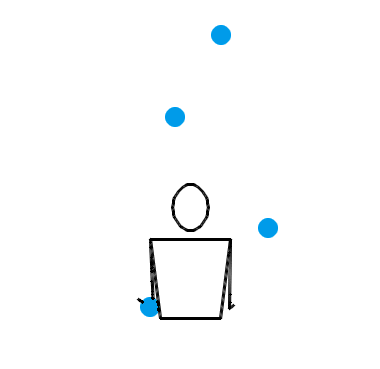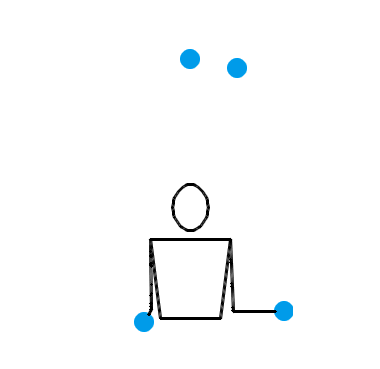
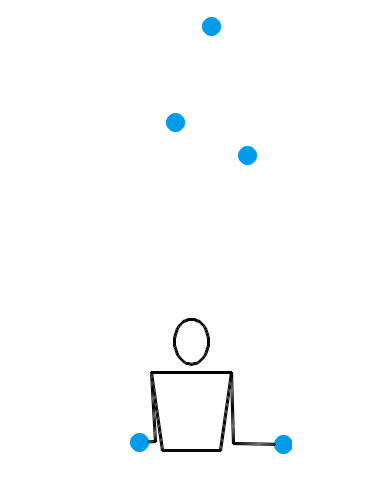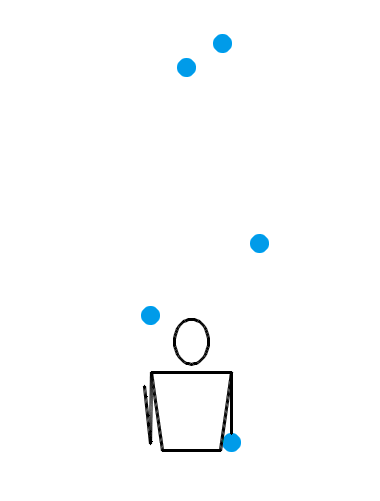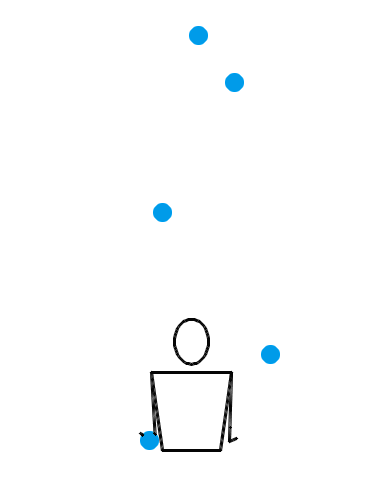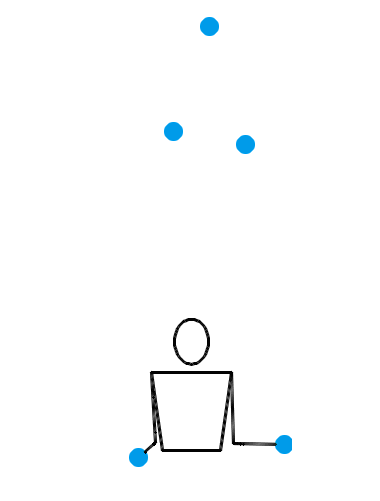
也就是说,左手接住并水平抛出某个小球,右手立即接到该球并把它抛到更高的地方;然后左手接住并水平抛出下一个小球,右手立即接到该球并把它抛到更高的地方……倾盆也算是非常基本的一种杂耍模式了,或许你自己没事儿时也偷偷尝试过。搜索与“杂耍”有关的插图插画,画面内容基本上都是一个人把一堆小球从一只手扔到另一只手,所有小球在空中大致排成一个半圆。这表现的其实就是倾盆这种杂耍模式。不过,和瀑泻比起来,倾盆的效果确实差了一些,少了点“左右开弓”的感觉。
说了半天,当 n = 4 时,究竟有没有什么看起来非常爽,观赏性非常强的玩法呢?有。来看看下面三种 n = 4 时的杂耍模式:
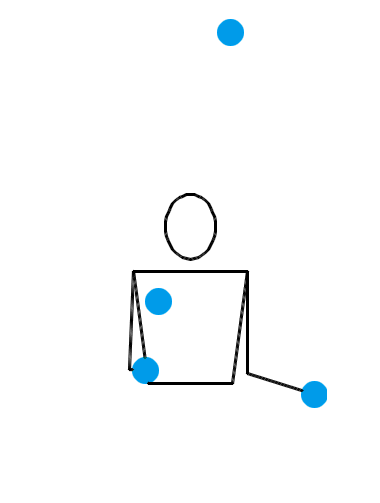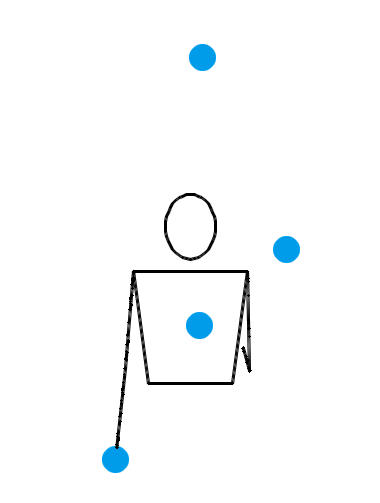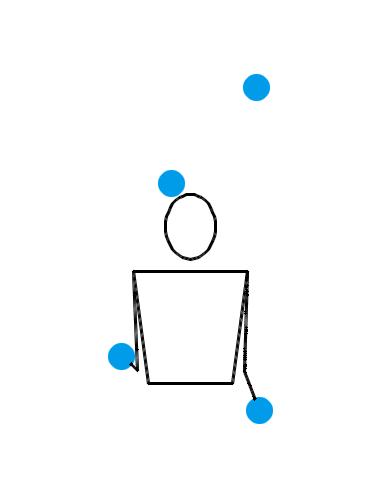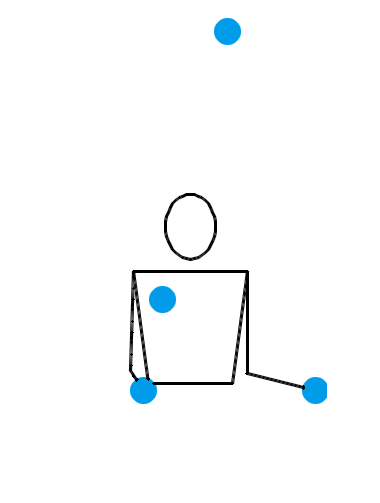
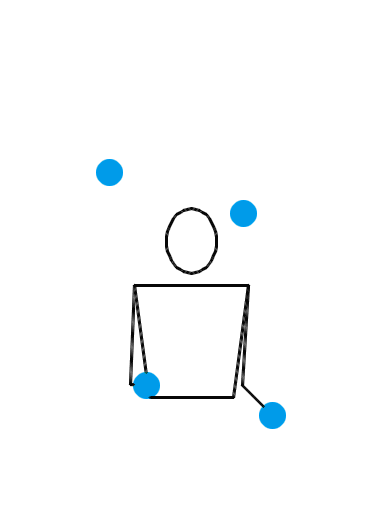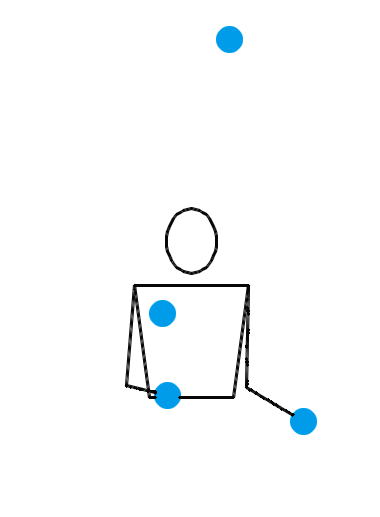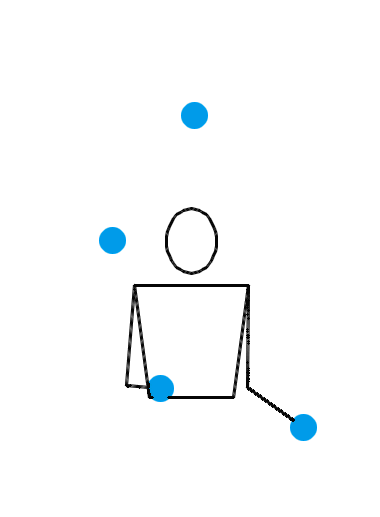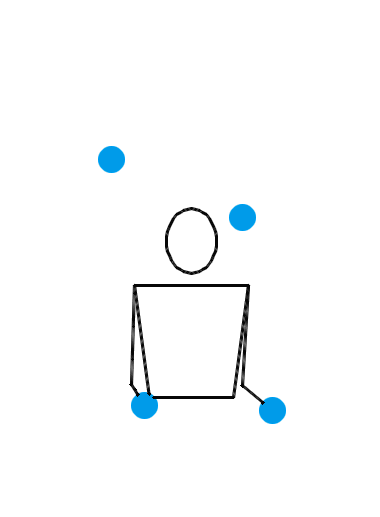
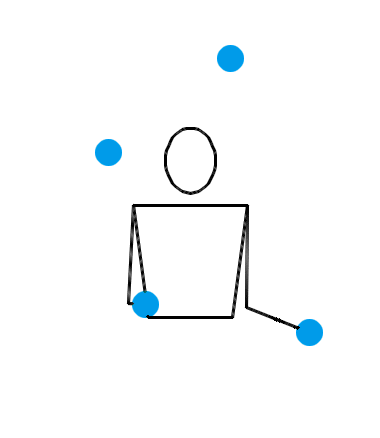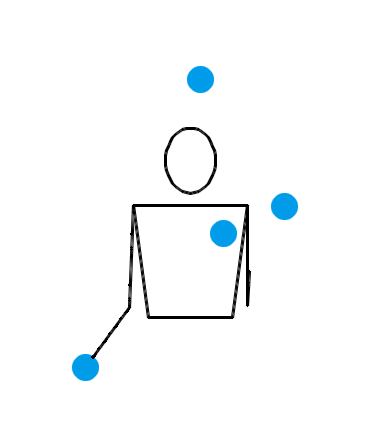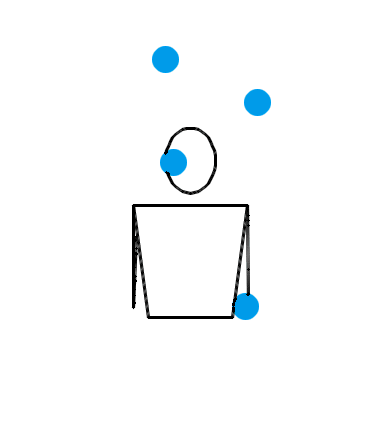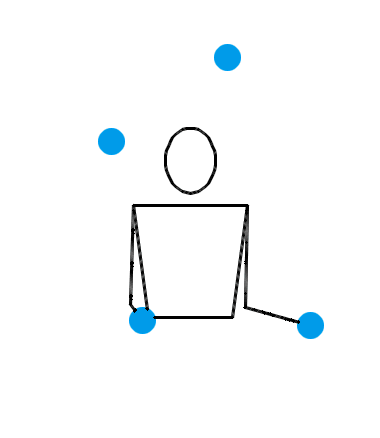
看了上面这三个动画,你有何感想?我估计,你的第一反应会是:“真牛逼,没想到这背后的水这么深!看着就觉得里面有好多数学原理!”接下来,你就该观察各种细节,或者该冒出各种怪异的想法了:
“我操,这些动画你丫都是拿什么软件做的呀?”
“你这网站上写的东西今后肯定是要出书的吧?哼哼,我看到时候这篇文章的动画你怎么处理!”
“你说这些新的杂耍模式都是谁想出来的,都是怎么想出来的呀?”
“这三种杂耍模式真的是三种不同的杂耍模式吗?让我看看啊……哦,是,好像确实是不同的。”
“这三种杂耍模式的循环长度似乎是不一样的,最左边那个的循环长度明显要短得多。”
“其实中间那个杂耍模式中,右手还是出现了自己扔给自己的情况。哦,左手也出现了这种情况。咦,等等,好像这个杂耍模式中,左右手的动作是完全对称的!”
“最右边那个图我好像看出些名堂来了。它就是一个抛得更高的 3 球瀑泻,插进去一个简单的水平抛掷。”
……
好吧,我先专门说一下这些动画是怎么变出来的吧,不然大家肯定又会问。以前每篇文章的图片和动画都是我用 Mathematica 做的,但这篇文章还真不是。这篇文章中所有杂耍模式的演示动画都是用一个叫做 Juggling Lab 的开源软件生成的(然后用 ImageMagick 调了一下颜色和线条的粗细)。这个软件在杂耍界里非常有名,它可以生成各种杂耍模式的 GIF 演示动画,极大地方便了人们的交流。
这篇文章里有这么多动画,以后真的出书时该怎么办呢?那还有啥办法,到时候出书时只能不用这篇文章了呗!所以,大家一定要体会到科技的进步。现在,向其他人展示某种杂耍模式,只需要发个 GIF 动画就行了;但在只有纸媒的时代,这将会变得非常非常困难。《杂耍者世界》(Juggler’s World)是杂耍界里颇有影响力的杂志。杂志读者曾经问道:为什么不在杂志上教大家一些新的杂耍技巧呢?于是,在 1985 年第 2 期的杂志中,编辑们用一组照片辅以数字和箭头,详细讲解了一个抛耍 4 球的新玩法。自然,效果非常糟糕,至少我看了半天都没看懂。

就好像跳水中“5253B”表示“向后翻腾两周半转体一周半屈体”一样,要是我们有一套记号,或者说一种“语法”,可以简单有效地表示出各种杂耍模式就好了。人们不但可以借助它进行交流,或许还能通过摆弄这些符号,寻找新的杂耍模式。杂耍模式的很多特征,或许也会反映在这些符号当中。
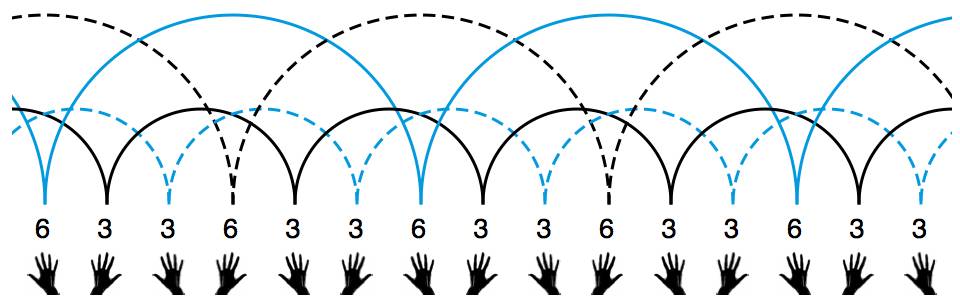
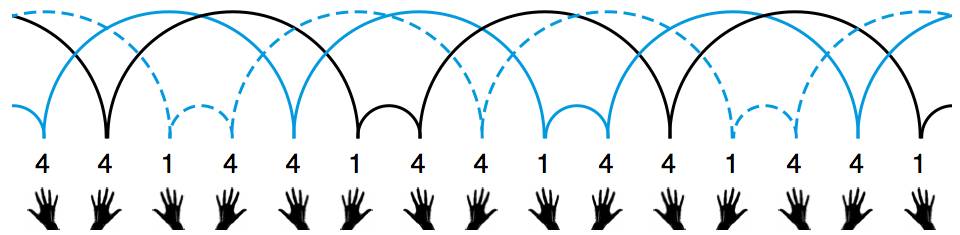
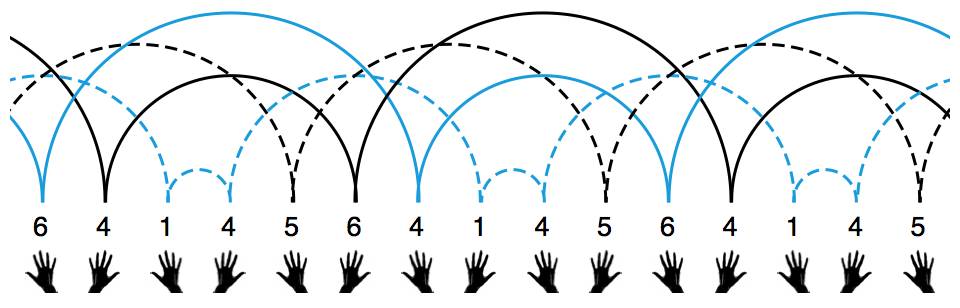
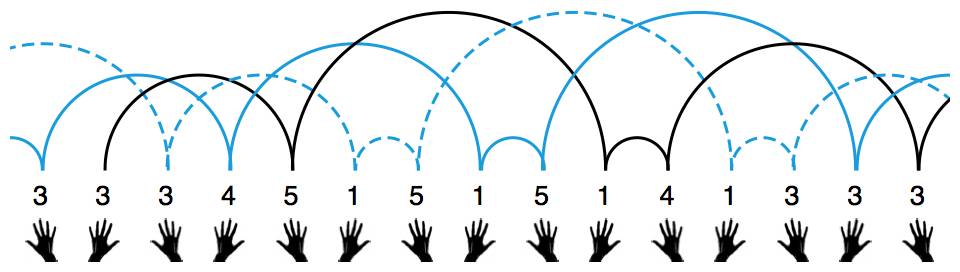
刚才对瀑泻和喷泉的分析,让我们自然地想到了这样一种方案:依次记下每次扔出的球会在空中停留几拍,直到完整地记下一个循环节为止。刚才我们展示了三种非常高级的 4 球玩法,让我们仔细分析一下中间那种玩法。不妨从右手扔出最高的那一次球开始算起:这次扔出的球(由右手扔出)要过 5 下才会被接住,我们就用数字 5 来标记;下次扔出的球(由左手扔出)要过 3 下才会被接住,我们就用数字 3 来标记;第三次扔出的球(由右手扔出)要过 4 下才会被接住,我们就用数字 4 来标记……如果把小球的轨迹连同这些数字标记一并画出,大概就是这样:
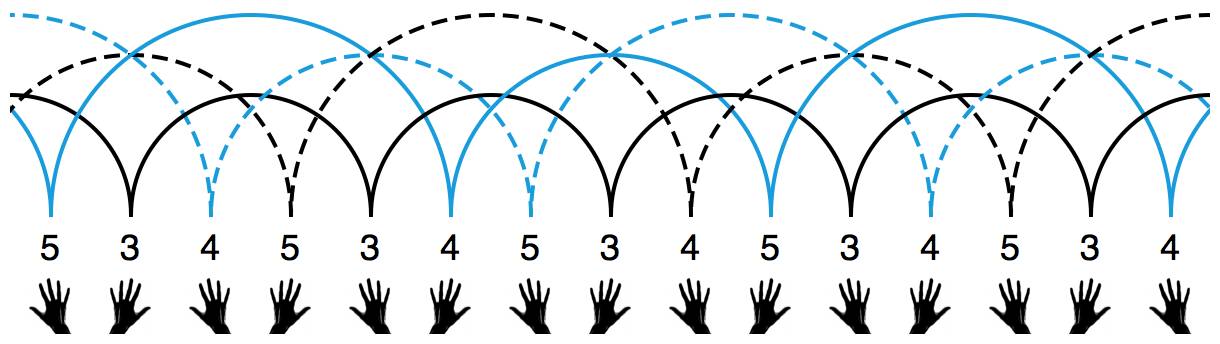
杂耍模式能永远持续下去,肯定是因为它在不停地循环。在这个例子中,我们记下的数字形成了 534 循环。我们就用 534 来表示这种杂耍模式。这就是杂耍界最通用的杂耍模式记号——“位换记号”(siteswap)。
位换记号最早是由谁想出来的,现在已经很难考证了。目前一般认为,位换记号起源于 1985 年左右,它的发明和传播,至少与以下三组人马有着密切的关系:来自加利福尼亚州圣克鲁斯的 Paul Klimek ,来自加利福尼亚理工学院的 Bruce Tiemann 和 Bengt Magnusson ,以及来自英国剑桥的 Michael Day 、Colin Wright 和 Adam Chalcraft 。
对于杂耍表演者来说,位换记号是非常直观的,因为它记录的本质上就是杂耍时的一个个接抛动作:数字 1 就表示,我应该把刚接到的球近乎水平地扔向另一只手,让另一只手在下一拍立即接到它;数字 2 就表示,我应该把刚接到的球竖直向上扔一点,使得在另一只手完成动作后,正好轮到这只手重新把它接住(实际表演时,人们通常会选择直接把这个小球握在手中停留 2 拍,因为在此期间反正这只手也不需要干别的);数字 3 就表示,我应该把刚接到的球扔得更高一些,扔出一个抛物线,使得 3 拍之后另一只手正好能接住它……总之,数字越大,就意味着我应该把小球越得越高,并且偶数意味着应该竖直向上扔,奇数意味着应该往另一只手的方向扔。
事实上,位换记号只告诉了你扔出的球需要多久之后回到手中,而并没有告诉你这个球具体应该怎么扔出去。你可以从胯下扔上来,从身体背后扔过来,扔头上顶一会儿,扔地上反弹回来……只要它能在正确的时候被接住就行了。
注意,一个杂耍模式的位换记号往往不是唯一的。我们可以对位换记号中的数字进行“循环移位”(cyclic shift),例如把 534 变为 345 和 453 ,它们刻画的显然是同一个杂耍模式。此时,人们通常会选择使用字典序最大的那个记法(也就是说,使用第一位数字最大的记法,如果有多个第一位数字最大的,则使用它们之中第二位数字最大的记法,等等)。另外,人们通常假设,位换记号中不会有大于 9 的数字出现,因为把小球扔这么高是不太现实的。这样的话,每个杂耍模式的位换记号都是一串唯一确定并且没有歧义的数字了。
我们刚才介绍的那些杂耍模式,用位换记号都该怎么记呢? 3 球瀑泻、 4 球喷泉、 5 球瀑泻的位换记号分别是 3 、 4 、 5 。果然,它们是最基本的杂耍模式。 3 球倾盆、 4 球倾盆、 5 球倾盆的位换记号分别是 51 、 71 、 91 。这也很容易看出来。
最后我们展示了三种 4 球玩法,其位换记号从左至右依次为 53 、 534 、 5551 。之前观察到的现象和规律,都可以从这几个位换记号中读出来。左边那个的循环长度确实是最短的,因为它的位换记号的长度就是最短的。整个杂耍模式其实就是两个动作不断重复,右手做个 5 ,左手做个 3 ,右手再做个 5 ,左手再做个 3 。中间那个的位换记号里有偶数,因此它里面就会出现“自己扔给自己”的情况。同时,它的动作是左右对称的,因为它的位换记号的长度为奇数。第一轮的 534 分别对应右、左、右,第二轮的 534 就分别对应左、右、左了。右边那个本质上就是“一个抛得更高的 3 球瀑泻,插进去一个简单的水平抛掷”,它的动作要领显然就是三个相同的大动作加上一个小动作,这不正是 5551 的意思吗?
不知道大家有没有发现, 53 、 534 、 5551 这几串数字有一个共同特征:数字串里所有数字的平均数都是 4 。事实上,这个规律对于其他几个杂耍模式的位换记号也都成立:位换记号中所有数字的平均数,等于这个杂耍模式中小球的个数。这就是位换记号理论中最著名的一个定理——平均数定理(the average theorem)。这个定理为什么是对的呢?我们介绍一种非常直观的证明方法。
每个小球每次在空中停留的时间,完全是我的手在抛出它时给予它的。这就好比每次抛出小球都是在给小球加油一样。如果位换记号里有一个数字 4,就表示此时抛出小球的动作相当于给小球加了 4 个单位的油,小球也就会在空中停留 4 个单位的时间,直到最后没油了落回手中,继续接受下一次加油。每个循环刚开始的时候,有些空中的小球消耗的还是上一个循环里加的油;每个循环快结束时,给小球加的油也有一部分会放到下个循环去用。但是,既然这些循环能够一个接一个地无限持续下去,既不会出现剩余的油越积越多的情况,也不会出现油慢慢就不够了的情况,这就说明每个循环里给小球加的油,一定都恰好等于这个循环里所有小球在空中停留的时间之和。
假设某个杂耍模式有 n 个小球,其位换记号的长度为 l 。在每个循环里,我的手一共给小球加了多少油呢?显然,这等于位换记号里的所有数字之和。在每个循环里,所有小球在空中总共停留了多少时间呢?由于我们有 n 个小球,每个小球都在空中停留了 l 个单位的时间,所以答案就是 n · l 。于是我们得到,位换记号里的所有数字之和等于 n · l ,即 n 等于位换记号里的所有数字之和除以 l 。这正是平均数定理的内容。
平均数定理有一个重要的推论:瞎写一串数字,不见得是一个合法的位换记号。比方说,如果所有数字的平均数根本就不是整数,那么这串数字就必然不是一个合法的位换记号了。然而,麻烦的是,即使所有数字的平均数是个整数,这串数字也不见得是一个合法的位换记号。比方说, 6114 这串数字满足平均数条件,但它就不是一个合法的位换记号。在 61146114… 中,第一次抛出的小球和第六次抛出的小球会“撞车”,使得杂耍模式无法持续下去。
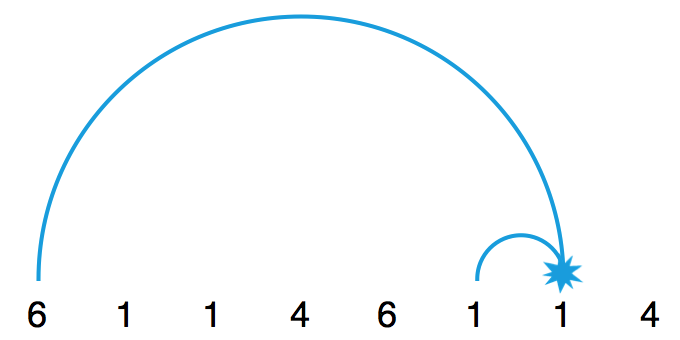
所以,位换记号可以很好地描述杂耍模式,但要想利用位换记号创造新的杂耍模式,还得想想办法才行。
不妨让我们换个思路:能否对已有的位换记号进行改造,从而得出新的杂耍模式呢?考虑之前提过的 534 模式。现在,如果把 534 改成 633 ,会出现什么有意思的结果?你会发现,整个杂耍模式的循环节长度仍然是 3 ,并且在每一个循环节中,第一次抛出的小球和第三次抛出的小球都会交换落点。所以,原来的位换记号不会出现撞车的情况,新的位换记号也不会出现撞车的情况。
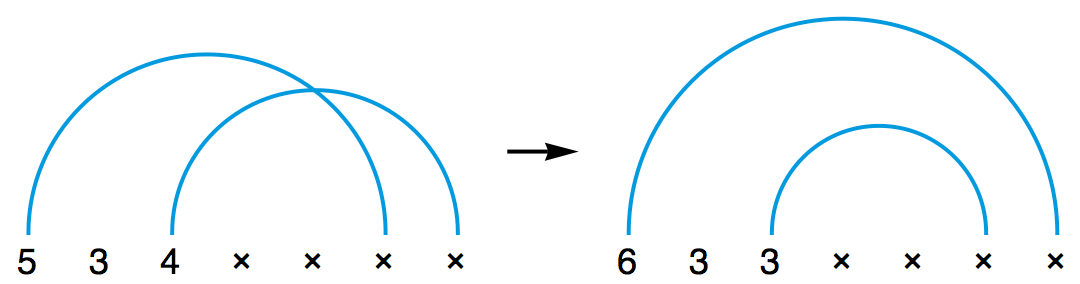
我们预言: 633 是一种新的合法的位换记号,对应于一种全新的杂耍模式!事实上确实如此:
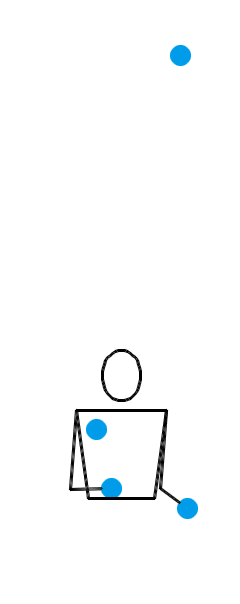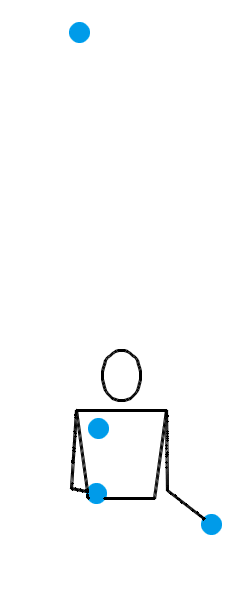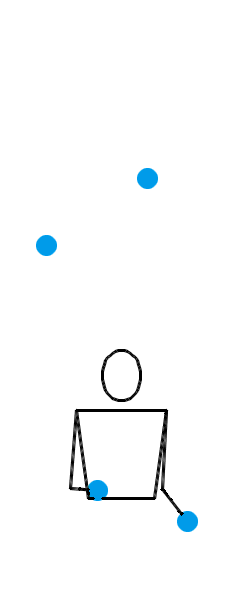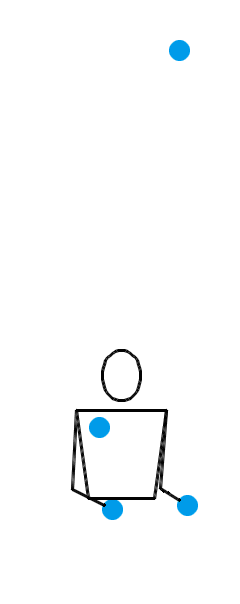
一般地,如果位换记号中有 a 、 b 两个数字,它们相隔 d 拍的距离,那么把 a 和 b 分别换成什么数字,就能交换它们的落点呢?看看下图,你就知道了:我们应该把 a 换成 b + d ,把 b 换成 a – d 。
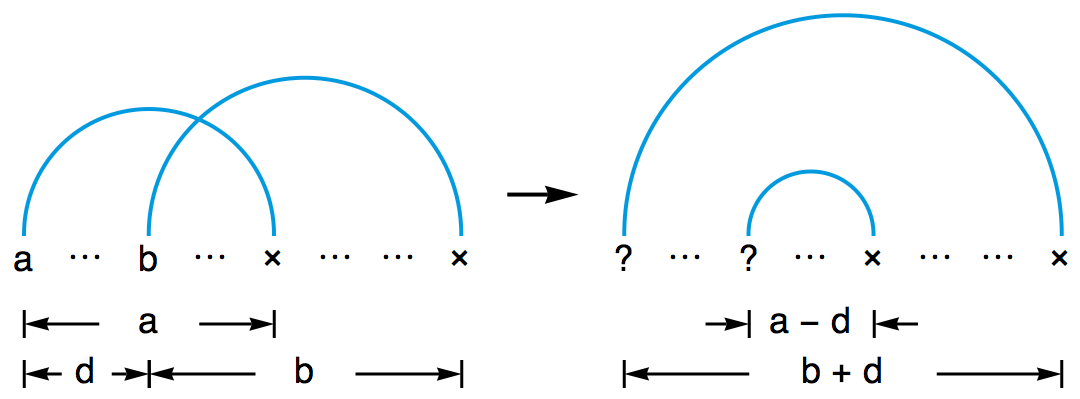
在数字串中,按此规律修改某两个数字的操作就叫做一次“位换”(site swap)。对合法的位换记号进行位换操作,得到的仍然是合法的位换记号。其实,“位换记号”这个词就是这么来的——它是一种支持位换操作的记号。注意,每次位换既不会改变位换记号的长度,也不会改变位换记号中的所有数字之和。因此,位换操作不会改变所有数字的平均数。这说明,用位换操作得到的新杂耍模式,与原杂耍模式的小球数是相同的。
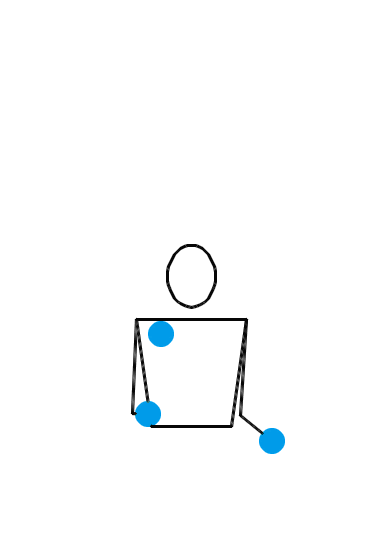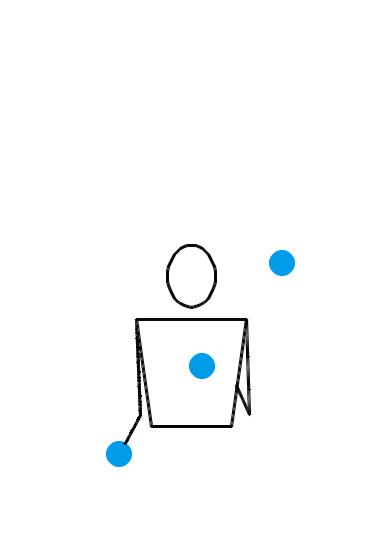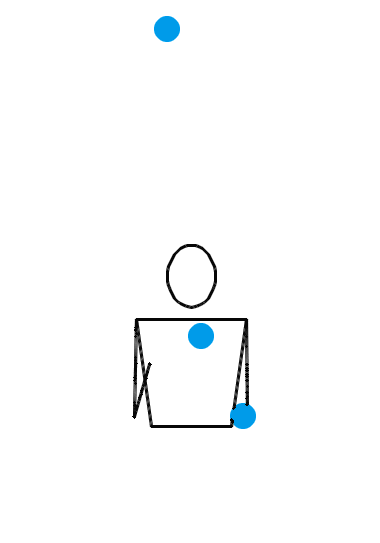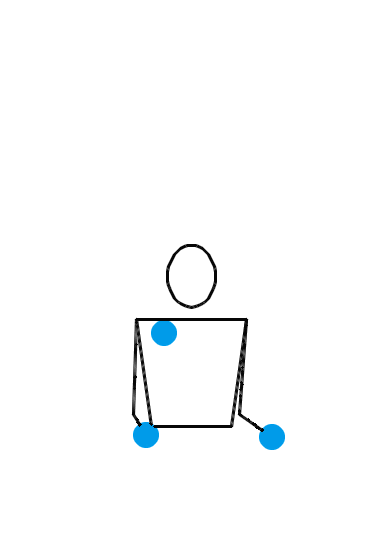
位换操作很强大。让我们再给大家展示几个例子。如果你愿意,你甚至可以对 3 球瀑泻进行位换操作。 3 球瀑泻的位换记号是 3 ,里面就只有一个数字,这可怎么做位换呢?没关系,多补几个循环节就行了。比方说,把 3 先扩写成 333 ,然后对第一个数字和第三个数字进行位换,于是得到 531 。那么, 531 就是一个新的杂耍模式。如果我们刚才选择把 3 扩写成 3333 ,但还是对第一个和第三个数字进行位换,得到的当然就是 5313 。类似地,把 3 扩写成 33333 ,位换后还能变出 53133 来……于是,我们知道了, 531, 5313, 53133, 531333, … 都是合法的位换记号。下面三个动画展示的分别是 531 、 5313 和 53133 的玩法。
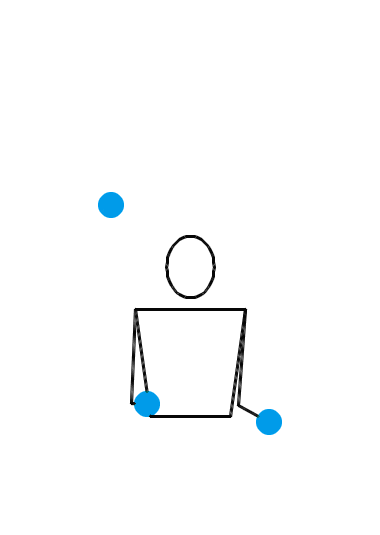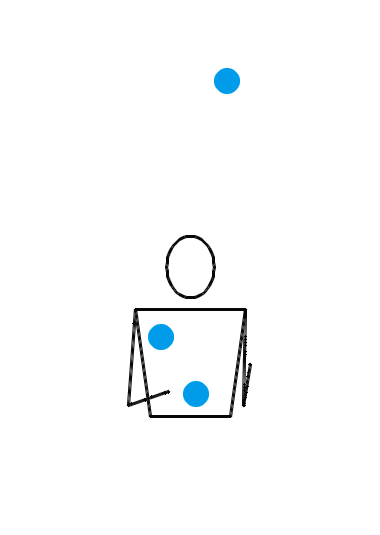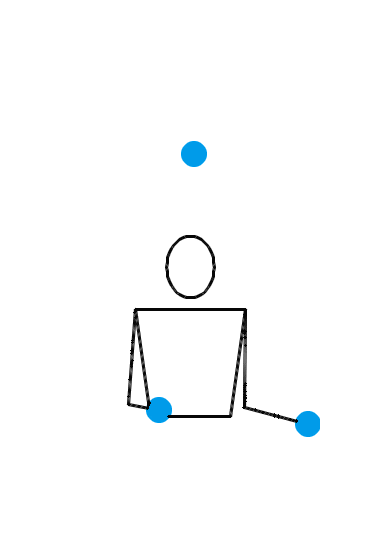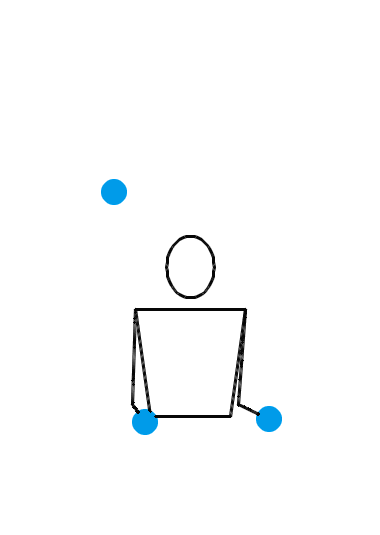
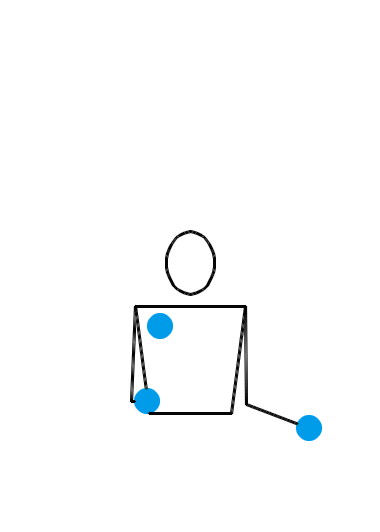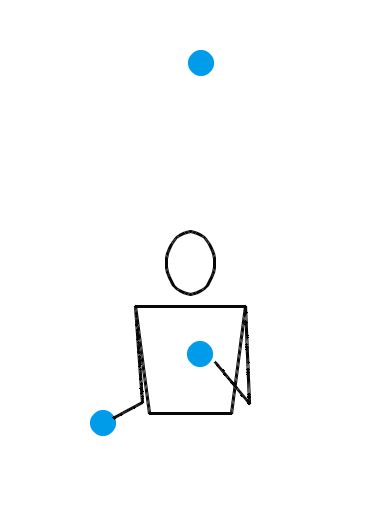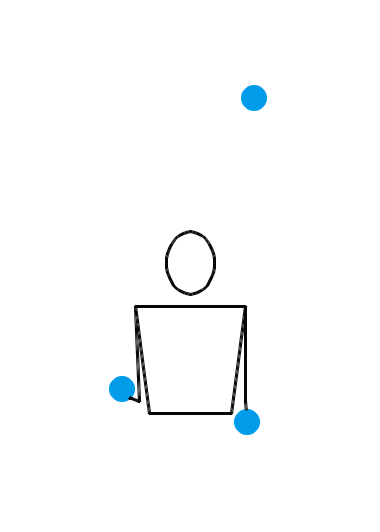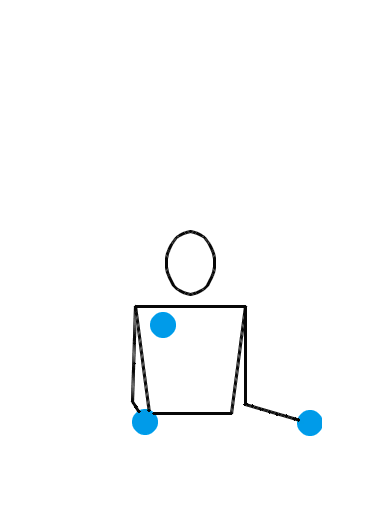
我们还可以对位换之后的结果再做位换。比方说,对 531 的第一个和第二个数字进行位换,于是得到 441 。这就又是一种新的杂耍模式!
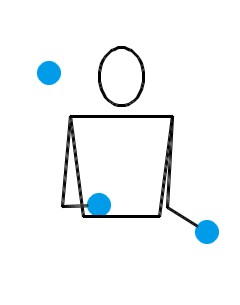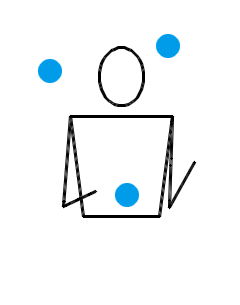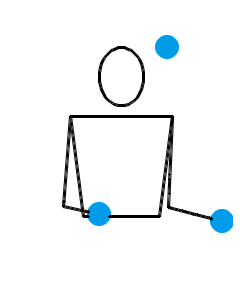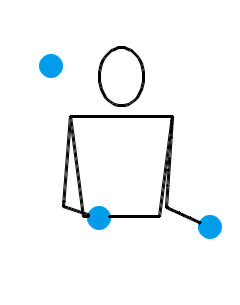
441 模式可以说是人们利用位换记号得到的最大的成果之一。以前,人们凭借想象,发明创造了各种各样的杂耍模式,并给它们起了各种各样的名字。但在位换记号提出之前,由于缺乏系统的研究工具,很多简单的玩法都没被发现。在位换记号理论的帮助下,人们找到了很多新的杂耍模式, 441 模式就是最经典的例子之一。也正因为这样, 441 模式就不再有什么别的名字了。杂耍界的人们直接管它叫 441 。
我们刚才是用 3 → 333 → 531 → 441 的办法生成的 441 。其实,生成 441 还有很多别的路子。比方说,还是先把 3 扩写成 333 ;接下来,对 333 的第一位和第二位进行位换,于是得到 423 ;循环移位,可以把 423 变成 342 ;再对 342 的第一位和第三位进行位换,就可以得到 441 了。当然,变出 441 并不需要那么复杂,其实 423 能直接变成 441 。这里我们只是想告诉大家,位换操作还可以和循环移位配合着使用。
1993 年, Allen Knutson 证明了一个非常漂亮的结论:先对某个单数字的位换记号进行扩写,再通过适当的循环移位和位换操作,就能变出一切合法的位换记号!由于循环移位和位换操作都不会改变位换记号的长度和平均数,因此为了得到位换记号长度为 l 的 n 球玩法,我们必须先把单个数字 n 扩写成 l 个数字 n 。所以,接下来我们只需要说明,任何一个位换记号长度为 l 的 n 球玩法,都能从 l 个数字 n 出发,通过循环移位和位换操作得出。
考虑这样一个位换记号处理算法:
如果数字串里的所有数字都相同,则输出该数字串,算法结束
使用循环移位操作,将最大数字挪至第一位,同时使得第二位数字和第一位数字不同
对第一位数字和第二位数字进行位换操作,然后跳转到第 1 步
把任意一个合法的、长度为 l 的、平均数为 n 的位换记号输入该算法,都会经过一系列的循环移位和位换操作,最终变成 l 个数字 n 。注意到,如果数字串 A 循环移位后能变成数字串 B ,数字串 B 显然也能通过循环移位变成数字串 A 。另外,容易验证,如果对数字串 A 做一次位换后得到数字串 B ,则在同样的位置上对数字串 B 做一次位换,又会变回成数字串 A 。既然每个合法的位换记号都能变成 l 个数字 n ,那么从 l 个数字 n 出发,也就能反过来变出每个合法的位换记号了。
等等,这也太简单了吧,好像我们漏掉了什么吧?嗯,是的。我们还得证明:把任意一个合法的位换记号输入该算法,该算法在有限步之后一定会终止。
首先注意到,由于合法的位换记号经过循环移位和位换操作后仍然是合法的,因此把任意一个合法的位换记号输入进去,算法生成的自始至终都是合法的位换记号。现在,假设在做第 3 步时,数字串的头两个数字是 a 和 b 。根据之前的算法步骤可知, a 是整个数字串中最大的数,并且 a 与 b 不相等。换句话说, a 比 b 至少大 1 。事实上, a 不可能比 b 刚好大 1 ,否则这两个地方扔出的小球会撞车,这就不是一个合法的位换记号了。因此, a 比 b 至少大 2 。第 3 步之后, a 将会变成 b + 1 , b 将会变成 a – 1 。这说明,每过一遍第 3 步,数字串中都会有某个最大数减小了 1 ,并且不会因此而引入新的最大数。如果输入的位换记号中所有数字的平均数是 n ,那么所有数字的平均数就一直是 n 。等最大数不断减小,一直减小到 n 了,那么所有的数字都是 n 了,算法也就终止了。到此为止,我们就完整地证明了 Allen Knutson 的结论。
这个结论有一个非常强大的推论:对于任意一个合法的、长度为 l 的位换记号,将它的各个数字分别与 1, 2, 3, …, l 对应相加,所得的 l 个结果除以 l 的余数一定是各不相同的。由于除以 l 的余数正好也就只有 0, 1, 2, …, l – 1 这 l 种可能,因此上述推论还可以重新叙述为:按上述步骤做加法并取余,所得的 l 个结果正好构成 0, 1, 2, …, l – 1 的一个排列。举个例子,在 441 模式中, 4, 4, 1 依次与 1, 2, 3 相加,得到的结果为 5, 6, 4 ,它们除以 3 的余数分别是 2, 0, 1 ,正好是 0, 1, 2 的一个排列。再举个例子,之前我们曾经提到过 53133 模式,其中 5, 3, 1, 3, 3 依次与 1, 2, 3, 4, 5 相加,得到 6, 5, 4, 7, 8 ,它们除以 5 的余数分别为 1, 0, 4, 2, 3 ,正好是 0, 1, 2, 3, 4 的一个排列。我们就说, 441 和 53133 都能通过“排列测试”(permutation test)。
为什么一切合法的位换记号都能通过排列测试呢?首先,如果位换记号中所有数字都相同,那它显然能通过排列测试。既然由此出发,通过循环移位和位换操作能得出其他一切合法的位换记号,因此我们只需要说明:能通过排列测试的数字串,经过循环移位和位换操作后,也照样能通过排列测试。事实正是如此。
首先说循环移位。将循环移位过的数字串与 1, 2, 3, …, l 对应相加,本质上就相当于是将数字串与循环移位过的 1, 2, 3, …, l 对应相加;而后者会使得所有的余数都循环移动一下,所以如果原来可以形成排列,那么现在依然可以形成排列。比方说,假设某个数字串原本是 a, b, c, d, e ;循环移位后,数字串变成了 c, d, e, a, b 。原来, a, b, c, d, e 应该与 1, 2, 3, 4, 5 对应相加;现在, a, b, c, d, e 就应该与 4, 5, 1, 2, 3 对应相加。把 a + 1 变成 a + 4 之后,除以 5 的余数会怎么变呢?不难看出,如果原来余数是 0 ,现在就会变成 3 ;如果原来余数是 1 ,现在就会变成 4 ; 2 则会变成 0 , 3 则会变成 1 , 4 则会变成 2 。换句话说,余数会按照 (0, 1, 2, 3, 4) → (3, 4, 0, 1, 2) 的规律发生变化。然而,把 b + 2 变成 b + 5 ,把 c + 3 变成 c + 1 ,把 d + 4 变成 d + 2 ,把 e + 5 变成 e + 3 ,除以 5 的余数都会按照这样的规律发生变化。所以,如果原来的 5 个余数既无重复又无遗漏地包含了 0, 1, 2, 3, 4 ,按照 (0, 1, 2, 3, 4) → (3, 4, 0, 1, 2) 的规律整体一变后,新的 5 个余数仍然既无重复又无遗漏地包含了 0, 1, 2, 3, 4 。
然后说位换。假设我们对相隔 d 拍的两个数字 a 、 b 进行位换。如果数字 a 本来应该与 i 相加,那么数字 b 本来就应该与 i + d 相加。相加之后的结果是 a + i 和 b + i + d 。位换后,数字 a 变成了 b + d ,数字 b 变成了 a – d 。前者还是要与 i 相加,后者还是要与 i + d 的相加。相加之后的结果就是 b + d + i 和 a – d + i + d = a + i 。看出来了吧!在位换前和位换后,相加之后的结果没变,只不过颠倒了而已。自然,除以 l 的余数也不会变,只是颠倒了而已。
所以,我们就证明了:一切合法的位换记号都能通过排列测试。反过来,无法通过排列测试的,必然就不是合法的位换记号了。排列测试比我们之前说过的平均数定理检验法更为强大。之前我们说过, 6114 不是一个合法的位换记号,但用平均数定理却无法检验出来。不过,如果换用排列测试来检验,就能立即见效了。 6, 1, 1, 4 分别加 1, 2, 3, 4 可得 7, 3, 4, 8 ,它们除以 4 的余数是 3, 3, 0, 0 。这说明, 6114 不能通过排列测试,它也就不是合法的位换记号了。
有没有什么数字串,它连排列测试都通得过,但仍然不是合法的位换记号呢?答案是否定的。我们可以证明,能通过排列测试的,也一定都是合法的位换记号。这背后的道理其实很简单。不妨让我们以 l = 4 为例。假设这个长度为 4 的数字串是 a, b, c, d 。如果把数字 a 所在的位置看作第 1 次接抛,那么 a + 1, b + 2, c + 3, d + 4 分别就是这 4 次接抛的落点位置。如果这个数字串能通过排列测试,就说明这 4 个落点正好是某个循环节中的第 1 个点,某个循环节中的第 2 个点,某个循环节中的第 3 个点,以及某个循环节中的第 4 个点(不管是什么顺序)。也就是说,这 4 个落点正好涵盖了循环节中的 4 个不同的地方。把这部分示意图平铺开来,你会发现,每个点都将会恰好有一接和一抛。这就是一个正确的杂耍模式了。
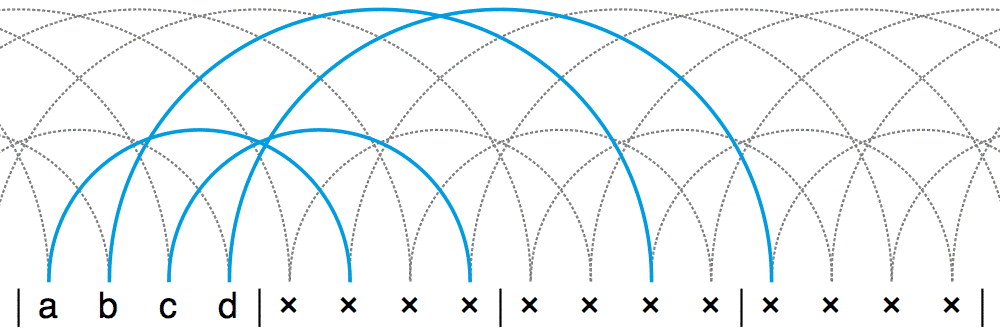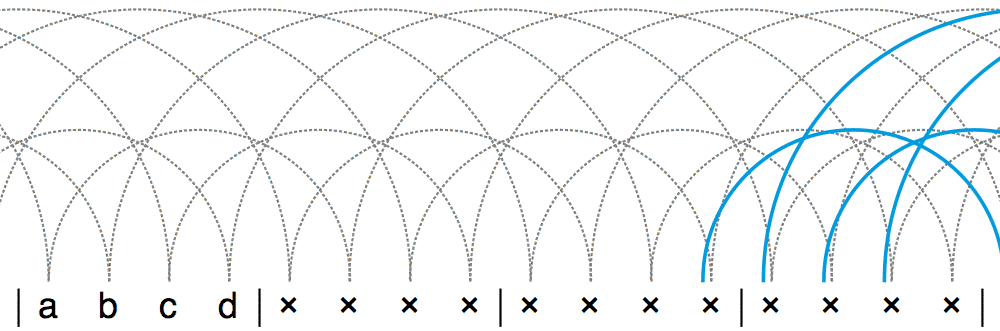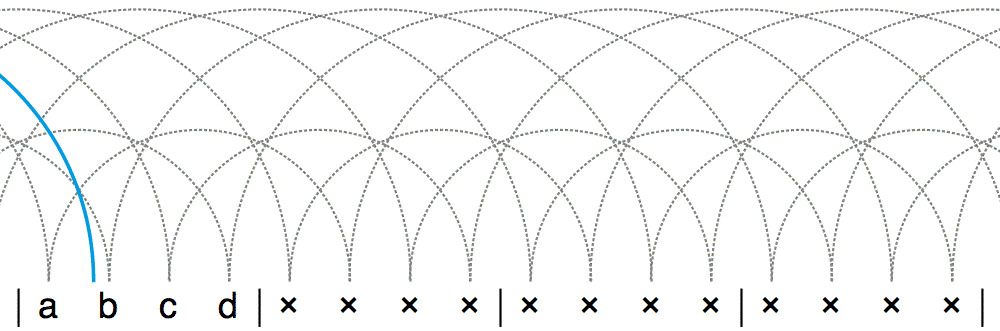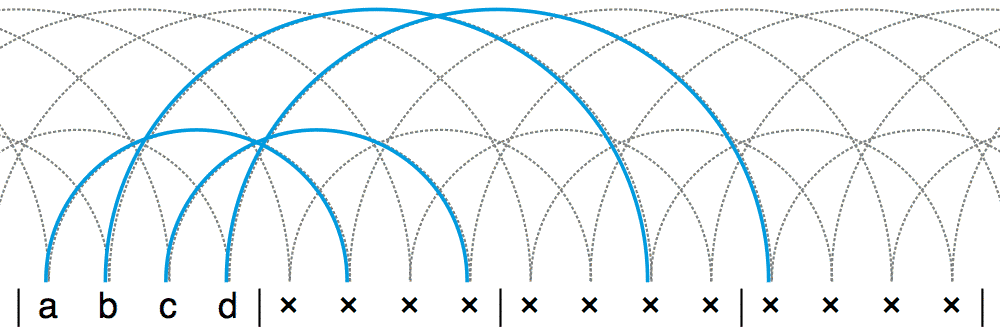
于是,我们证明了这样一个非常终极的结论:某个数字串是一个合法的位换记号,当且仅当它能通过排列测试!这又会产生很多有趣的推论。比方说,如果一个数字串能通过排列测试,那么让每个数字都增加或者减小一个相同的常数,得到的数字串显然仍能通过排列测试。因此,给一个位换记号中的每个数字都增加或者减小相同的量,就会得出新的杂耍模式。有的地方把这种改造位换记号的操作叫做“垂直移位”(vertical shift)。例如,对 441 进行垂直移位,可以依次得到 552 、 663 、 774 等,它们都是新的杂耍模式。下面三个动画分别是 552 、 663 和 774 的杂耍模式演示动画。左边那个动画是这篇文章中第一次出现的位换记号里含有数字 2 的情况。之前我们说过,在遇到数字 2 时,表演者通常会选择直接把这个小球握在手中停留 2 拍。另外,可以看到,和之前那些位换记号变换法不同的是,垂直移位可以改变杂耍模式中的小球数。
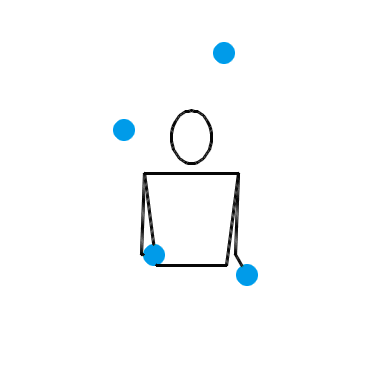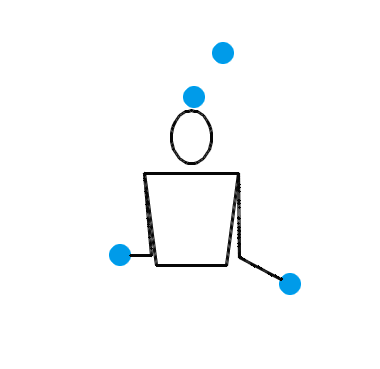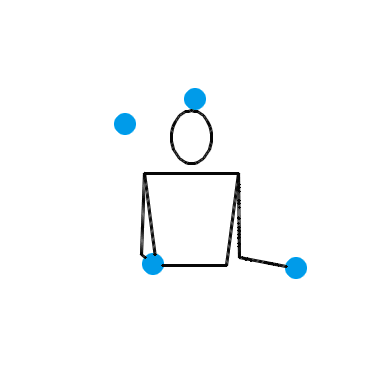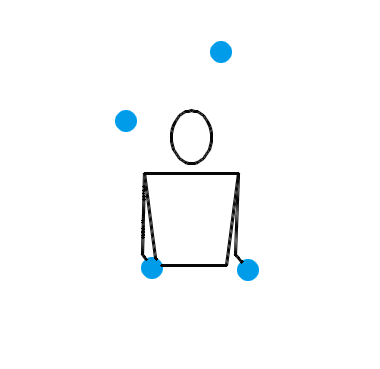
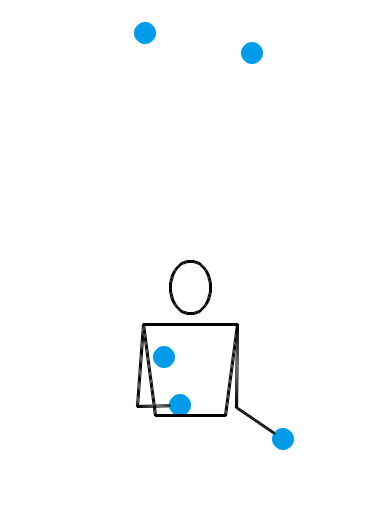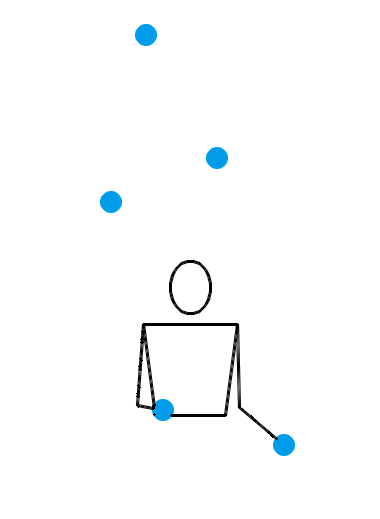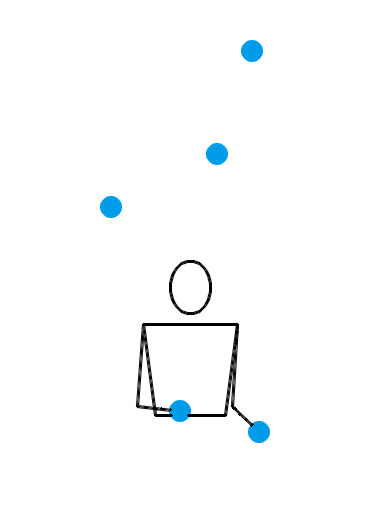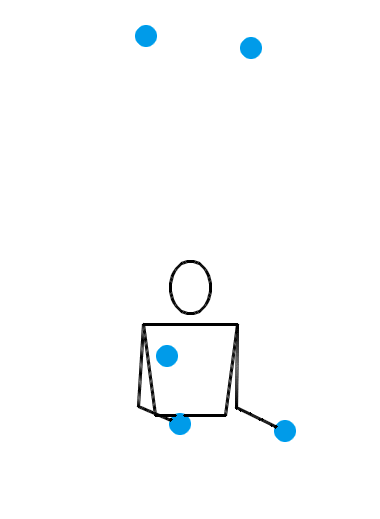
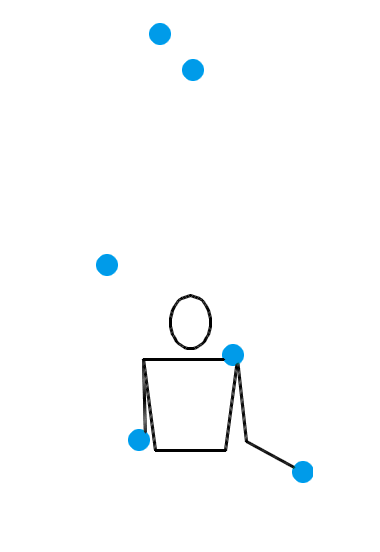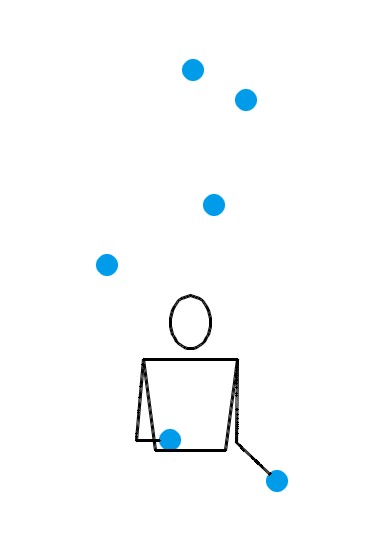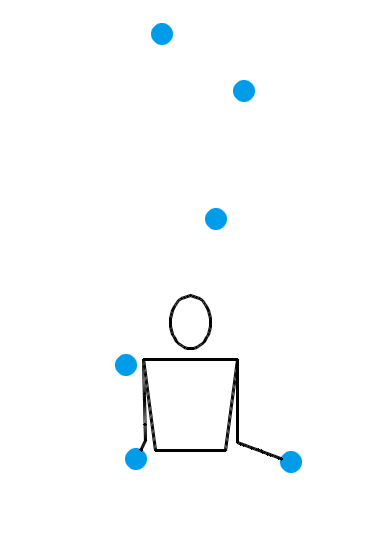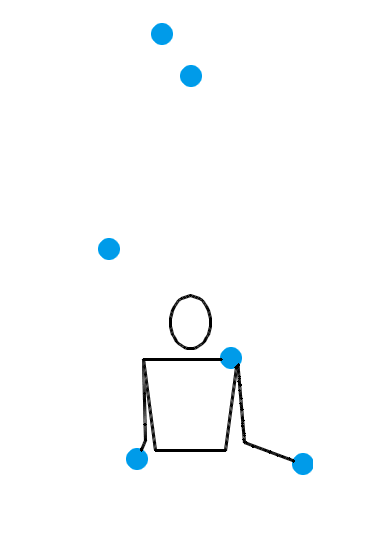
1995 年, Martin Probert 发明了一种生成新杂耍模式的傻瓜方法,其原理也可以用排列测试来解释。如果你想要一个循环节长度为 l 、小球数为 n 的新杂耍模式,你就可以先画一个 l × l 的方阵,然后在第 i 行第 j 列填入 n + i – j 的值。这相当于是在 l × l 的方阵的最左上角填一个 n ,然后按照向右走就减 1 ,向下走就加 1 的规律填充整个方阵。例如,我想要生成一个循环节长度为 5 、小球数为 4 的新杂耍模式,我画出的方阵就应该如左图所示:
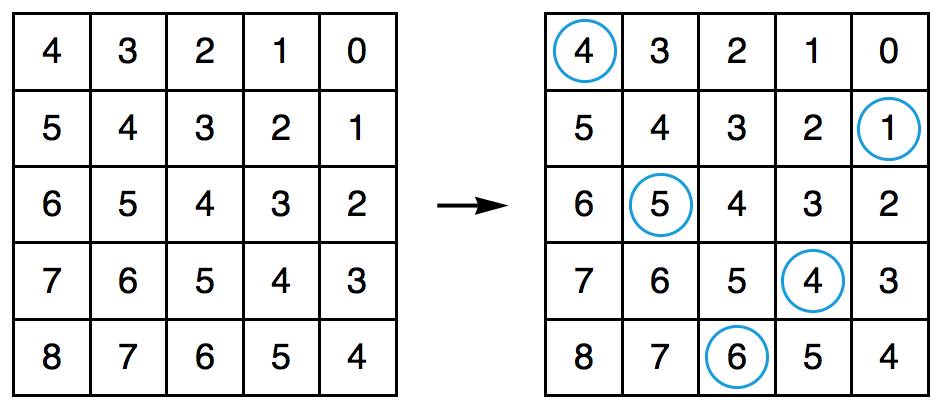
现在,从中任意选出 5 个方格,但要保证任意两个方格既不同行也不同列,如右图所示。接下来,从左至右读出各列的数字,于是得到 45641 。那么, 45641 就是一个合法的位换记号,并且它的长度为 l ,平均数为 n 。习惯上,我们会把 45641 写作 64145 ,以符合字典序最大的原则。
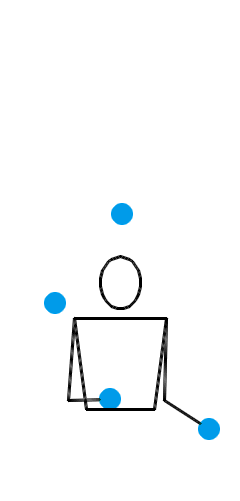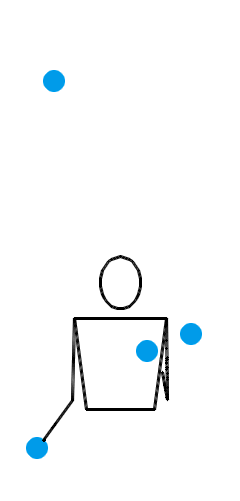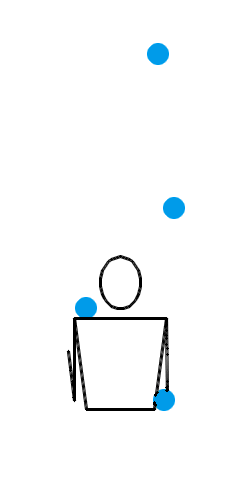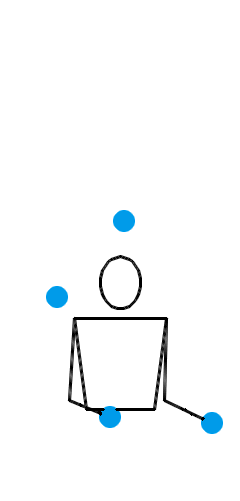
为了证明如此得到的数字串一定是合法的位换记号,我们只需要说明,如此得到的数字串一定能通过排列测试。也就是说,我们只需要说明,各列所圈的数字分别 +1, +2, …, +l ,除以 l 的余数正好取遍 0, 1, 2, …, l – 1 。为了给第 j 列所圈的数字 +j ,我们可以保持圆圈的位置不变,把这一列数整体循环上移 j 个单位,圆圈里的数就自动地 +j 了。当然,有时也不是真的 +j 了,比如把上图中的第 4 列循环上移 4 个单位,圆圈里的数会从 4 变成 3 ,而不是 8 。不过,这没关系,因为最后我们只关心它除以 l 的余数,只要它除以 l 的余数是对的就行了。然而,如果各列分别循环上移 1, 2, …, l 个单位后,方阵里的数除以 l 的余数就会形成这样的情况:一行全是 0 ,一行全是 1 ,一行全是 2 ,等等,一直到一行全是 l – 1 。所以,这些互不同行的圆圈,圈出的数除以 l 的余数正好取遍 0, 1, 2, …, l – 1 。
另外,我们选的这 l 个数的总和,相当于是 l 个 n 之和,再以某种顺序加上 1, 2, 3, …, l ,再以某种顺序减去 1, 2, 3, …, l 。因此,我们选的这 l 个数的平均数正好就是 n 。所以,利用 Martin Probert 的傻瓜方法,确实能够得到一个循环节长度为 l 、小球数为 n 的杂耍模式。
其实,如果知道了排列测试理论,我们还有更直接的办法来生成新的杂耍模式。对于任意正整数 l ,将 0, 1, 2, …, l – 1 随意地排成一排,各项依次减去 1, 2, 3, …, l ,然后每个地方都可以选择再加上任意一个 l 的整倍数(其中小于等于 0 的地方必须加到变正才行),如此得到的一定是合法的位换记号。枚举所有的可能性,我们就能得到所有合法的位换记号(可能会有重复)!可以说,我们终于有了一套描述、分析、生成杂耍模式的全套解决方案。
当然,位换记号并不能解决杂耍表演者会遇到的全部问题。试想,如果你玩了一段时间的 3 球瀑泻,想换一种 3 球玩法,但却不想停下重来。这就引出了一个问题:从 3 球瀑泻出发,能无缝切换到哪些其他的 3 球玩法,又该如何去切换呢?为了解决这类问题,人们发明了另一种强大的杂耍模式分析工具——状态图(state graph)。
让我们假设手上的小球永远是 3 个,并且位换记号涉及的数字最高到 5 (即一个小球最多在空中停留 5 拍)。我们可以认为,任何一个接抛动作完成的瞬间,所有 3 个小球就都在空中了;其中 1 个小球刚被抛起,其余小球则早已抛出,正处于上升或者下降的过程中。不管怎样,从此刻算起, 3 个小球落回手中所需要的拍数一定各不相同,并且都不会超过 5 。我们可以用一个 5 位 01 串来表示接下来这 5 拍的“占用”情况,数字 1 表示有小球会落回来,数字 0 表示没有小球会落回来。例如,如果完成某个接抛动作后, 3 个小球分别将在第 1 、 2 、 5 拍之后落回手中,我们就用 11001 来表示此时的状态。可以看出,在 3 球瀑泻中,完成任何一个接抛动作后,状态都是 11100 。
假设有 x 和 y 两个 01 串。把 x 的第一位去掉,再在最后面添一个数字 0 。如果此时 x 的第 h 位正好是数字 0 ,并且把它改为 1 之后,整个 01 串正好就变成 y 了,我们就说 x 可以通过动作 h 转换为 y 。它的直观意义就是,如果当前状态为 x ,那么下一个接抛动作可以是 h ,该动作完成后状态就会变成 y 。例如, 11100 可以通过动作 4 转换为 11010 ,也可以通过动作 5 转换为 11001 。
5 位 01 串中有 3 个数字 1 ,这一共有 C(5, 3) = 10 种可能性。让我们在纸上把这 10 种可能性全部写下来。如果某种状态能通过某个动作转换为另一种状态,我们就从前一种状态出发,画一根箭头指向后一种状态,并在路上标出动作的数值。注意,一个状态有可能转换为它本身,例如 11100 能通过动作 3 转换为它本身。我们就画一个箭头,从它出发,绕个小圈,指向它自己。另外,你会发现,以数字 0 开头的状态无法转移到任何其他状态,否则数字 1 的个数就不对了;更直观的说法则是,到了这种状态显然必死,因为下一拍就没有小球接了。
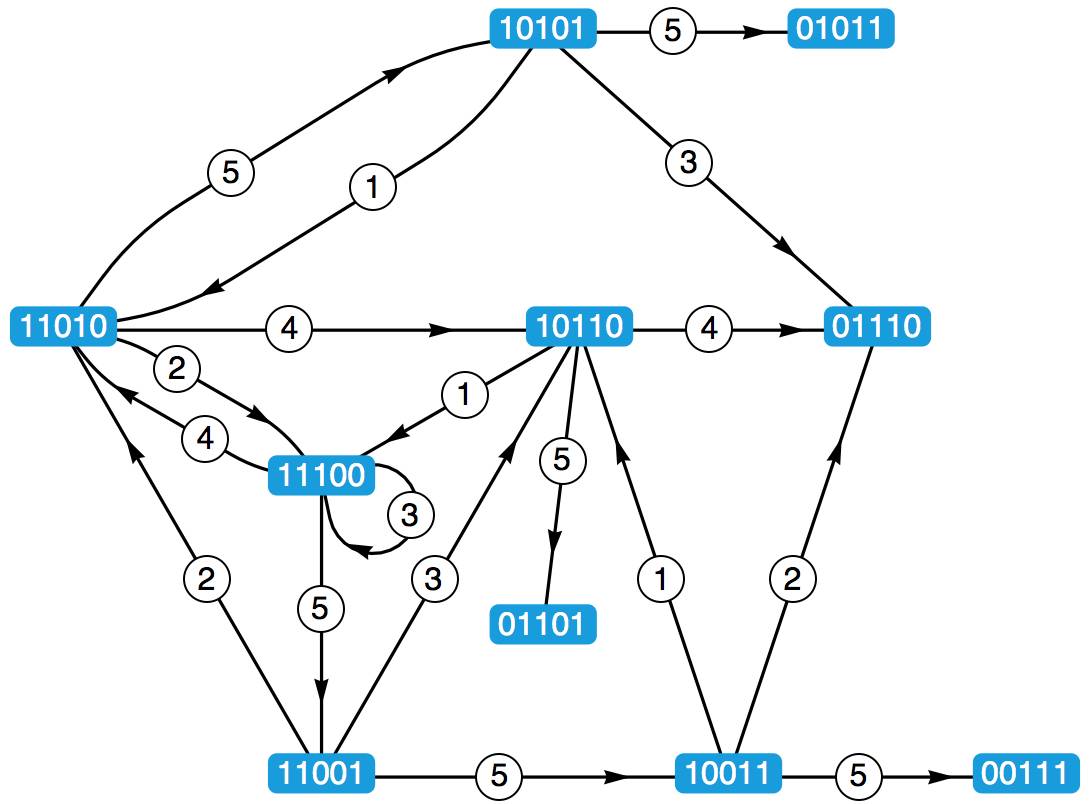
所以,只要沿着箭头走,路上经过的数字就自动地组成了合法的动作序列!而一个合法的位换记号,比如说 3 、 51 、 441 、 531 、 5313 等等,其实就是这个图上的回路!杂耍模式之间的衔接问题,也就解决了:我们只需要看看,能否从前一个回路的某个节点出发,沿着箭头走到另一个回路里去。比方说,你本来玩着 3 球瀑泻,突然想玩 3 球倾盆了。于是,你可以用动作 4 进行衔接,按照 33…345151…51 的规律抛球。什么时候你又想回到 3 球瀑泻的玩法,你就可以用动作 2 进行衔接,按照 5151…51233…3 的规律抛球。当然,你也可以用动作 41 进行衔接,按照 5151…514133…3 的规律抛球。下图所示的就是位换记号 333451515141 (这次我们有意没按字典序最大原则对其进行重写)及其演示动画,它就是由 3 球瀑泻和 3 球倾盆组成的大循环,中间分别以 4 和 41 衔接。
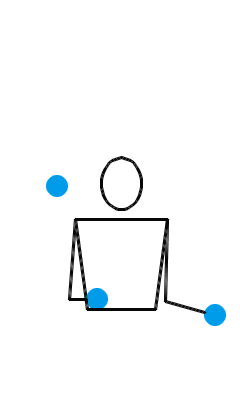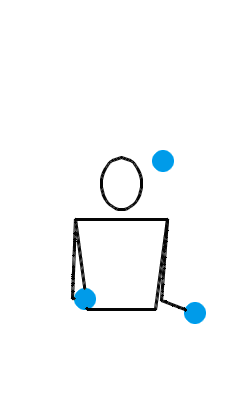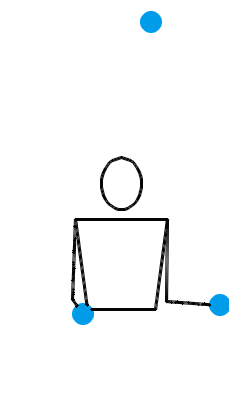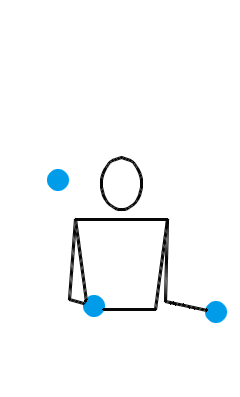
用这种方法,我们可以搞出像 333451515141 这样很长很长,很复杂很复杂,却没啥实质意义的位换记号——它仅仅是由一些更基本的位换记号拼成的。
在状态图中,如果一条回路经过了某个重复的节点,我们就可以把它视作两个以该节点为公共节点的小回路。如果某个小回路仍然经过了重复的节点,我们还可以继续把它分解成两个更小的回路,直到每个回路都被分到不可再分(即都分到不再经过重复的节点)。
如果一个位换记号在状态图中不会经过重复的状态,我们就说这是一个“素位换记号”(prime siteswap)。根据上述推理,如果一个位换记号不是素位换记号,那么它一定能看作是由若干个素位换记号组合而成的。例如, 333451515141 就是由三个 3 、三个 51 和一个 441 组成的。我们前面提到过 531333…33 的模式,其实也就是由一个 531 和任意多个 3 组成的。
正如化学元素按一定规律适当组合后,可以得出千千万万的物质一样,素位换记号按一定规律适当组合后,也会得出千千万万的杂耍模式。也就是说,素位换记号对应着杂耍模式的基本组成单元。从这个意义上说,寻找所有的素位换记号,比生成所有合法的位换记号更为重要。为了找出所有的素位换记号,我们只需要在状态图中找出所有不经过重复节点的回路。当小球数为 3 时,所用数字不超过 5 的素位换记号一共有 8 个,它们是:
3, 42, 51, 441, 522, 531, 5241, 5511
把它们掌握了之后,就能变幻出形形色色更复杂的杂耍模式了。
我们从几个最基本的杂耍模式,说到了位换记号与平均数定理,说到了排列测试与位换记号的生成方法,说到了状态图与素位换记号。但是,刚才的一切仅仅是假设,左右两只手是在交替地接抛一个又一个的小球。如果两只手是同步运作的呢?或者,如果每次可以接抛不止一个小球呢?或者,如果我们有两个杂耍者,他们互相之间还能把小球扔给对方呢?我们又应该用什么记号来表示它们呢?刚才提到的结论能否继续扩展到这些情况呢?感兴趣的朋友不妨看看 Burkard Polster 的 The Mathematics of Juggling 一书。这篇文章中的内容主要也都是从这本书里来的。
整篇文章以视频开头,不妨让我们以视频结尾吧。最后这个视频来自 https://www.youtube.com/watch?v=e5E84ePfEOw 。看了这个视频后你就会了解到,这篇文章探讨的,真的只是最基本最基本的杂耍而已。














