
【美东时间2月28日晚9点,北京时间3月1日上午10点,网络公开讲座,有兴趣参加者,请登陆网址:https://learn.xnextcon.com 进行报名。 】
纽约的气候四季分明,冬去春来,万物复苏。作为国际大都市,纽约的常驻人口汇集了全世界几乎所有的民族,流动人口异常庞大,宾夕法尼亚车站每天任何时刻都是熙熙攘攘,人声鼎沸。曼哈顿岛上高耸入云的摩天大厦,鳞次栉比,地面上车水马龙,川流不息。食肆酒吧,剧院商铺,琳琅满目,极尽繁华。在人口密度如此之高的小岛上,各色病毒也在肆虐生长,繁殖变异。每一年的暖冬,就意味着来年春季的流感大爆发。
每年开春,纽约地区都有流感袭击,一如四季轮回,今年依然来势凶猛。因为病毒产生了新的变异,市面上除了流感疫苗,并没有什么特效药,只能依靠自身的免疫系统来抵抗。每年流感都有不同症状,身体的所有器官系统渐次被侵袭,逐步自愈,最后锁定在最为脆弱的系统中进行持久斗争。作为教师,终日与黑板粉尘为伍,最为脆弱的器官自然是上呼吸道。在耐心等待自愈期间,只能多喝开水、多冲热水澡,同时潜下心来思考一些数学问题。
自然数据具有内在的模式,深度学习方法可以有效地揭示这些模式,因而取得了巨大的成功。数据中一种普适的模式可以被概括为
流形分布定律
:一类自然数据分布在高维背景空间中的低维流形附近。因此,数据可以用流形上的概率分布来描述。深度学习具有两个基本任务:流形学习,以及概率分布之间的变换。概率分布变换可以用经典的最优传输理论来完成。
例如GAN中的生成器本质上是将高斯分布变换成实际数据分布,判别器本质上计算两个分布之间的距离。最优传输理论的核心问题就是计算概率分布之间的变换,其代价用于衡量概率分布之间距离。
依随深度学习方法的日益深入人心,大众对最优传输理论的学习热情也日益高涨。最优传输理论具有丰富的内涵,同时也是众多领域交汇的地带,例如概率统计、微分几何、流体力学、线性规划、蒙日-安培方程等等。不同的方法各有千秋,有些易于理解,有些易于计算,有些偏几何洞察,有些偏物理直觉。比如,对于深度学习而言,基于Minkowski-Alexandrov理论的
凸几何解释
非常适于GPU实现;对于对抗生成网络的
模式崩溃
问题,基于蒙日-安培方程的正则性理论给出了颇有说服力的解释;对应医学图像的注册问题,流体力学方法应用最多。这里,我们比较几何方法和流体力学方法,从而得到更为深刻的理解。
假设
 和
和
 是
是
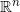 中的两个概率分布,具有概率密度
中的两个概率分布,具有概率密度
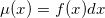 ,
,
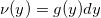 ,并且满足足够的光滑性条件。我们可以想象
,并且满足足够的光滑性条件。我们可以想象
 和
和
 代表了空间某种特殊气体的质量分布,
代表了空间某种特殊气体的质量分布,
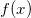 和
和
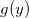 给出了这种物质的密度。给定一个光滑的双射(微分同胚),
给出了这种物质的密度。给定一个光滑的双射(微分同胚),
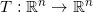 ,那么微分同胚会带来体积元的变化,从而改变了特殊气体的密度。如果微分同胚将概率分布
,那么微分同胚会带来体积元的变化,从而改变了特殊气体的密度。如果微分同胚将概率分布
 变成了概率分布
变成了概率分布
 ,等价的,微分同胚将密度
,等价的,微分同胚将密度
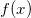 变成了
变成了
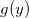 ,即
,即
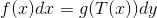
那么我们说传输映射
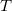 保测度,记成
保测度,记成
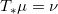 。相应的偏微分方程为雅可比方程:
。相应的偏微分方程为雅可比方程:
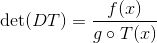 。
。
假设
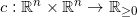 为传输代价函数,
为传输代价函数,
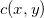 代表运输单位质量从
代表运输单位质量从
 点到
点到
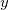 点的代价。一个传输映射的传输代价为
点的代价。一个传输映射的传输代价为
 。
。
蒙日(Monge)提
出了最优传
输问题如下:在所有保测度的传输映射中,寻找传输代价最小者,即
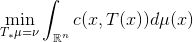 。
。
蒙日问题的解被称为是
最优传输映射
,最优传输映射的传输代价被称为是两个概率分布之间的Wasserstein距离,
 。
。
Brenier理论表明,如果传输代价为欧氏距离的平方,
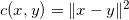 ,那么存在一个凸函数,
,那么存在一个凸函数,
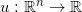 ,被称为是Brenier势能函数。Brenier势能函数的梯度映射给出了最优传输映射,
,被称为是Brenier势能函数。Brenier势能函数的梯度映射给出了最优传输映射,
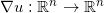 ,并且Brenier势能函数彼此相差一个常数,最优传输映射唯一。将雅可比方程中的
,并且Brenier势能函数彼此相差一个常数,最优传输映射唯一。将雅可比方程中的
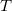 替换成梯度映射
替换成梯度映射
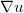 ,那么我们得到经典的蒙日-安培方程:
,那么我们得到经典的蒙日-安培方程:
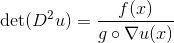 。
。
蒙日-安培方程和经典的Minkowski问题紧密相连,Minkowski问题是从高斯曲率和法方向重建曲面。因此蒙日-安培方程可以用
几何方法
来解,并且在深度学习上已经应用。

图1. 几何方法计算的最优传输映射。
如果目标区域非凸,则Brenier势能函数依然连续,但是最优传输映射非连续,这造成了模式崩溃问题。

图2. 从实心球到兔子的最优传输映射的非连续点集合(苏科华作)。
由Brenier梯度映射,我们可以构造一族概率测度和相应的最优传输映射
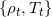 ,
,
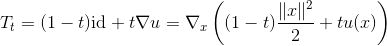 ,
,
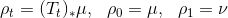 .
.
我们可以证明,对于任意的
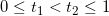 ,传输映射
,传输映射
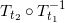 是从
是从
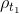 到
到
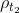 的最优传输映射。
的最优传输映射。
流体力学的观点更符合物理直观。我们考察特殊气体在空间的流动。从宏观上看,在时刻
 ,空间点
,空间点
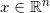 处的气体密度为
处的气体密度为
 。从欧拉观点来看,每个气体粒子的运动轨迹为一条空间曲线。假设起始点为
。从欧拉观点来看,每个气体粒子的运动轨迹为一条空间曲线。假设起始点为
 的粒子轨迹为
的粒子轨迹为
 ,
,
 。如果不同粒子的轨迹在某个时刻相交,那么宏观上流场出现激波(shock)。我们假设没有激波出现,那么在时刻
。如果不同粒子的轨迹在某个时刻相交,那么宏观上流场出现激波(shock)。我们假设没有激波出现,那么在时刻
 ,每个粒子的初始位置映射到当前位置,我们得到全空间的整体微分同胚:
,每个粒子的初始位置映射到当前位置,我们得到全空间的整体微分同胚:
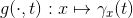 。
。
在时刻
 ,粒子的速度向量为
,粒子的速度向量为
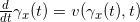 。这一时刻,全空间的整体速度场表示为
。这一时刻,全空间的整体速度场表示为
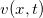 ,那么微分同胚满足常微分方程:
,那么微分同胚满足常微分方程:
 .
.
如果给定速度场
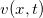 ,我们可以得到相应的微分同胚群
,我们可以得到相应的微分同胚群
 。换言之,如果速度场
。换言之,如果速度场
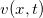 足够光滑,那么流场不会出现激波。
足够光滑,那么流场不会出现激波。
空间每一点密度的变化满足散度方程:
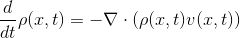 ,
,
在这一时刻,所有粒子的动能为:
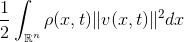 .
.
我们考察所有联结
 和
和
 的流场构成的空间,我们将
的流场构成的空间,我们将
 简写成
简写成
 ,则
,则















