太长不看版
量化文生图扩散模型的成功范式。
Diffusion Model 的部署一直都是个很大的问题,因为随着这种模型越做越大就需要更多的 memory 造成更大的时延,而这些对于部署而言都是不利的。
本文给出了一个很激进的量化方案:
把扩散模型的 weight 和 activation 都量化为 4 bit。
在如此激进的量化层面上,weight 和 activation 都高度敏感,传统 LLM 的 post-training quantization 方法,如 smoothing 就不好使了。
因此,本文提出了一种 4-bit 量化算法:SVDQuant。SVDQuant 的核心操作不像 smoothing 那样在 weight 和 activation 之间重新分配异常值 (Outlier),而是使用一个 low-rank 分支来吸收这些异常值。SVDQuant 首先通过将异常值从 activation 转移到 weight 来巩固异常值,然后使用高精度的 low-rank 分支通过奇异值分解 (SVD) 获取权重异常值。这个过程使得 weight 和 activation 的量化都得到了简化。但由于激活的额外数据移动,简单地独立运行 low-rank 分支会产生显著的额外开销,使得量化很难获得实际加速。
为了解决这个问题,本文 co-design 了推理引擎 Nunchaku,把 low-rank 分支的 kernel 吸收到 low-bit 分支中,切断冗余的内存访问。它也可以无缝支持现成的低秩适配器 (LoRA),而无需重新量化。作者在 SDXL, PixArt-Σ, 和 FLUX.1 上都进行了实验。12B FLUX.1 模型的内存使用量减少了 3.5 倍,在 16GB 笔记本电脑 4090 GPU 上的 4-bit权重量化基线上实现了 3.0 倍的加速。
 图1:SVDQuant 是一种训练后量化,用于 4 bit 权重和激活,可以很好地保持视觉保真度。在 12B FLUX.1-dev 上,与 BF16 模型相比,它减少了 3.6 倍的 memory。通过消除 CPU offloading,在 16GB 笔记本电脑 4090 GPU 上时,它比 16 bit 模型提供了 8.7 倍的加速,比 NF4 W4A16 基线快 3 倍
图1:SVDQuant 是一种训练后量化,用于 4 bit 权重和激活,可以很好地保持视觉保真度。在 12B FLUX.1-dev 上,与 BF16 模型相比,它减少了 3.6 倍的 memory。通过消除 CPU offloading,在 16GB 笔记本电脑 4090 GPU 上时,它比 16 bit 模型提供了 8.7 倍的加速,比 NF4 W4A16 基线快 3 倍
下面是对本文的详细介绍。
本文目录
1 SVDQuant:吸收异常值量化 4-bit 扩散模型
(来自 MIT 韩松团队,NVIDIA)
1 SVDQuant 论文解读
1.1 SVDQuant 研究背景
1.2 量化过程介绍
1.3 问题定义
1.4 SVDQuant 方法介绍
1.5 推理引擎 Nunchaku
1.6 SVDQuant 支持的模型数据集和评价指标
1.7 实验结果
1
SVDQuant:吸收异常值量化 4-bit 扩散模型
论文名称:SVDQuant: Absorbing Outliers by Low-Rank Components for 4-Bit Diffusion Models
论文地址:
http://arxiv.org/pdf/2411.05007
Quantization Library:
http://github.com/mit-han-lab/deepcompressor
Inference Engine:
http://github.com/mit-han-lab/nunchaku
1.1 SVDQuant 研究背景
扩散模型通过在海量数据上进行训练,可以从简单的文本提示生成令人惊叹的图像。为了追求更高的图像质量和更精确的文本到图像对齐,研究者开始扩大扩散模型。Stable Diffusion 1.4 只有 800M 参数,而 SDXL 扩展到 2.6B 参数。AuraFlow v0.1[1]进一步扩展为 6B 参数,最新模型 FLUX.1[2]扩展到了 12B 参数。如图2所示,与大语言模型 (LLM) 相比,扩散模型的计算量要大得多。它们的计算成本随模型大小的增加而迅速增加,给现实世界的模型部署带来了令人望而却步的内存和时延障碍,特别是对于需要低延迟的交互用例。
 图2:LLM 和扩散模型的计算量 vs. 参数量。LLM 的计算是用 512 的 context 和 256 输出 tokens 来衡量的,扩散模型的计算是针对单步的
图2:LLM 和扩散模型的计算量 vs. 参数量。LLM 的计算是用 512 的 context 和 256 输出 tokens 来衡量的,扩散模型的计算是针对单步的
由于摩尔定律放缓,硬件供应商转向低精度推理以维持性能提升。例如,NVIDIA 的 Blackwell Tensor Cores 引入了一个新的 4-bit floating point (FP4) 精度,与 FP8 相比,性能翻倍。因此,使用 4-bit 推理来加速扩散模型很有吸引力。在 LLM 领域,研究人员利用量化来压缩模型大小并提高推理速度。
但是,扩散模型与 LLM 不同,LLM 的时延主要受权重加载的限制,对于小 Batch size 的扩散模型计算量仍然很大。仅仅量化权重不可以加速扩散模型。为了实现加速,weight 和 activation 必须量化为同等位宽。否则,较低精度的计算性能优势将被抹除。
因此,本文专注于将扩散模型的 weight 和 activation 量化为 4 bits。这种具有挑战性和激进的方案往往容易出现严重的质量下降。本文提出了一种新的通用量化范式 SVDQuant。
其可以用下图3概括。SVDQuant 的核心思想是引入一个低成本的分支来吸收两边的异常值。为了实现这一点, 首先通过平滑将它们从激活
迁移到权重
来聚合异常值。然后将奇异值分解 (SVD) 应用于更新的权重
, 将其分解为低秩分支
和残差
。low-rank 分支以 16-bit 运行, 允许仅将残差量化为 4 位, 这显着减少了异常值幅度。
 图3:SVDQuant 方案。(a) 最初,激活 X 和权重 W 都包含异常值,这使得 4 位量化具有挑战性。(b) 将异常值从激活迁移到权重,从而得到新的激活和权重。虽然新的激活更容易量化,但新的权重现在变得更加困难。(c) SVDQuant 进一步将权重分解为低秩分支和残差分支。低秩分支 16 位运行,减轻了量化难度
图3:SVDQuant 方案。(a) 最初,激活 X 和权重 W 都包含异常值,这使得 4 位量化具有挑战性。(b) 将异常值从激活迁移到权重,从而得到新的激活和权重。虽然新的激活更容易量化,但新的权重现在变得更加困难。(c) SVDQuant 进一步将权重分解为低秩分支和残差分支。低秩分支 16 位运行,减轻了量化难度
但是直接运行 low-rank 分支会产生大量的内存访问开销,抵消了 4-bit 推理加速。为了克服这个问题,我们一起设计了一个专门的推理引擎 Nunchaku,将低秩分支计算融合到 4-bit 量化和计算 Kernel 中。这种设计能够在有额外的分支的情况下实现推理加速。
1.2 量化过程介绍
量化是加速网络中线性层的有效方法。给定一个张量
,量化过程定义为:
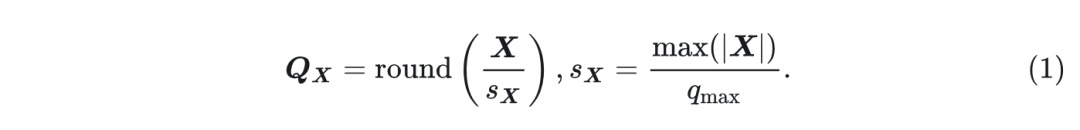
式中,
是
的 low-bit 表示,
是比例因子,
是最大量化值。对于有符号的
位整数量化,
。对于 1 位尾数和 2 位指数的 4 位浮点量化,
。因此,去量化张量可以表述为
。对于输入
和权重
的线性层, 其计算可以近似为:
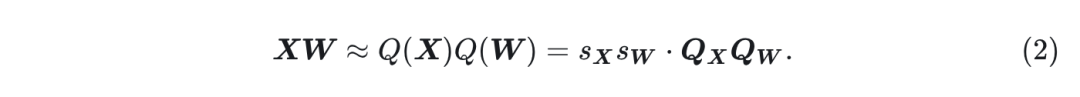
相同的近似适用于卷积层。为了加快计算速度, 现代算术逻辑单元需要具有相同位宽的
和
。
本文专注于用于加速的 W4A4 量化,其中权重和激活的异常值都有很大的障碍。抑制这些异常值的传统方法包括量化感知训练 (QAT)[3]和 Rotation[4][5][6]。QAT 需要大量的计算资源,特别是对于超过 10B 参数的模型 (例如,FLUX.1)。由于扩散模型中使用自适应归一化层,Rotation 不适用。归一化权重由于需要运行时候在线生成,所以没办法离线集成到投影层权重里。所以,在线生成的激活和权重都会产生显著的计算开销。
1.3 问题定义
SVDQuant 的核心思想是引入额外的 low-rank 分支,可以吸收 weight 和 activation 中的量化困难。最后,作者提供了一个具有 Kernel 融合的协同设计推理引擎 Nunchaku,以最小化 4 bit 模型中 low-rank 分支的开销。
设线性层为
, 权重为
, 则量化误差为:
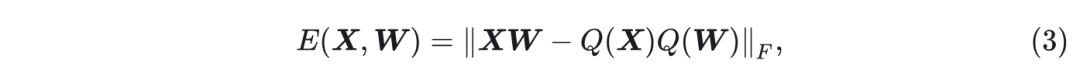
式中,
是 Frobenius 范数。
Proposition 1 (误差分解):
量化误差可以分解为:
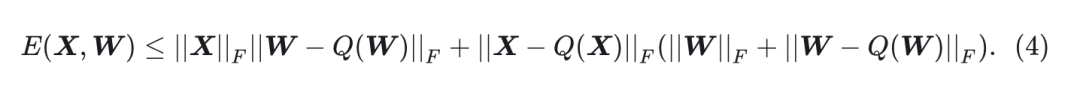
从命题中可以看出, 误差受权重和输入的大小
以及它们各自的量化误差
的限制。为了最小化整体量化误差, 目标是优化这4项。
1.4 SVDQuant 方法介绍
Smoothing 是减少异常值的有效方法。可以通过缩小输入
并使用每通道平滑因子
相应地调整权重矩阵
来平滑激活中的异常值。如图 4(a)(c) 所示, 平滑输入
表现出减小的幅度和更少的异常值,从而导致较低的输入量化误差。然而,在图 4(b)(d) 中,转换后的权重
在幅度和异常值的存在方面都显着增加,这反过来又提高了权重量化误差。因此,整体误差减少有限。
 图4:PixArt-Σ 中输入和权重的示例值分布,λ 是平滑因子,红色表示异常值。最初,权重和激活值都包含大量异常值。Smoothing 之后,激活的异常值减少,权重展示出更多异常值。减去 SVD low-rank 分支之后,剩下的部分的范围更窄,并且不受异常值的影响
图4:PixArt-Σ 中输入和权重的示例值分布,λ 是平滑因子,红色表示异常值。最初,权重和激活值都包含大量异常值。Smoothing 之后,激活的异常值减少,权重展示出更多异常值。减去 SVD low-rank 分支之后,剩下的部分的范围更窄,并且不受异常值的影响
用 low-rank 分支吸收增加的权重异常值。
本文核心的做法是引入一个 16-bit low-rank 分支, 并进一步将权重量化难度迁移到该分支。具体来说,将转换后的权重分解为
,其中
和
是秩
的两个低秩因子,
是残差。那么
可以近似为:
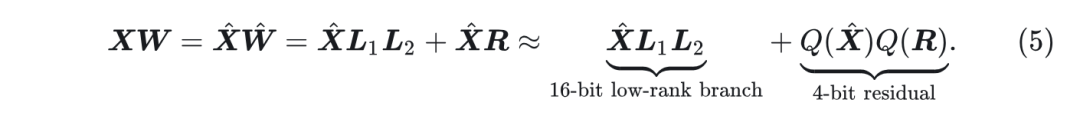
与直接进行 4-bit 量化, 即
相比, 本文的方法首先以 16-bit 精度计算 low-rank 分支
, 然后用 4-bit 量化逼近残差
。实践中, 一般设置
, 通常为 16 或者 32。因此, low-rank 分支的附加参数和计算可以忽略不计。现在, 仍然需要仔细的系统设计来消除冗余内存访问。
根据上式5,量化误差可以写成:
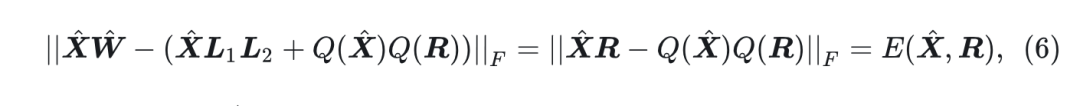
根据命题 4.1, 由于
已经没有异常值, 因此只需要专注于优化
及其量化误差
Proposition 2 (量化误差界):
对于式1 中描述的任何张量
和量化方法,如
。假设
的元素服从正态分布, 则有:
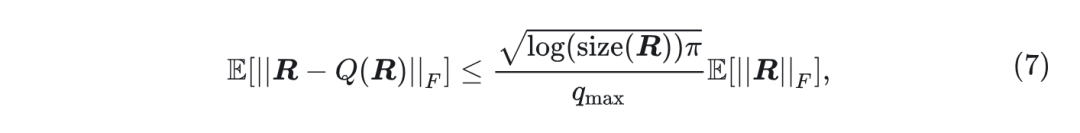
其中
表示
中的元素数。
因此,量化误差
受残差
大小的限制。
因此,本文目标是找到使
最小化的最优
,这可以通过简单的奇异值分解 (SVD) 来解决。给定
的 SVD,最优解为
图5 绘制了原始权重
、转换后的权重
和残差
的奇异值分布。原始权重
的奇异值高度不平衡。平滑后,转换后的权重
的奇异值分布更加陡峭,前几个值明显更大了。
 图5:不同变量的前 64 个奇异值分布。转换后的矩阵的前 32 个奇异值表现出陡峭的下降,而其余的值更渐进
图5:不同变量的前 64 个奇异值分布。转换后的矩阵的前 32 个奇异值表现出陡峭的下降,而其余的值更渐进
通过去除这些主导值, Eckart-Young-Mirsky 定理表明残差
的大小显着降低。因为有
, 原始的幅值为
, 其中
为
的第
个奇异值。
此外, 实践表明, 与
相比,
表现出更少的异常值, 具有显着压缩的值范围, 如图 4(d) (e)所示。在实践中,可以通过分解
并相应地调整
多次迭代来进一步减少量化误差,然后选择误差最小的结果。
因此,SVDQuant 的思路:
-
原始模型中,根据 Proposition 1 得到的误差分为 4 项,都要考虑。
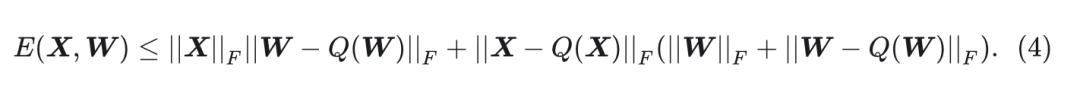
-
使用了 Smoothing 操作之后, 此时
已经基本没有异常值了, 但是此时
中的异常值加剧。还是不好。
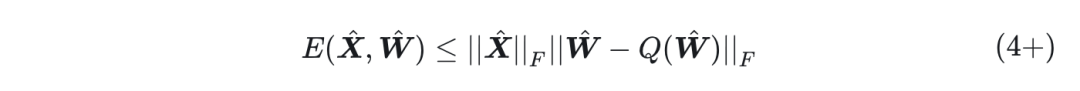
-
使用了本文提出的 low-rank 分支之后,将误差表达式变为了 5 式,继而将量化误差等效为 7 式 (由于此时
已经基本没有异常值了)。
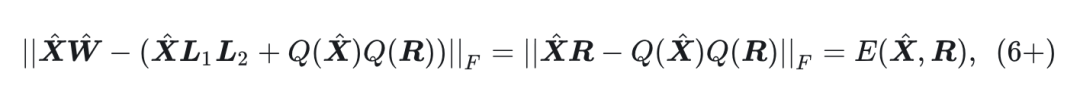
-
根据 Proposition 2 得到 7 式的量化误差相当于以残差















