好书推荐 | 《不一样的数学题》：江苏省初中数学文化节试题精编与品评

2019年的全国高考数学卷中，有两题令人眼前一亮。

全国1卷理科数学第4题：

全国1卷理科数学第6题

第4题以“断臂维纳斯”为例，探讨了黄金分割之美，第6题以我国古代典籍《周易》中的“卦”为背景设置了排列组合问题。这类以数学文化为背景的试题是今年高考的一大亮点，也成为了人们津津乐道的话题，而这种趋势正在逐渐向中考蔓延。究其原因，乃是新课程标准对数学文化的重视。

《全日制义务教育数学课程标准（实验稿）》明确指出：数学文化作为教材的组成部分，应渗透在整套教材中。为此，教材可以适时地介绍有关背景知识，包括数学在自然与社会中的应用、以及数学发展史的有关材料，帮助学生了解在人类文明发展中数学的作用，激发学习数学的兴趣，感受数学家治学的严谨，欣赏数学的优美。

数学不只有公式、定理和无休止的运算，它还蕴含人文素养、理性精神、思想方法。 在数学教育中渗透数学文化教育是数学教育发展的趋势，以数学文化为背景命制试题将成为中、高考的一大热点。将经典文化融入试题当中，既普及知识，又灵活考查了同学们的阅读、理解和应用能力。这也是核心素养背景下的数学教学所强调的，颇具引领作用。

那么数学文化怎么考呢？很多学生和教师颇感迷茫。

长期关注“ 好玩的数学 ”公众号的读者一定还记得四年前我们给大家推荐的一本书—— 《江苏省初中数学文化节试题精编与品评》 。

戳此查看>> 应试教育里的一朵奇葩，一本值得您收藏的书！

该书收录了 江苏省初中数学文化节 从2005年至2014年10年的全部试题，所有的试题皆是以数学文化为指导进行命制。

在此有必要简单介绍一下江苏省初中数学文化节， 江苏省初中数学文化节 是2005年由《时代学习报》编辑部和江苏省教育学会中学数学教学专业委员会联合举办的数学文化活动，活动旨在更好地传播优秀数学文化，培养青少年的数学兴趣和素养，提高数学思维和解题能力。至今，文化节已成功举办了 14届 ，每年均有十多万同学参加，深得师生、家长喜爱，也备受教育教研部门的重视。但是这项活动很多人并不一定知道，主要是因为数学文化节主要在江苏省范围内举行。

今年（2019年），《江苏省初中数学文化节精编与品评》的升级版 《不一样的数学题——初中数学文化节精编与品评》 重磅推出，该书将前14届数学文化节试题全部收录其中。此书不仅可以作为将来参加数学文化节的学生的参考资料，对于数学教师、数学文化研究者、爱好者都具有极高的研究和收藏价值。

旧版《江苏省初中数学文化节精编与品评》以“数学之史”、“数学之美”、“数学之思”、“数学之用”、“数学之语”为板块对试题进行分类汇编，新版《不一样的数学题》按初中知识板块和学习进度作了分类汇编，更有利于学生学习和教师教学参考之用。

新版的参考答案另外成册，既有详细解答，又有精彩品评，方便查询。

江苏省初中数学文化节将用14年的经验和积累告诉我们“数学文化怎么考”，“数学文化试题如何命制”。

沙国祥主编和张磊在《数学文化活动的问题设计》一文中 （见该书附录） 总结了数学文化问题设计的立意与架构，对于“数学文化怎么考”具有很好的指导意义。

1. 取材广泛，给学生一个宏大的视野

初中数学文化节的问题设计，涉及古今中外、自然社会中一切与数学相关的题材，尤其是日常生活中不易想到与数学竟然有关的地方，更是数学文化节试题关注的焦点，以此引发学生的好奇和兴趣。

比如第2届第二轮第16题，介绍了神奇的“ 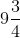站台”：

第3届第一轮一道关于书画装裱尺寸比例的问题，反映了艺术美与比例和谐之间的关系：

第10届第二轮第10题引自当年最新报道，希望学生用数学分析投票中的问题：

另外，还值得一提的是，在参加历届数学文化节的学校，第一轮活动中所有学生均参加，而不只是少数数学上有特长的学生才有资格，因此， 数学文化节活动绝不是奥数比赛，这本书中的试题也绝不是奥数试题，这项活动是面向将来可能从事各种职业的学生，这本书适合所有的学生。

2. 意味深长，让学生深入理解数学文化内涵

数学问题的设计，由表及里，深入到数学文化的核心层，展示数学内在的精神、方法、魅力，突出对数学内涵和魅力的深度揭示，而非浮于表面，仅图个热闹好玩。

比如“对称”，初中往往只止步于“折叠后”的图形的重合，对于对称思想、对称美的揭示还处于表层的操作活动，而对称是一种深刻的数学思想和美的形式，贯穿于几何、代数、概率中，在物理、化学、生物、经济、文学、艺术等领域都有着对称的身影。

如首届第二轮第5题介绍了与文学有关的对称问题：

3. 淡化技巧，引学生走上数学大道

人类文化，只有摆脱个体自身的偏见，才能发现客观规律和普遍模式，有利于文化传播和共享。物理学上，牛顿的万有引力定律，解释了苹果、月球受到地球的引力，行星围绕太阳的运动，都符合同一规律；数学上，笛卡儿、费马创立的解析几何，倡导代数抽象与几何直观相结合的大道通法，原则上藉此可解决任何几何问题，可以用方程研究曲线。“微积分就是从这个系统发展而来的，其他科学家和数学家对这种技术的采用立刻就以不可逆转的方式推进了数学在全世界的普及，从而永久地改变了西方数学。”

因此，在设计数学文化问题时，要引导学生领悟数学大道，倡导通性通法。如第10届数学文化节第8题：

4. 注重感悟，为学生营造数学文化氛围

文化的浸润是通过感悟悄然进行的，数学文化节试题的设计，要留给学生感悟的题材，创设数学文化氛围。粗浅的感悟是对问题的浏览、观察、操作、演算等，直观感受到问题包含的知识以及题面的有趣、漂亮、新颖，引发好奇心；进一步的感悟是细读、理解、联想、分析等，运用数学的知识和方法解决问题，感受数学的力量和应用价值；再深层次，可以领悟以至顿悟到试题中蕴含的数学思想和数学美，看出数学试题的背景和来龙去脉。

例如，第5届七年级第一轮第3题，意在引发学生初步感受上海世博会建筑艺术设计所呈现的数学图形美（外在美）：

第5届第二轮第4题，则让学生在计算比例大小的过程中感悟艺术设计的和谐美（内在美）：

第2届第一轮第5题，题材虽然并不新鲜，但可以让学生透过题面似乎夸张的语言表述：“它的周长可以大于地球的赤道长，甚至可以大于地球到月亮、太阳的距离……”，感悟雪花分形的奇特性质：

5.形式多样，辐射出数学文化的美丽芬芳

（1）设置题头提示语。为了帮助学生深入理解、感悟数学文化，启发、优化思维，在解答问题后有更多收获，体现命题者对学生深切的人文关怀，在每个问题前加了言简意赅的导语，如“无穷探索”“01定乾坤”“幸运52”“对称与对仗”等，或揭示问题的数学内涵、特点，或展示数学的美妙、价值，或提示思路、策略，提醒注意思维严谨等。

（2）将解题与阅读、写作相结合。数学文化节大多试题的题面并非纯数学题的干巴巴的常见形式——“条件加结论”，而往往包含丰富的阅读材料、背景解说和动机描述；另外，七年级第一轮活动甚至要求学生写一篇300字长、运用某些关键词的小作文，如第3届第一轮最后一题：

数学考试中还有作文题，是不是既新鲜又有趣？

（3）第一轮与第二轮试题的呼应。一些相关的问题在第一、第二轮活动中以不同层面、不同深度呈现，从知识、思维、方法到观念、精神，从表层现象到内在本质，从直观感受到理性认识，从结果到过程、联系，从继承、发展到创新，由浅入深地加以探究，让学生逐步体味问题的本质、方法的精髓、思想的核心。

例如，第8届数学文化节八年级试题第一轮的第9题：

在本届第二轮活动中，结合了第1题，上述问题便演变为第11题：

利用第1题的结论，将计算四边形KHCF的面积转化为求正方形AEKG的面积，然后运用第一轮第9题的方法即可。

（4）部分题目设计成题组形式。此举意在营造文化氛围，引导学生探究数学问题，揭示数学与人类文化的内在联系。如第9届数学文化节八年级第二轮最后一题（第15题），从恒大足球队的海报引出拉马努金公式的原理和包含五个基本数学常数学的欧拉公式，进而联想到简单多面体的欧拉公式，并用于研究确定普通足球面上的五边形、六边形的个数，将相关问题通过足球这条纽带串联起来，由此体会数学在足球赛事中的应用。

（5）问题的语言表述尽可能优美、生动、亲切，体现对学生的人文关怀和教育情怀（这也是数学的善的一面）。这样的问题可使学生领略数学文化的美妙、意趣，引导他们亲近数学、理解数学，将来在学习、生活和工作中运用数学。

专家题词：

部分专家、师生在文化节活动中的发言：