《人口论》出版于1798年,作者为英国的托马斯·罗伯特·马尔萨斯牧师(Thomas Robert Malthus,1766年2月13日-1834年12月23日)。
这本书在我的印象中很恐怖,因为一个声音说它是社会达尔文主义,是人种灭绝的理论来源;一个声音说它站在人民的对立面,是反动学说的代表。我今天翻了半天,却没发现什么恐怖的字眼,只看到它是一本经济学的奠基之作,可能比《国富论》更有资格。
总量有限增长
《人口论》关于总量方面核心观点就是人口增长要和资源约束相匹配,前提假设是人口呈几何级数增长,资源呈线性增长。我们用数学模型来表示就是:
1)无限增长模型—指数增长
dN/dt = rN (1.1)
积分后得到:
N(t) = N(0) exp(rt) (1.2)
N——种群密度
r——种群在没有密度制约因素条件下的增长速率,r常被称为“马尔萨斯参数Malthusian parameter”或“内生增长率intrinsic growth rate”
2)有限增长模型—逻辑增长模型
在马尔萨斯的人口论发表40年之后,比利时数学家Pierre François VerhulstVerhulst(1838)用下述数学模型来描述了马尔萨斯的人口理论:
dN/dt=rN(1-N/K) (1.3)
N——种群(人口)密度
r——内生增长率(intrinsic growth rate)
K——环境容量(carrying capacity),决定于食物、空间或其它
r(1-N/K)——
每个个体的增长率
N=K时,种群达到平衡。
将式(1.3)积分后,得到:
N(t)=K/(1+CKe-rt) (1.4)
N(t)——时间t时的个体数
C = 1/N(0)−1/K
Verhulst在其1845年发表的论文中称式(1.4)为逻辑函数(logistic function),现在通常称为逻辑方程式(logistic equation)
。这个模型
发表在达尔文的《物种起源》(1859年)之前,但是
直到1920年,才被Raymond Pearl和LowellReed付诸应用。
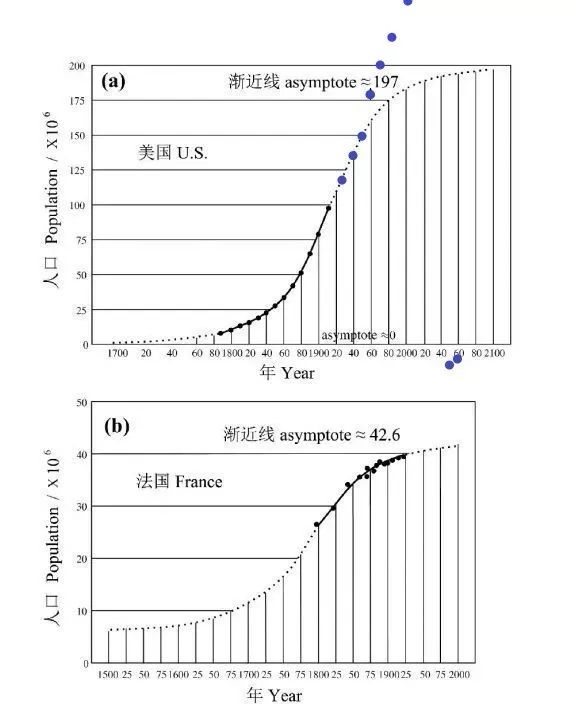
上图为Pearl(1925年)依照上述模型拟合的美国(a)和法国(b)人口数据,结果近乎完美。我们补充后续数据检验,发现美国人口数据在1950年之前,与预测模型有非常好的拟合,之后逐步偏移。原因可能是:1)1950年开始的信息技术和能源化工等领域的技术进步,比以往几轮技术进步更大幅度的扩大了人类的环境容量K;2)模型中r是人口的内生增长率,移民不在估量之内。

结构分化
马尔萨斯生活的时代,欧洲也可以说是千年未有之变局。
三十年宗教战争(1618-1648年)之后,欧洲进入了相对和平时期,并积极开拓海外市场,所以出生率和工资水平双升。马尔萨斯统计了欧洲一些国家1690s-1750s的人口数据,一对夫妇平均生3-5个孩子,出生数和死亡数之比大约在1.5:1。
1750s开始,劳动力供给充足,生育率还在逐渐提高,导致工资水平急剧下滑,大多数人难以生存,便产生了激烈的社会动荡。

经典作品都是对社会现实开出的一剂药方,《人口论》也不例外。
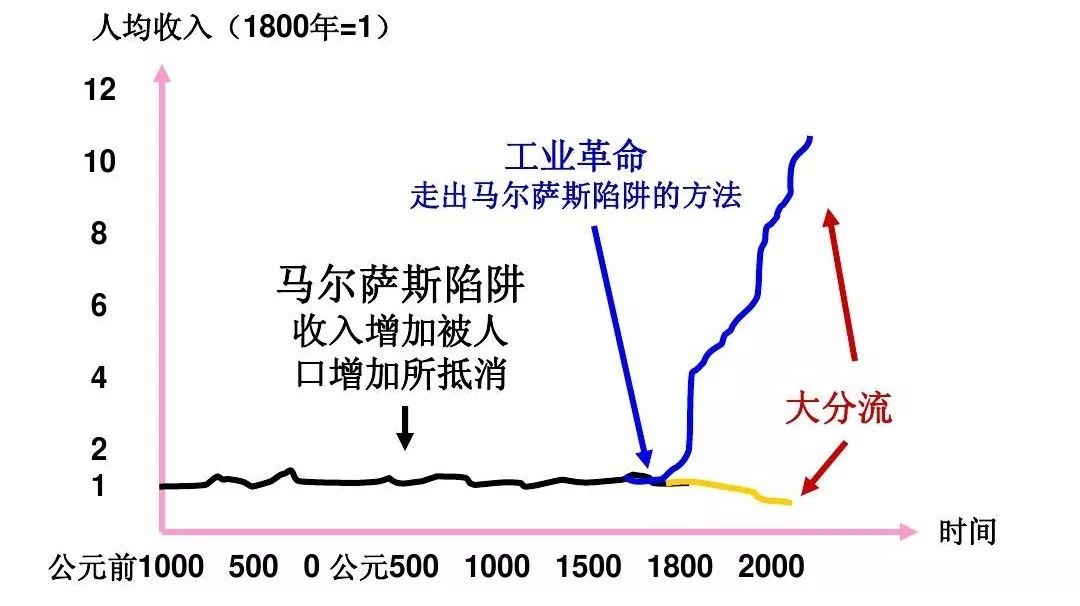
马尔萨斯生活在工业革命方兴未艾的时代,未能预见技术对环境容量的持续开拓,所以给出的对策就是人口“迁就”资源,少生一点
,所以也就诞生了一个词叫马尔萨斯陷阱。现在我们通常说,依靠技术进步才能跳出陷阱,但在当时,这是个不被关注的看法,主流的声音属于革命者。
任何时代的革命者都是满怀理想,口号基本都是人人平等,天下大同,具体做法无外乎打土豪,分田地。但对于当时流行的空想社会主义(当时倡议者可不同意这个名词,嘿嘿~~),马尔萨斯保持了一份现实和理性。
他认为,人人都得到一样多的资产,穷人生活得到改善,结果就是会出生更多的人口,这样就又回到了很多人吃不饱的原点。所以,空想社会主义注定是一个不可能实现的理想。
同时代还有一个大神——亚当斯密(1723—1790年),说二次分配呀,设立供养劳动者基金,社会收入或者资本的一切增加都可以增加这个基金。马尔萨斯则认为,工业财富的增加,并不能相应的转化为食物,无助于改善穷人的状况。这句放在当下,相当于说金融财富的增加(比如房子,股票涨了),无助于改善没钱人的状况。
英国当时正处于蒸蒸日上的阶段,但事实上,
供养劳动者基金并未增加,英国穷人的致富还是靠亚非拉人民的“帮衬”。难怪有的书说,亚当斯密的发财致富之路,就是教别人如何发财致富,O(∩_∩)O哈哈~
现在我们也经常听各路神仙告诉我们,说经济发展穷人受益更多,普通人的日子比皇帝还好。但是,穷人和富人是相对概念,互为存在前提,讨论二者相对关系在时间上的变化,比单独讨论其一更有意义。如果“穷人”过得越来越好,法国也不会一会儿黄马甲游行,一会儿工会组织罢工了。